Introduction To The Probability

25 May 2018

Prologue To Introduction To The Probability

The probability describes how likely it is the test takes place with the expected result. It is the fundamental for modern world science.

Begin From The Fundamental

[1] sample space

➀sample space is just the set of elements describing the outcomes of the test, experiment, formally, the result after execution of certain action.
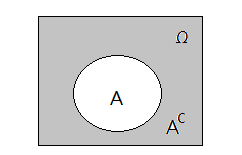
In statistics reference text book, the letter $\Omega$ is most often used to represent the sample space.
➁by flipping a coin one time, you will have two outcomes of head and tail, that is to say we associate the sample space with the set $\Omega$=$\{H,T\}$.
➂to guess the birthday within one week, the sample space $\Omega$=$\{Sun,Mon,Tue,Wed,Thu,Fri,Sat\}$.

[2] event

➀subset of a sample space is treated as event.
➁in the birthday in one week example, suppose we’d like to ask for the days with uppercase “S” as the prefix, then, we can denote $S$=$\{Sun,Sat\}$.
➂suppose we’d like to ask for the days with uppercase “T” as the prefix, then, we can denote $T$=$\{Tue,Thu\}$.

[3] intersection, union, complement

Suppose $A$ and $B$ are two events in the sample space $\Omega$.
➀intersection, it’s an event operator, denoted by $\cap$.
➁union, also an event operator, denoted by $\cup$.
➁complement, an event operator, usually denoted by lowercase $c$.

[4] disjoint events

Suppose $A$ and $B$ are two events in the sample space $\Omega$. They are said to be two disjoint events if they have no intersection. $A\cap B$=$0$.
Such events might be regarded as mutually exclusive.

The Probability

[1] why do we need the probability?

In order to express how likely it is that an event will occur, during the experiment, by assigning probability to each distinct event would be common. To distribute the probability accurately would not be an easy task.

[2] the probability function

Since each event would be associated with a probability, then we are in need of the probability function.
➀the uppercase “P” is the probability function on a sample space $\Omega$ to assign the event $A$ in $\Omega$ a number $P(A)$ in $[0,1]$. The number $P(A)$ is the probability of the occurrence of event $A$.
➁wherein $P(\Omega)$=$1$
➂$P(A\cup B)$=$P(A)$+$P(B)$-$P(A\cap B)$, where $P(A\cap B)$=$0$ for $A$ and $B$ are disjoint. If $A$,$B$,$C$ are disjoint events, then $P(A\cup B\cup C)$=$P(A)$+$P(B)$+$P(C)$.

[3] the probability is defined on events, not on outcomes

➀tossing a coin one time would we have $\Omega$=$\{H,T\}$, then $P(\{H\})$=$\frac {1}{2}$, $P(\{T\})$=$\frac {1}{2}$, under the assumption that head and tail chances are coming to an equilibrium.
➁given cards of read, blue, green colours. The permutation of all the possible orders of cards would be $\Omega$=$\{RGB$,$RBG$,$GRB$,$GBR$,$BRG$,$BGR\}$.
$P(\{RGB\})$=$P(\{RBG\})$=$P(\{GRB\})$=$P(\{GBR\})$=$P(\{BRG\})$=$P(\{BGR\})$=$\frac {1}{6}$…the same probability for each distinct event.
➂the same example as above, the probability of the event that green card is in the middle would be $P(\{RGB,BGR\})$=$\frac {1}{3}$.
The $\{RGB,BGR\}$ is such event we desire, wherein the $\{RGB\}$ and $\{BGR\}$ are the outcomes described by $\Omega$.

[4] additivity of probability

➀using the same card example, the probability of the event that green card is in the middle could be $P(\{XGX\})$=$P(\{RGB\})$+$P(\{BGR\})$=$\frac {1}{3}$.
This implies that the probability of an event could be obtained by summing over the probabilities of the outcomes belonging to the same event.
➁given $A$ is an event, then $P(A)$+$P(A^{c})$=$P(\Omega)$=$1$.
➂if $A$, $B$ are not disjoint, then $A$=$(A\cap B)\cup(A\cap B^{c})$, this is a disjoint union.
Therefore, $P(A)$=$P(A\cap B)$+$P(A\cap B^{c})$.

Product Of Sample Space

[1] run the same test over multiple times

To justify the experiment result, one single test would be executed over multiple times.
➀suppose we flip the same coin over 2 times, the sample space $\Omega$=$\{H,T\}$x$\{H,T\}$.
It is now $\Omega$=$\{HH,HT,TH,TT\}$. Total 4 outcomes in it, we can take one outcome as one event, then $P(\{HH\})$=$P(\{HT\})$=$P(\{TH\})$=$P(\{TT\})$=$\frac {1}{4}$, under the assumption that $P(\{H\})$=$P(\{T\})$ in each single tossing of coin.

[2] combine the sample space from different tests

➀given that 2 sample spaces with respect to 2 different tests’ outcomes, they are $\Omega_{1}$,$\Omega_{2}$, where sizeof($\Omega_{1}$)=$r$, sizeof($\Omega_{2}$)=$s$.
➁then $\Omega$=$\Omega_{1}$x$\Omega_{2}$, sizeof($\Omega$)=$r\cdot s$. If we treat each distinct combination in the sample space as one single event, the probability of such distinct event is $\frac {1}{r\cdot s}$. The $\frac {1}{r}$,$\frac {1}{s}$ are the probability for the occurrences of outcomes in the $\Omega_{1}$ and $\Omega_{2}$ with respect to test 1 and test 2.

[3] general form of the same test over multiple times

➀suppose we’d like to make the experiment for n runs. We take $\Omega_{i}$ to be the sample space of the i-th test result, $\omega_{i}$ to be one of the outcomes in $\Omega_{i}$.
➁if the occurrence of each outcome $\omega_{i}$ has probability $p_{i}$, then $P(\{\omega_{1},\omega_{2}…\omega_{n}\})$=$p_{1}\cdot p_{2}…p_{n}$, which is the probability for the event $\{\omega_{1},\omega_{2}…\omega_{n}\}$ to take place.
➂assume we flip a coin with probability $p$ of head, that implies $1-p$ of tail. Then the probability of 1 single head after 4 times of tossing would be $4\cdot (1-p)^3\cdot p$.
The sample space would be
$\Omega$=$\{(HTTT),(THTT),(TTHT),(TTTH)\}$. There are 4 combinations, with each has probability $(1-p)^{3}\cdot p$.

An Infinite Sample Space

[1] run the same test until succeeds

➀suppose we’d like to toss a coin until it appears with head. If the tail is always the result, the sample space $\Omega$=$\{T_{1},T_{2},T_{3},…,T_{n}…\}$, $n\rightarrow\infty$.
Next to ask the probability function of this sample space. Assume the probability of head is $p$, the tail is $1-p$.

[2] run the same test until succeeds

➀for the simplicity, we’d like to change the notation by $\Omega$=$\{1,2,..,n,…\}$ for the number of iterations the tossing coin result coming out with a head.
➁$P(1)$=$P(\{H\})$=$p$
➂$P(2)$=$P(\{TH\})$=$(1-p)\cdot p$
➃$P(n)$=$P(\{T_{1}T_{2}…T_{n-1}H_{n}\})$=$(1-p)^{n-1}\cdot p$
➄when $a$ is incredibly large, the total probability becomes
$\lim_{n\rightarrow\infty}P(1)+P(2)+…+P(n)$
=$\lim_{n\rightarrow\infty}p+(1-p)\cdot p+…+(1-p)^{n-1}\cdot p$
=$\lim_{n\rightarrow\infty}p\cdot\frac {1}{1-(1-p)}$
=$p\cdot\frac {1}{p}$
=$1$…the total probability

In an infinite sample space, if all the events $A_{1}$,$A_{2}$,…,$A_{n}$ are disjoint, then,
$P(\Omega)$
=$P(A_{1}\cup A_{2}\cup…\cup A_{n})$
=$P(A_{1})$+$P(A_{2})$+…$P(A_{n})$
=$1$