The Bayes Theorem Significance

28 May 2018

Prologue To The Bayes Theorem Significance

The most optimized effect of Bayes theorem is to use already known probability to figure out the maximum unknown probability in its likelihood, instead of manual counting in the sample space. The Bayes theorem is the weapon for quantitative critical thinking to overcome the drawback of qualitative thinking of human nature.

The Bayes Theorem Significance

$\;\;\;\;P(B_{i}\vert A)$=$\frac {P(A\vert B_{i})\cdot P(B_{i})}{P(A\vert B_{1})\cdot P(B_{1})+…+P(A\vert B_{n})\cdot P(B_{n})}$

[1] The general form of Bayes theorem embedes a total probability expression in its denominator part.

➀such total probability is the linear combination of the events in the sample space with the probability $P(A\vert B_{i})$, the occurrence of the target condition $A$, under the given partitioned sample space $B_{i}$ as it’s weighting.
➁usually, $A$ is the qualitative feature of interest.
➂$\Omega$=$\{B_{1},B_{2},…,B_{n}\}$, where $B_{i}$ is the partition os the sample space.

[2] The general form of Bayes theorem has joint probability expression in its nominator part.

➀the joint probability is expressed in terms of $P(A\vert B_{i})\cdot P(B_{i})$.
➁$P(A\vert B_{i})\cdot P(B_{i})$=$P(A\cap B_{i})$, is to calculate the possible likelihood of the probability of the coexistence of $A$ and $B_{i}$.

[3] Take the Bayes theorem into parts

There exists 4 factors in the Bayes theorem expression.
➀$B_{i}$ is the prior probability, the already known probability.
➁$P(A\vert B_{i})$ is the likelihood function, by intuition the qualitative term, its major effect is the estimation of the possible likely probability of the occurrence of target event of interest $A$, under the given condition/partition $B_{i}$ of sample space.
➂the total probability also called the marginal probability, it is the summation over the distribution of each distinct $B_{i}$ with regards to the specific $A$, that means there could be infinite numbers of $A$.
➃$P(B_{i}\vert A)$ is the posterior probability, by intuition the quantitative target, now the sample space is the target event of interest $A$.

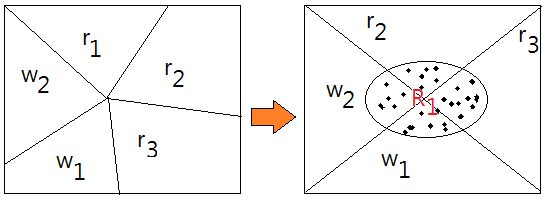
Example: 3 Red And 2 White Balls

[Question]

Given that there are 3 red and 2 white balls in a bow. Suppose you pick up 2 balls sequentially. What’s the probability of picking up the 2nd white ball and the 1st one is the red ball?

[Answer]

This is asking for $P(W_{2}\cap R_{1})$. Denote $R_{i}$,$W_{i}$ as the i-th picking the red, white ball up.
➀when we pick up the very first ball, $\Omega$=$\{r_{1},r_{2},r_{3},w_{1},w_{2}\}$.
$P(R_{1})$=$\frac {3}{5}$, the probability that the 1st ball is a red ball.
➁when we pick up the second ball, $\Omega$=$\{r_{2},r_{3},w_{1},w_{2}\}$.
$P(W_{2}\vert R_{1})$=$\frac {2}{4}$, the probability that the 2nd ball is a white ball, given that the first one is the red ball.
➂$P(W_{2}\cap R_{1})$=$P(W_{2}\vert R_{1})\cdot P(R_{1})$=$\frac {6}{20}$.

[More details]

➀$P(R_{1})$ is the prior priority.
➁$P(W_{2}\vert R_{1})$ is the likelihood function to estimate the probability that the 2nd ball is a white ball, given that the first one is the red ball.
➂$P(W_{2}\vert R_{1})\cdot P(R_{1})$ is the joint probability of the coexistence of $W_{2}$ and $R_{1}$, since we are asking for the probability of picking up the 2nd white ball and the 1st one is the red ball.

Example: quantitative versus qualitative::mjtsai1974

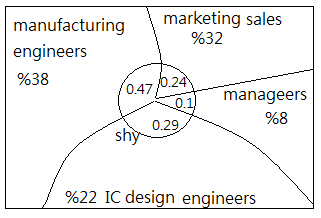
[Question]

Suppose the statistical population distribution in the Hsin-Chu science park area reports that $\%8$ of the population is the managers, $\%32$ is the marketing sales, $\%38$ is the manufacturing engineers, $\%22$ is the IC design engineers.
Given that Albert is a man, when you see him, his behavior is a little shy, talktive with strangers for road seeking, and is not talktive in political topics.

According to recent statistical research that given a manager, $0.1$ probability being shy; given a marketing sales, $0.24$ probability being shy; given a manufacturing engineer, $0.47$ probability being shy; given an IC design engineer, %0.29% probability being shy.

Under such condition, given that Albert is a shy man, what kind of identity has the maximum probability?

[Answer]

➀take $P(Mgr)$=$0.08$, $P(Sales)$=$0.32$, $P(M_{eng})$=$0.38$, $P(I_{eng})$=$0.22$ for probability of being managers, marketing sales, manufacture engineers, IC design engineers, which are all the prior probability.
➁take $P(Shy\vert Mgr)$=$0.1$, $P(Shy\vert Sales)$=$0.24$, $P(Shy\vert M_{eng})$=$0.47$, $P(Shy\vert I_{eng})$=$0.29$ for given a manager, a marketing sales, a manufacturing engineer, IC design engineer, the probability being shy respectively, which are all the likelihood function, the qualitative term.
➂the question asks for the maximum in between $P(Mgr\vert Shy)$, $P(Sales\vert Shy)$, $P(M_{eng}\vert Shy)$, $P(I_{eng}\vert Shy)$. Trivially, we need the total probability of being shy.
$P(Shy)$
=$P(Shy\vert Mgr)\cdot P(Mgr)$+
$\;\;\;\;P(Shy\vert Sales)\cdot P(Sales)$+
$\;\;\;\;P(Shy\vert M_{eng})\cdot P(M_{eng})$+
$\;\;\;\;P(Shy\vert I_{eng})\cdot P(I_{eng})$
=$0.1\cdot 0.08$+$0.24\cdot 0.32$+$0.47\cdot 0.38$+$0.29\cdot 0.22$
=$0.3272$
➃finally, the posterior probability:
$P(Mgr\vert Shy)$=$\frac {P(Shy\vert Mgr)\cdot P(Mgr)}{P(Shy)}$=$\frac {0.1\cdot 0.08}{0.3272}$=$0.0244$
$P(Sales\vert Shy)$=$\frac {P(Shy\vert Sales)\cdot P(Sales)}{P(Shy)}$=$\frac {0.24\cdot 0.32}{0.3272}$=$0.2347$
$P(M_{eng}\vert Shy)$=$\frac {P(Shy\vert M_{eng})\cdot P(M_{eng})}{P(Shy)}$=$\frac {0.47\cdot 0.38}{0.3272}$=$0.5458$
$P(I_{eng}\vert Shy)$=$\frac {P(Shy\vert I_{eng})\cdot P(I_{eng})}{P(Shy)}$=$\frac {0.29\cdot 0.22}{0.3272}$=$0.1949$

By means of quantitative posterior, we found that $P(M_{eng}\vert Shy)$ has the largest posterior probability and implies the maximum possibility that Albert is a shy man, he is a manufacture engineer.