The Bayesian Inference Exploitation

17 Jun 2018

Prologue To The Bayesian Inference Exploitation

Bayesian inference is resembling gradient descendent approach to guide the experiment to the target satisfication, they are not the same, but alike!

Prepare to Exploit The Bayesian Inference

[1] ReCap The bayesian inference

We can characterize how one’s beliefs ought to change when new information is gained.

Remember the illustration example in the The Bayesian Thinking, I have show you by contiguous update the given prior by the estimated posterior would we obtain the desired result by reinforcement.

[2] The question in mind

From #1, #2, #3 tests, by feeding the prior with the positive posterior estimation, then we get almost $100\%$ in $P(Cancer\vert Malignant)$. Below are the unknowns:
➀how, if we update the given prior several times with the positive posterior estimation, $P(Cancer\vert Malignant)$, laterly make contiguous negative posterior estimation, $P(Cancer\vert Benign)$?
➁will we have the chance to increase the negative posterior estimation, in its probability, $P(Cancer\vert Benign)$?
➂for the answer of yes and no, could we describe the exact trend of $P(Cancer\vert Benign)$?
➃or, is there some condition far beyond our naive beliefs that prior updated by some amount of positive posterior, we can concrete the negative posterior?

[3] The stress test

Below is my stress test flow:
➀the rule of updating prior by the estimated posterior remains the same, when we make estimation of $P(Cancer\vert Malignant)$ and $P(Cancer\vert Benigh)$, at the end of each test, we do the update job.
➁by executing $P(Cancer\vert Malignant)$ in $i$ times, next to execute $P(Cancer\vert Benign)$ over $100-i$, where $i$=$1$ to $100$.
➂below graph exhibits the result of $P(Cancer\vert Malignant)$x${i}$, $P(Cancer\vert Benign)$x$(100-i)$ for the first 12 tests:
The results are depicting from the left, top to the right, low in orders. For the simplicity, I denote $P(C\vert T)$ as $P(Cancer\vert Malignant)$, $P(Cancer\vert F)$ as $P(Cancer\vert Benign)$.
➃trivially, $P(C\vert T)$x$9$ to $P(C\vert T)$x$10$ is the major point, after positive posterior over $10$ times, the following negative posterior won't be decreased, and keeps the same result as the latest positive posterior!

Exploit The Bayesian Inference

Next we investigate what positive posterior over $10$ times has put inside the whole process, such that the following up $90$ negative posteriors would not downgrade the probabilistity of $P(Cancer\vert Benigh)$.

[1]By comparing the statistical log info of $P(C\vert T)$x$9$ and $P(C\vert T)$x$10$
The test is 0-index based in my log, so you see run 9 is actually the 10-th execution of the test:
➀the log comparison reveals that the run #9 in $P(C\vert T)$x$9$, the left side, says $P(Cancer\vert Benign)$ is almost $1$, but not yet!
➁the right side result, the run #9 in $P(C\vert T)$x$10$ says $P(Cancer\vert Malignant)$ is equivalent to $1$!
➂the left side $P(C\vert F)$x$9$ has its $P(Cancer)$ and the total probability of $P(Malignant)$ downgraded, since the negative posterior is thus estimated:
$P(Cancer\vert Benign)$=$\frac {P(Benign\vert Cancer)\cdot P(Cancer)}{P(Benign)}$
$P(Benign)$=$P(Benign\vert Cancer)\cdot P(Cancer)$
$\;\;\;\;$+$P(Benign\vert Free)\cdot P(Free)$

The $P(Free)$ and $P(Benign)$ are compounded slowly increasing, the root cause to gradually decrease $P(Cancer\vert Benign)$!!

➃the right side $P(C\vert T)$x$10$, from the run #9(10-th) test of $P(Cancer\vert Malignant)$, we have $P(Cancer)$=$1$, $P(Free)$=$0$ keep invariant change in the total probability of $P(Malignant)$ and $P(Benign)$.
➄continue to inspect the log comparison result, we can see that in the series of $P(C\vert T)$x$9$, $P(C\vert F)$x$91$, the negative posterior becomes smaller and finally to 0; nevertheless, the $P(C\vert T)$x$10$, $P(C\vert F)$x$90$, we have $P(Cancer\vert Benign)$=$1$ all the way to the test end.

[2]Deeper inside $P(C\vert T)$x$9$ and $P(C\vert T)$x$10$
To make my findings concrete, the statistical summary of the 2 series are given in below graphs:
➀below graph illustrates the consistency of my finding is of no doubt in $P(C\vert T)$x$9$.
➁the same in $P(C\vert T)$x$10$.

[3]Other testing reports
At the end of this article, I depict all stress test I have done.
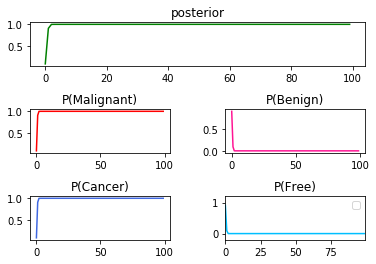
➀it is the result of $P(Cancer\vert Malignant)$x$100$:
➁it is the result of $P(Cancer\vert Benign)$x$100$:
➂below exhibits the result in the series $P(Cancer\vert Malignant)$x$50$, then $P(Cancer\vert Benign)$x$50$:
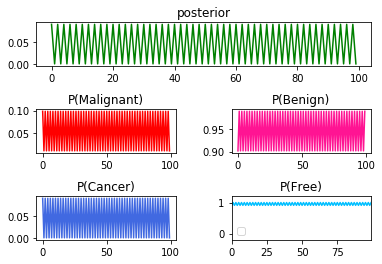
➃the result in the series $P(Cancer\vert Malignant)$,then $P(Cancer\vert Benign)$ as a whole the pattern for the behavior in the rest process:
You can tell that the patterned toggling exist for all terms of probability.

All above reports are generated by my Python simulator. The related logs are downloaded here, $P(Cancer\vert Malignant)$ over $9$ times and $P(Cancer\vert Malignant)$ over $10$ times.