Variable Elimination In Bayesian Network
15 Jul 2018Prologue To Variable Elimination In Bayesian Network
Inference Via Bayesian Network
Given a well-constructed BN of nodes, 2 types of inference are supported:
➀predictive support(top-down reasoning) with the evidence nodes connected to node $X$, through its parent nodes, the same direction as predictive propagation.
➁diagnostic support(bottom-up reasoning), with vidence nodes connected to node $X$, through its children nodes, the same direction as retrospective propagation.In my Bayesian articles, I have guided you through both types of support by means of variable enumeration over the factorized terms of full joint PDF(probability distribution function). Most of the examples are all in small network, trivially, variable enumeration is old, she will hold for complex model consisting of a lot random variables, resulting in high expenditure of computation efficiency. Therefore, another technique of variable elimination is introduced.
Example: Illustration Of Variable Elimination
This example is simplified from variable elimination, Peter Norvig.
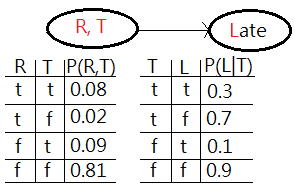
[Question]Suppose you are using a Bayesian network to infer the relationship in between raining, traffic and late(to office). The probability of raining and the conditional probability of traffic jam, given raining, and being late, given traffic jam are all depicted in this graph. What’s the probability of being late?
[Answer]
This is to ask for $P(L=t)$. The full joint PDF would be $P(R,T,L)$=$P(L\vert T)\cdot P(T\vert R)\cdot P(R)$.
By the old variable enumeration, $P(L=t)$=$\sum_{R}\sum_{T}P(R,T,L=t)$, the nested summation over $T$ would be proceeded inside the outer summation over $R$. Here, we’d like to further reduce the computation complexity by means of variable elimination.
[1]The first would be to join factors:
➀a factor is one of these tables of probability, $P(R)$, or the conditional probability, $P(T\vert R)$, $P(L\vert T)$. By usual, they are multi-dimensional matrix.
➁what we do is to choose 2 or more of these factors. In this case, we choose $P(R)$ and $P(T\vert R)$, to combine them together to form a new factor which represents the joint probability of all variables, $R$ and $T$ in that new factor $P(R,T)$.
➂we perform the operation of joining factors on these 2 factors, $P(R)$, $P(T\vert R)$, getting a new factor which is part of the existing network. Below exhibits what we have now.
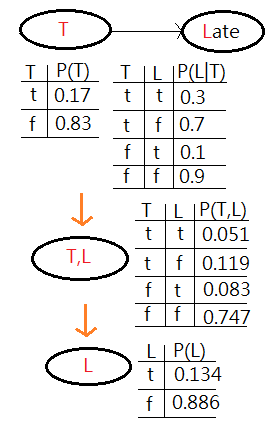
[2]The second is the operation of elimination, also called summing out or marginalization, to take the table $P(R,T)$, reduce it to $P(T)$, finally combine it with $P(L\vert T)$ to get $P(L)$.
➀by now, we sum out or marginalize $P(R,T)$ over the variable $R$ to get $P(T)$ that just operates on $T$. That is what we have in the network, by summing out over all values of $R$, respectively for which $T=t$ and $T=f$.
➁next, we do a join over $T$ and $L$, by combining $P(T)$ and $P(L\vert T)$ to get a new factor of joint probability $P(T,L)$.
➂now, we are down to a network with a single node, $T,L$ with the joint probability table. By summing out $P(T,L)$ over $T$ with respect for $L=t$ and $L=f$, finally we reach the single node $L$ with $P(L=t)$ and $P(L=f)$.
It is a continued process of joining together factors to form a maybe larger factor and then eliminating variables by summing out(marginalization).
Optimal Order For Variable Elimination Is NP-Hard
In this paragrapg, I’d like to illustrate the execution of different elimination order would probabilistically result in computational side effect. I’m going to use an example from Prof. Abbeel, steps through a few variable examples, but with my own viewpoint.
[Question]The given BN is depicted below, what’s $P(U\vert +z)$?
[Order: $X$,$Y$,$V$,$W$]
We are initialized with these factors, they are $P(U)$,$P(V)$,$P(W)$,$P(X\vert U,V)$,$P(Y\vert V,W)$,$P(Z\vert X,Y)$. Asking for $P(U\vert +z)$ is to eliminate the nodes of $X$,$Y$,$V$,$W$ in the network.
➀do the factor join over $X$ to eliminate $X$:
[Order: $V$,$W$,$X$,$Y$]
$f_{1}(+z,Y,U,V)$=$\sum_{x}P(+z\vert x,Y)\cdot P(x\vert U,V)$
There is a finding that the elimination of the node with multiple parents would generate a new factor with the number of extra added variables eqivalent to the number of its parents.
➁do the factor join over $Y$ to eliminate $Y$:
$f_{2}(+z,U,V,W)$=$\sum_{y}f_{1}(+z,y,U,V)\cdot P(y\vert V,W)$
➂do the factor join over $V$ to eliminate $V$:
$f_{3}(+z,U,W)$=$\sum_{v}f_{2}(+z,U,V,W)\cdot P(v)$
➃do the factor join over $W$ to eliminate $W$:
$f_{4}(+z,U)$=$\sum_{w}f_{3}(+z,U,W)\cdot P(w)$
➄we are left with $f_{4}(+z,U)$ and $P(U)$, then:
$P(U\vert +z)$=$\frac {P(U\cap +z)}{P(+z)}$, where $P(+z)$=$\sum_{u}f_{4}(+z,u)$ and $P(U\cap +z)$=$\sum_{u}f_{4}(+z,u)\cdot P(u)$. Be noted that this description won’t be repeated in below sections.
➅we can examine each new generated facor, inspect its scale, the width. Below exhibits each distinct generated factor’s number of variables.
The maximum number in the new generated factor is 3, is such order the most optimal? Let’s continue to walk it through.
➀do the factor join over $V$ to eliminate $V$:
[Order: $W$,$V$,$Y$,$X$]
$f_{1}(X,U,Y,W)$=$\sum_{v}P(X\vert U,V)\cdot P(Y\vert V,W)\cdot P(V)$
There is another finding that the elimination of a node having more multiple children, then these children and their parents(if any), must be taken into computation cost.
➁do the factor join over $W$ to eliminate $W$:
$f_{2}(X,U,Y)$=$\sum_{w}f_{1}(X,U,Y,w)\cdot p(w)$
➂do the factor join over $X$ to eliminate $X$:
$f_{3}(+z,U,Y)$=$\sum_{x}f_{2}(X,U,Y)\cdot P(+z\vert x,Y)$
➃do the factor join over $Y$ to eliminate $Y$:
$f_{4}(+z,U)$=$\sum_{y}f_{3}(+z,U,y)$
➄you can follow [Order: $X$,$Y$,$V$,$W$]’s approach to renomalize for the answer.
➅we then examine each new generated facor, inspect its scale, the width. Below exhibits each distinct generated factor’s number of variables.
The maximum number in the new generated factor is 4, this elimination order is worse than $X$,$Y$,$V$,$W$ in computation efficiency. Let’s continue to walk it through to see if we can find another better one.
➀do the factor join over $W$ to eliminate $W$:
[Order: $W$,$Y$,$V$,$X$]
$f_{1}(Y,V)$=$\sum_{w}P(Y\vert V,w)\cdot P(w)$
➁do the factor join over $V$ to eliminate $V$:
$f_{2}(Y,X,U)$=$\sum_{v}f_{1}(Y,v)\cdot P(X\vert U,v)\cdot P(v)$
This is the same finding that the elimination of a node having more multiple children, then these children and their parents(if any), must be taken into computation cost.
➂do the factor join over $Y$ to eliminate $Y$:
$f_{3}(+z,X,U)$=$\sum_{y}f_{2}(y,X,U)\cdot P(+z\vert X,y)$
➃do the factor join over $X$ to eliminate $X$:
$f_{4}(+z,U)$=$\sum_{x}f_{3}(+z,X,U)$
➄you can follow [Order: $X$,$Y$,$V$,$W$]’s approach to renomalize for the answer.
➅we then examine each new generated facor, inspect its scale, the width. Below exhibits each distinct generated factor’s number of variables.
The maximum number in the new generated factor is 3, this elimination order is much betten than $V$,$W$,$X$,$Y$ in computation efficiency, and little better than $X$,$Y$,$V$,$W$. Let’s continue to walk it through to see if we can find another better one.
➀do the factor join over $W$ to eliminate $W$:
[Order: $W$,$Y$,$X$,$V$]
$f_{1}(Y,V)$=$\sum_{w}P(Y\vert V,w)\cdot P(w)$
➁do the factor join over $Y$ to eliminate $Y$:
$f_{2}(+z,X,V)$=$\sum_{y}f_{1}(y,V)\cdot P(+z\vert X,y)$
➂do the factor join over $V$ to eliminate $V$:
$f_{3}(+z,X,U)$=$\sum_{v}f_{2}(+z,X,v)\cdot P(X\vert U,v)\cdot P(v)$
➃do the factor join over $X$ to eliminate $X$:
$f_{4}(+z,U)$=$\sum_{x}f_{3}(+z,X,U)$
➄you can follow [Order: $X$,$Y$,$V$,$W$]’s approach to renomalize for the answer.
➅we then examine each new generated facor, inspect its scale, the width. Below exhibits each distinct generated factor’s number of variables.
The maximum number in the new generated factor is 2, this elimination order is much betten than all previous orders. Let’s continue one more to see if we can find another better one.
➀do the factor join over $W$ to eliminate $W$:
$f_{1}(Y,V)$=$\sum_{w}P(Y\vert V,w)\cdot P(w)$
➁do the factor join over $Y$ to eliminate $Y$:
$f_{2}(+z,X,V)$=$\sum_{y}f_{1}(y,V)\cdot P(+z\vert X,y)$
➂do the factor join over $X$ to eliminate $X$:
$f_{3}(+z,U,V)$=$\sum_{x}f_{2}(+z,X,V)\cdot P(x\vert U,V)$
➃do the factor join over $V$ to eliminate $V$:
$f_{4}(+z,U)$=$\sum_{v}f_{3}(+z,U,V)\cdot P(v)$
➄you can follow [Order: $X$,$Y$,$V$,$W$]’s approach to renomalize for the answer.
➅we then examine each new generated facor, inspect its scale, the width. Below exhibits each distinct generated factor’s number of variables.
The maximum number in the new generated factor is 2, this elimination order is the same good as $W$,$Y$,$V$,$X$, much betten than all other orders. There exists total $4\cdot 3\cdot 2\cdot 1$ combinations.
So far, we reduce the scale(width) to 2 variables in the new generated factor should be confident to stop, since there should exist no factor ocntaining only 1 variable in this case!!
[Conclusion]➀if we make the good choice of the order in which we apply these operations, then variable elimination can be much more efficient than just doing the whole enumeration!!
➁it’s an NP-hard issue to find an optimal order for variable elimination.
Variable Elimination Order Heuristics
The following heuristics are not the final solution to the most optimal order of variable elimination:
➀choose the variable with the fewest dependent variables.
➁choose the variable to minimize the product of cardinalities of its dependent or related variables.
➂choose the vertices to minimize the size of factors to be added in the graph.
Resort to related papers, textbooks, online references, I’d like to follow up Variable elimination, CS228, Stefano Ermon, instead of the complicated algorithm description and implementation here, since they are not jargon-free, you are welcome to my future article.
Addendum
➀Prof. Abbeel, steps through a few variable examples
➁Variable elimination, Peter Norvig
➂Bayesian Networks, Ben-Gal Irad, in Ruggeri F., Faltin F. & Kenett R., Encyclopedia of Statistics in Quality & Reliability, Wiley & Sons (2007).
➃Variable elimination, CS228, Stefano Ermon