Propagation In The Bayesian Network

26 Aug 2018

Prologue To Propagation In The Bayesian Network

The respective and retrospective inferences ascertained by means of variable elimination is also computation expensive, it works for one variable at a time, the same operation would be repeated upon new inference on other variables is requested. An alternative to overcome these limitations is by using propagation in the Bayesian network.

Posterior Probability(Belief) Update Upon New Evidence Arrives

[1] Posterior probability(belief)

The posterior probability(belief) of a random variable $X$=$x$, given evidence $E$=$e$, is expressed as $Bel(x)\overset\triangle=P(x\vert e)$. The evidence could be further classified as 2 distinct subsets:
➀$e_{X}^{-}$ denotes the evidence introduced through its children nodes.
➁$e_{X}^{+}$ stands for the evidence coming from its parent nodes, for $X$ to be a root node, $e_{X}^{+}$ is the background.

[2] Deduction of $Bel(x)$

Assume $e_{X}^{-}$ and $e_{X}^{+}$ are independent, then the belief of $X$=$x$:
$Bel(x)$
=$P(x\vert e_{X}^{-},e_{X}^{+})$
=$\frac {P(e_{X}^{-},x\vert e_{X}^{+})}{P(e_{X}^{-}\vert e_{X}^{+})}$
=$\frac {P(e_{X}^{-}\vert x,e_{X}^{+})\cdot P(x\vert e_{X}^{+})}{P(e_{X}^{-}\vert e_{X}^{+})}$
=$\frac {P(e_{X}^{-}\vert x)\cdot P(x\vert e_{X}^{+})}{P(e_{X}^{-})}$

Why we have such deduction?
➀the evidence $e_{X}^{-}$ is given by hypothesis $X$=$x$, and the background context $e_{X}^{+}$, that explains $P(e_{X}^{-}\vert x,e_{X}^{+})$.
➁$P(x\vert e_{X}^{+})$ says that the hypothesis $X$=$x$ is propagated from the background context $e_{X}^{+}$.
➂the normalizing factor $P(e_{X}^{-}\vert e_{X}^{+})$ encompasses everything ranging from the background context to the final observed evidence, since $e_{X}^{-}$ and $e_{X}^{+}$ are independent, the denominator part becomes $P(e_{X}^{-})$.
$P(e_{X}^{-})$
=$P(e_{X}^{-}\vert e_{X}^{+})$
=$P(e_{X}^{-}\vert x,e_{X}^{+})\cdot P(x\vert e_{X}^{+})$
=$P(e_{X}^{-}\vert x)\cdot P(x\vert e_{X}^{+})$
=$\lambda(X)\cdot\pi(X)$

[3] Generalization of $Bel(x)$

Most of the textbooks have below common definition:
➀$\pi(x)$=$P(x\vert e_{X}^{+})$ is the respective(predictive) direction of propagation.
➁$\lambda(x)$=$P(e_{X}^{-}\vert x)$ is retrospective(diagnostic) direction of propagation.

We thus express the belief of $x$ as $Bel(x)$=$\alpha\cdot\pi(x)\cdot\lambda(x)$,
where $\alpha$ is the normalizing constant, in this illustration,
$\alpha$
=$[P(e_{X}^{-})]^{-1}$
=$[\sum_{x}\pi(x)\cdot\lambda(x)]^{-1}$

[4] Message passing is propagation

New evidence enters a network when a variable is instantiated, ie when it receives a new value from the outside world. When this happens, the posterior probability of each node in the whole network must be re-calculated.

This is achieved by message passing, known as progapation.

Propagation Illustration In Causal Tree

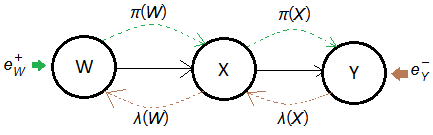
Given a causal tree of this serial chain Bayesian network, where $\lambda(Y)$=$P(e_{Y}^{-}\vert Y)$.

[1] Forward propagation

➀$W$ is now the root node, the background context is the only forward propagated evidence.
$\pi(w)$=$P(w\vert e_{W}^{+})$=$P(w)$, for $w\in W$.
➁for node $X$, it receives the forward propagated evidence pass through it, thus:
$\pi(x)$
=$P(x\vert e_{X}^{+})$
=$P(x\vert e_{WX}^{+})$
=$\sum_{w}P(x\vert w)\cdot P(w\vert e_{W}^{+})$, for $w\in W$.
$\Rightarrow\pi(X)$=$P(X\vert W)\cdot\pi(W)$

Node $X$ receives $W$ forward propagated evidence $P(w\vert e_{W}^{+})$, with each $X=x$ weighted by $P(x\vert w)$ for all $w\in W$.

➂similarly, $\pi(Y)$=$P(Y\vert X)\cdot\pi(X)$

[2] Backward propagation

➀$Y$ is the leaf node, the evidence of observation is the only backward propagated message.
$\lambda(y)$=$P(e_{Y}^{-}\vert y)$
➁as $X$ receives the backward propagated evidence from $Y$, then:
$\lambda(x)$
=$P(e_{X}^{-}\vert x)$
=$P(e_{XY}^{-}\vert x)$
=$\sum_{y}P(y\vert x)\cdot\lambda(y)$, for $y\in Y$.
$\Rightarrow\lambda(X)$=$P(Y\vert X)\cdot\lambda(Y)$

For each $x\in X$, $\lambda(x)$ is weighted by $P(y\vert x)$ with $\lambda(y)$, for all $y\in Y$.

➁similarly, for node $W$,
$\lambda(w)$
=$P(e_{W}^{-}\vert w)$
=$P(e_{WX}^{-}\vert w)$
=$\sum_{x}P(x\vert w)\cdot\lambda(x)$
$\Rightarrow\lambda(W)$=$P(X\vert W)\cdot\lambda(X)$

Propagation Illustration In Multiple Child Nodes

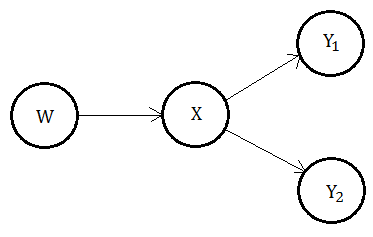
Now take a look at the illustration for the case of multiple child nodes.

[1] Backward propagation

This time, we begin by inspecting the behavior in $\lambda$. We have evidence on the subtree at node $X$ partitioned into 2 disjoint sets $e_{XY_{1}}^{-}$,$e_{XY_{2}}^{-}$.
➀as $X$ receives backward propagated evidence from $Y_{1}$, $Y_{2}$, the backward propagation is in joint distribution form:
$\lambda(x)$…$x\in X$
=$P(e_{X}^{-}\vert x)$
=$P(e_{XY_{1}}^{-}\vert x)\cdot P(e_{XY_{2}}^{-}\vert x)$
=$\prod_{Y_{i}\in Y}P(e_{XY_{i}}^{-}\vert x)$…multiple $Y_{i}$ children
$\Rightarrow\lambda(x)$=$\lambda_{Y_{1}}(x)\cdot\lambda_{Y_{2}}(x)$
➁as $X$ backward propagates the evidence to $W$:
$\lambda(w)$…$w\in W$
=$\sum_{x}P(x\vert w)\cdot\lambda(x)$
$\Rightarrow\lambda_{X}(W)$=$P(X\vert W)\cdot\lambda(X)$

[2] Forwardward propagation

➀as to the forward propagated evidence in node $X$, that’s $\pi(X)$, we evaluate it from its parent node $W$.
$\pi(x)$…$x\in X$
=$P(x\vert e_{X}^{+})$
=$P(x\vert e_{WX}^{+})$
=$\sum_{w}P(x\vert w)\cdot\pi(w)$
$\Rightarrow\pi(X)$=$P(X\vert W)\cdot\pi(W)$

[3] Forwardward propagation to multiple descendent

The forward propagated evidence in node $X$ would be taken into 2 distinct parts. Consider the evidence forward propagated from $X$ to $Y_{1}$, it consists of 2 major factors:
➀the forward propagated evidence from $W$.
➁the backward propagated evidence from $Y_{2}$.
The point is that the total forward propoagated evidence from $X$ to $Y_{2}$ is the joint probability function in combinatory format of these 2 factors.
$\pi_{Y_{1}}(x)$
=$P(x\vert e_{X}^{+},e_{Y_{2}}^{-})$
=$\frac {P(e_{Y_{2}}^{-}\vert x,e_{X}^{+})\cdot P(x\vert e_{X}^{+})}{P(e_{Y_{2}}^{-}\vert e_{X}^{+})}$
=$\frac {P(e_{Y_{2}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})}{P(e_{Y_{2}}^{-}\vert e_{X}^{+})}$
, where $x\in X$ and $e_{Y_{2}}^{-}\in e_{X}^{-}$, more precisely, we can take $e_{Y_{2}}^{-}$=$e_{XY_ {2}}^{-}$, next to expand it.

[4] Forwardward propagation to multiple descendent: extension proof::mjtsai1974

Continue from $\pi_{Y_{1}}(x)$:
➀multiply nominator and denominator by $P(e_{Y_{1}}^{-}\vert x)$:
$\pi_{Y_{1}}(x)$
=$\frac {P(e_{Y_{2}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})\cdot P(e_{Y_{1}}^{-}\vert x)}{P(e_{Y_{2}}^{-}\vert e_{X}^{+})\cdot P(e_{Y_{1}}^{-}\vert x)}$
➁$P(e_{Y_{2}}^{-}\vert e_{X}^{+})$
=$\sum_{x}P(e_{Y_{2}}^{-}\vert x,e_{X}^{+})\cdot P(x\vert e_{X}^{+})$
=$\sum_{x}P(e_{Y_{2}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})$
=$\alpha_{XY_{2}}^{-1}$
=$P(e_{XY_{2}}^{-})$…$e_{Y_{2}}^{-}$ and $e_{X}^{+}$ are independent
➂we also have further deduction below for $P(e_{X}^{-})$:
$P(e_{Y_{2}}^{-}\vert e_{X}^{+})\cdot P(e_{Y_{1}}^{-}\vert x)$
=$\sum_{x}P(e_{Y_{2}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})\cdot P(e_{Y_{1}}^{-}\vert x)$
=$P(e_{X}^{-})$
=$\alpha_{X}^{-1}$
➃therefore, rewrite ➀:
$\pi_{Y_{1}}(x)$
=$P(x\vert e_{X}^{+},e_{Y_{2}}^{-})$
=$\frac {P(e_{Y_{2}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})\cdot P(e_{Y_{1}}^{-}\vert x)}{P(e_{XY_{2}}^{-})\cdot P(e_{Y_{1}}^{-}\vert x)}$
=$\frac {P(e_{Y_{2}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})\cdot P(e_{Y_{1}}^{-}\vert x)}{\alpha_{XY_{2}}^{-1}\cdot P(e_{Y_{1}}^{-}\vert x)}$
=$\frac {\alpha_{XY_{2}}\cdot P(e_{Y_{2}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})\cdot P(e_{Y_{1}}^{-}\vert x)}{P(e_{Y_{1}}^{-}\vert x)}$
=$\frac {Bel_{Y_{1}}(x)}{\lambda_{Y_{1}}(x)}$
Here, we take $Bel_{Y_{1}}(x)$
=$\alpha_{XY_{2}}\cdot P(e_{Y_{2}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})\cdot P(e_{Y_{1}}^{-}\vert x)$

[5] Forwardward propagation to multiple descendent: generalization

Given that node $X$ has $n$ multiple child nodes $\{Y_{1},…,Y_{n}\}$, then, the forward propagated evidence from $X$ to $Y_{k}$ could be generalized in below expression:
$\pi_{Y_{k}}(x)$
=$\frac {Bel_{Y_{k}}(x)}{\lambda_{Y_{k}}(x)}$
, where $Bel_{Y_{k}}(x)$=$\alpha_{XY_{k}}\cdot\prod_{i\neq k} P(e_{Y_{i}}^{-}\vert x)\cdot P(x\vert e_{X}^{+})$

Propagation Illustration In Multiple Parent Nodes

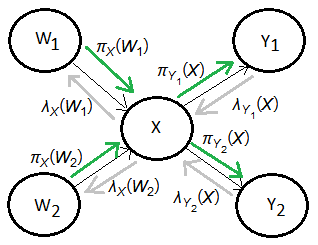
Causal polytree is the structure to be used in this section, each node might have multiple parents.

[1] Forward propagation

➀the predictive support at $X$ comes from its 2 parents $W_{1}$, $W_{2}$.
$\pi(x)$…$x\in X$
=$P(x\vert e_{X}^{+})$
=$P(x\vert e_{W_{1}X}^{+},e_{W_{2}X}^{+})\cdot P(x\vert W_{1},W_{2})$
=$P(x\vert e_{W_{1}X}^{+})\cdot P(x\vert e_{W_{2}X}^{+})\cdot P(x\vert W_{1},W_{2})$
=$\sum_{w_{1}}\sum_{w_{2}}P(x\vert e_{W_{1}X}^{+})\cdot P(x\vert e_{W_{2}X}^{+})\cdot P(x\vert w_{1},w_{2})$
=$\sum_{w_{1}}\sum_{w_{2}}\pi_{W_{1}}(x)\cdot\pi_{W_{2}}(x)\cdot P(x\vert w_{1},w_{2})$
➁the generalization of forward propagation at $X$ for $n$ parents:
$\pi(x)$=$\sum_{w_{1},…,w_{n}}\pi_{W_{1}}(x)\cdots\pi_{W_{n}}(x)\cdot P(x\vert w_{1},…,w_{n})$
➂as the forward propagation from $X$ to one of its child, say $Y_{k}$, it will have to combine the forward propagation thus obtain above with the backward propagated evidence from $\{Y_{1},…,Y_{k-1},Y_{k+1},…,,Y_{m}\}$, suppose $X$ has $m$ multiple child nodes.

[2] Backward propagation

➀the diagnostic support at $X$ comes from its 2 children $Y_{1}$, $Y_{2}$, where $\lambda(x)$=$\lambda_{Y_{1}}(x)\cdot\lambda_{Y_{2}}(x)$, must be splitted into 2 parts to be transfered to $W_{1}$, $W_{2}$, which are $\lambda_{X}(w_{1})$,$\lambda_{X}(w_{2})$.
➁to diagnose in $W_{1}$ the symptom/evidence backward propagated from $X$:
$\lambda_{X}(w_{1})$
=$P(e_{W_{1}X}^{-}\vert W_{1})$
=$P(e_{X}^{-},e_{W_{2}X}^{+}\vert W_{1})$
=$P(e_{X}^{-}\vert W_{1})\cdot P(e_{W_{2}X}^{+}\vert W_{1})$
=$P(e_{X}^{-}\vert x)\cdot P(x\vert W_{1})\cdot P(e_{W_{2}X}^{+})$
=$P(e_{X}^{-}\vert x)\cdot P(x\vert W_{1},W_{2})\cdot S_{1}\cdot P(e_{W_{2}X}^{+})$
=$P(e_{X}^{-}\vert x)\cdot P(x\vert W_{1},W_{2})\cdot S_{2}\cdot P(W_{2}\vert e_{W_{2}X}^{+})$
=$P(e_{X}^{-}\vert x)\cdot P(x\vert W_{1},W_{2})\cdot\beta\cdot P(e_{W_{2}X}^{+}\vert W_{2})$
=$\beta\sum_{x}\lambda(x)\cdot\sum_{w_{2}}P(x\vert w_{1},w_{2})\cdot\pi_{W_{2}}(x)$
, where the $S_{1}$,$S_{2}$,$\beta$ are arbitrary constants to hold the equality. We turn from $P(W_{2}\vert e_{W_{2}X}^{+})$ to $P(e_{W_{2}X}^{+}\vert W_{2})$ to express the deduction in terms of $\pi_{W_{2}}(x)$ for its simplicity.
➂the generalization of $n$ multiple parents:
$\lambda_{X}(w_{i})$
=$\beta\sum_{x}\lambda(x)$
$\;\;\cdot\sum_{w_{k}:k\neq i}P(x\vert w_{1},…,w_{n})$
$\;\;\cdot\prod_{k=1:k\neq i}^{n}\pi_{W_{k}}(x)$

[Cautions]

The belief updated by propagation would result in expensive computation consumption when there exists multiple parents. The introduction of propagation aims to eliminate the potential expensive computation of NP-hard order in variable elimination, now it seems that it is struggling over. Next to see the clique tree series, to be believed workable in a lot references.

Addendum

➀A T utorial on Bayesian Belief Networks, Mark L Krieg, Surveillance Systems Division Electronics and Surveillance Research Laboratory, DSTO-TN-0403
➁Lecture 4: Probability Propagation in Singly Connected Bayesian Networks, Duncan Fyfe Gillies, Department of Computing Imperial College London