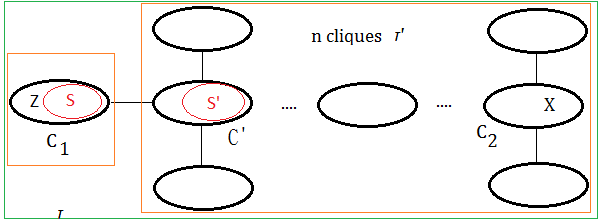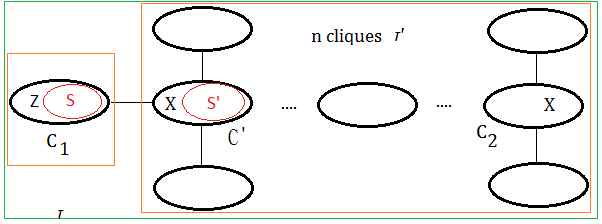The Clique Tree Construction

14 Oct 2018

Prologue To The Clique Tree Construction

The construction of clique tree aims at minimal cliques with none of them being the subsets of their neighbors, by using VE(variable elimination) in moral graph.

VE Versus Clique Tree Propagation

In my early post Variable Elimination Order And Moral Graph, we have explored how to query non-directly connected variables in the BN by means of VE and have a clear mapping in the MN. In advance to construct the clique tree, recap the VE and make comparison with clique tree propagation.

[1] Variable elimination

➀answers one query at a time, for query of other variables, the whole VE must be proceeded.
➁delete non-queried variables during VE process.
➂no computation sharing among different queries.

[2] Clique tree propagation

➀make posterior belief update for all variables, inclusive of these un-observed variables.
➁delete no any variable in the propagation of message passing.
➂allows computation sharing among different queries.

Since clique tree propagation could be distributed on un-observed variables, empirical results suggest to use it when we’d like to make posteriro belief update on un-observed variables.

Clique Tree Construction Algorithm

[1] Target

Given a BN, the target would be:
➀construct a clique tree that covers the BN, with its clique be the smallest.
➁by using VE in the moral graph as the solution.

[2] Algorithm

There exists over a dozen of clique tree construction algorithm, I list one workable and rather simple workflow, from Introduction to Bayesian Networks, Lecture 5: Inference as Message Propagation, Nevin L. Zhang, lzhang@cse.ust.hk, Department of Computer Science and Engineering, Hong Kong University of Science and Technology, Fall 2008, all related illustration in this article are under progress of this algorithm.
In the incoming future, I might have my own version of algorithm.

[3] Illustration by example

Given the same BN, suppose the elimination order is $X,A,S,D,B,L,T,R$, proceed with the following steps:
➀moralize the BN to get the MN. ➁eliminate variable $X$, we get the clique $(X,R)$:
➂eliminate variable $A$, we get the clique $(A,T)$:
➃eliminate variable $S$, we get the clique $(L,S,B)$, where the green line is the new pairwise connection after $S$ has been removed:
➄eliminate variable $D$, we get the clique $(R,D,B)$:
➅eliminate variable $B$, we get the clique $(L,R,B)$:
➆eliminate variable $L$, we get the final clique $(T,L,R)$:
Finally, connect the cliques thus obtained in accordance to the moralized MN.

[4] The clique tree is not unique

➀will the different elimination order construct clique tree identical to the moralized MN, or the original BN?
➁the clique tree is not unique, if we are using different elimination orders.

Due to above concern, will the posterior belief update all the same in the clique tree thus constructed, versus VE? I will prove my answer in the following sections.

Slight Different Elimination Order Constructed Clique Tree Makes The Same Propagation::by mjtsai1974

In this section, I’d like to prove that constructing clique tree by using slight different elimination order would just make the same propagation.

[Question]

Suppose we are give the same above BN, this time, the elimination order is $X,A,S,B,D,L,T,R$, with the clique tree thus constructed, we are asked for the same $P(L\vert X=y,A=y)$, what’s it?

[1] Clique tree construction

Suppose we are give the same above BN, with $X,A,S,B,D,L,T,R$ as the elimination order, proceed with the following steps:
➀moralize the BN to get the MN.
➁eliminate variable $X$, we get the clique $(X,R)$.
➂eliminate variable $A$, we get the clique $(A,T)$.
➃eliminate variable $S$, we get the clique $(L,S,B)$, where the green line is the new pairwise connection after $S$ has been removed:
➄eliminate variable $B$, we get the clique $(R,L,D,B)$, where the green line is the new pairwise connection after $B$ has been removed:
➅eliminate variable $D$, we get the clique $(R,L,D)$:
➆eliminate variable $L$, we get the final clique $(T,L,R)$:
Finally, connect the cliques thus obtained in accordance to the moralized MN(This might not be a perfect clique tree).

[2] What is $P(L\vert X=y,A=y)$?

Choose $(R,L,D)$ as the pivot:
➀$f_{1}$ and $f_{2}$ are the same:
$f_{1}(T)$=$P(A=y)\cdot P(T\vert A=y)$
$f_{2}(R)$=$P(X=y\vert R)$
➁$f_{3}(L,R)$=$\sum_{T}P(R\vert T,L)\cdot f_{1}(T)\cdot f_{2}(R)$
➂$f_{4}(L,B)$=$\sum_{S}P(S)\cdot P(L\vert S)\cdot P(B\vert S)$
➃$f_{5}(R,D)$=$\sum_{B}P(D\vert R,B)$
➄take $H_{\alpha}(R,L,D)$
=$\sum_{B}f_{3}(L,R)\cdot f_{4}(L,B)\cdot f_{5}(R,D)\cdot 1$ as the joint probability function in this clique tree.
➅compare with the $H(R,L,B)$ in The Bayesian Network Propagation And Clique Tree, we turn $f_{5}(R,D)$ into $f_{5.5}(R,B)$:
$f_{5.5}(R,B)$=$\sum_{D}P(D\vert R,B)$, therefore,
$H_{\alpha}(R,L,D)$
=$\sum_{B}f_{3}(L,R)\cdot f_{4}(L,B)\cdot f_{5}(R,D)\cdot 1$
=$f_{3}(L,R)\cdot f_{4}(L,B)\cdot f_{5.5}(R,B)\cdot 1$
=$H_{\alpha}(R,L,B)$ in this clique tree.
=$H(R,L,B)$ in The Bayesian Network Propagation And Clique Tree

The answer of $P(L\vert X=y,A=y)$ would just be the same!!!

The clique trees are compared in below graph, the new tree is under the original tree:
The functions associated with original clique tree are listed below:
$f_{1}(T)$=$P(A=y)\cdot P(T\vert A=y)$
$f_{2}(R)$=$P(X=y\vert R)$
$f_{3}(L,B)$=$\sum_{S}P(S)\cdot P(L\vert S)\cdot P(B\vert S)$
$f_{4}(R,B)$=$\sum_{D}P(D\vert R,B)$
$f_{5}(L,R)$=$\sum_{T}f_{1}(T)\cdot f_{2}(R)\cdot P(R\vert T,L)$
$H(R,L,B)$=$f_{3}(L,B)\cdot f_{4}(R,B)\cdot f_{5}(L,R)\cdot 1$

Very Different Elimination Order Constructed Clique Tree Makes The Same Propagation::by mjtsai1974

In this section, I’d like to prove that by using very different elimination order in clique tree construction process will you get the identical propagation of message passing for the same given BN.

[Question]

Suppose we are give the same above BN, this time, the elimination order is $X,A,T,R,B,D,L,S$, with the clique tree thus constructed, we are asked for the same $P(L\vert X=y,A=y)$, what’s it?

[1] Clique tree construction

Assume we are give the same above BN, the elimination order is $X,A,T,R,B,D,L,S$, proceed with the following steps: ➀moralize the BN to get the MN.
➁eliminate variable $X$, we get the clique $(X,R)$.
➂eliminate variable $A$, we get the clique $(A,T)$.
➃eliminate variable $T$, we get the clique $(T,L,R)$.
➄eliminate variable $R$, we get the clique $(R,L,D,B)$.
➅eliminate variable $B$, we get the clique $(B,S,D)$.
➆eliminate variable $D$, we get the clique $(L,S,D)$.
Finally, connect the cliques thus obtained in accordance to the moralized MN(This might not be a perfect clique tree).

[2] What is $P(L\vert X=y,A=y)$?

Choose $(T,L,R)$ as the pivot:
➀$f_{1}$ and $f_{2}$ are the same:
$f_{1}(T)$=$P(A=y)\cdot P(T\vert A=y)$
$f_{2}(R)$=$P(X=y\vert R)$
➁$f_{3}(L,D)$=$\sum_{S}P(L\vert S)\cdot P(S)$
➂$f_{4}(B,D)$=$\sum_{S}P(B\vert S)\cdot P(S)$
➃$f_{5}(R)$=$\sum_{B,D}P(D\vert R,B)\cdot f_{3}(L,D)\cdot f_{4}(B,D)$
➄take $H_{\beta}(T,L,R)$
=$P(R\vert T,L)\cdot f_{1}(T)$
$\;\;\cdot f_{2}(R)\cdot f_{5}(R)$ as the joint probability function in this clique tree.
➅compare with the $H(R,L,B)$ in The Bayesian Network Propagation And Clique Tree, we turn $f_{5}(R)$ into $f_{5.5}(R,B)$:
$f_{5.5}(R,B)$=$\sum_{D}P(D\vert R,B)\cdot f_{3}(L,D)\cdot f_{4}(B,D)$, therefore,
$H_{\beta}(T,L,R)$
=$P(R\vert T,L)\cdot f_{1}(T)$
$\;\;\cdot f_{2}(R)\cdot f_{5}(R)$
=$\sum_{T}P(R\vert T,L)\cdot f_{1}(T)$
$\;\;\cdot f_{2}(R)\cdot f_{5.5}(R,B)$
=$H_{\beta}(R,L,B)$
=$H(R,L,B)$ in The Bayesian Network Propagation And Clique Tree

The answer of $P(L\vert X=y,A=y)$ would just be the same!!!

The clique trees are compared in below graph, the new tree is under the original tree:
The functions associated with original clique tree could be found in prior section.

The Target: Minimal Clique Trees

A clique tree is minimal if none of its cliques are subsets of their neighbors, the ideal version after variable elimination should be minimal.
Below exhibits different VE leads to different clique trees(non-minimal):
The ideal minimal clique tree would the illustration:
Current introduced buildCliqueTree() algorithm might not guarantee to have the minimal result, in the incoming future, I might develop a new algorithm for this. (to be conti…)

Clique Tree Is Variable-Connected

The clique tree by buildCliqueTree() from the un-connected MN is variable-connected.

proof::mjtsai1974

By using mathematics induction fashion, we can prove it.

[1] the case of $1$ clique

Suppose only one clique in the tree, this just holds.

[2] the case of $n$ cliques

Suppose it holds for $n$ cliques in the tree $\tau’$, next to prove it holds for $n+1$ cliques in the tree $\tau$. Below is the pre-requisite to next prove step:
➀the tree $\tau’$ contains cliques $C_{1}$ and $C_{2}$ with variable $X$ in it.
➁since $\tau’$ is the clique tree, variable $X$ exists in all the cliques of the path in between $C_{1}$ and $C_{2}$.

[3] the case of $n+1$ cliques

We’d like to show $X$ exists in all the cliques of the path in between $C_{1}$ and $C_{2}$ in tree of $n+1$ cliques.
To create tree $\tau$, we make below assumption:
➀$C_{1}$ is the clique by removing variable $Z$, where variable $X$ is not $Z$(since $X\in C_{1}\cap C_{2}$), therefore $X\in S$.
➁$\tau’$ is the tree obtained after ➀.
➂suppose $S’$ is obtained by removing some other node in $S$(not $X$), then $S’ \subseteq S$.
➃or suppose $S’$ is obtained by removing some other variables in adjacent to all variables in $S$, then $S’$=$S$.
➄for bothe case $S’ \subseteq S$ or $S’$=$S$, then $X\in S$ and $X\in S’$ must all hold. By taking $\tau$=$C_{1}$+$\tau’$, trivially, the variable exists in the cliques of the path in between $C_{1}$ and $C_{2}$.

Evenmore, for the condition that keeping ➀,➁ the same, where $S’$ is obtained by removing variable $X$ from $S$, then $S’ \subset S$, that is to say $C’$=$S’\cup X$. By taking $\tau$=$C_{1}$+$\tau’$, we also find it true that the variable exists in the cliques of the path in between $C_{1}$ and $C_{2}$.

Addendum

➀Introduction to Bayesian Networks, Lecture 5: Inference as Message Propagation, Nevin L. Zhang, lzhang@cse.ust.hk, Department of Computer Science and Engineering, Hong Kong University of Science and Technology, Fall 2008
➁Clique Tree Algorithm - Computation
➂Clique Trees, Amr Ahmed, CS CMU, October 23, 2008
➃Graphical Models - Lecture 11: Clique Trees, Andrew McCallum, mccallum@cs.umass.edu