Temporal Difference Learning - Part 2
22 Jan 2019Prologue To The Temporal Difference Learning - Part 2
$TD(0)$ Algorithm: $\lambda$=$0$
This is by taking $\lambda$=$0$ in $TD(\lambda)$ algorithm.
[The rule]Eposide $T$:
[Notes]
$\;\;$For all $S$, $e(S)$=$0$ at start of eposide, $V_{T}(S)$=$V_{T-1}(S)$
$\;\;$After $S_{t-1}\xrightarrow{r_{t}}S_{t}$:(from step $t-1$ to $t$ with reward $r_{t}$)
$\;\;\;e(S_{t-1})$=$e(S_{t-1})$+$1$:
$\;\;\;\;$Update eligibility of $S_{t-1}$ after arriving to $S_{t}$
$\;\;$For all $S$,
$\;\;V_{T}(S)$=$V_{T-1}(S)$+$\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1}))$…[A]
$\;\;\;e(S_{t-1})$=$0\cdot\gamma\cdot e(S_{t-1})$=$0$:
$\;\;\;\;$before transite from $S_{t-1}$ to $S_{t}$ in next iteration, we can easily tell that the eligibility of state $S$ is always zero.➀the 2nd part of (A) is sum of the reward plus the the discounted value of the state we just arrived, minus the state value we just left; where these state values are all evaluated in last iteration. It could just be the temporal difference.
[Caution]
➁we are going to apply the temporal difference onto $S$ itself only, with no proportion to the eligibility of any other states, and the learning rate would be specified for we don’t want it to move too much.
➂after the state has been iterated, decay or decrease its eligibility with $\lambda\cdot\gamma$, in their given value, in $TD(0)$, $\lambda$=$0$, the eligibility of state $S$ is always zero.
➃and we are backing up to next stae.➀all the $S$ are all being done in similar approach.
➁the value at state $S$(the $S$ in [A]) is going to be updated on this quantity, $r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1})$, which is the same for everybody, doesn't depend on which $S$ we are updating, and $e(S)$=$1$ is specific to the state $S$ at the moment we are evaluating(looking at).
MLE(Maximum Likelihood Estimate) And $TD(0)$ Algorithm
[1] MLEGiven data of a lot trajectories and we are under the condition that we are in $S_{t-1}$, and we don’t know what state we are going to end up in. But, there exists some probability of $r_{t}$+$\gamma\cdot V_{T-1}(S_{t})$-$V_{T-1}(S_{t-1})$.
If we take expectation of [A], then:
$V_{T}(S_{t-1})$=$E_{S_{t}}[r_{t}+\gamma\cdot V_{T-1}(S_{t})]$…[B]
We could treat it as the MLE of $V_{T}(S_{t-1})$ over all possible $V_{T-1}(S_{t})$. What we are doing is just sampling different possible $S_{t}$ values, that is $V_{T-1}(S_{t})$, and is crossing over different trajectories for we have dataset of trajectories.We are just taking an expectation over what we get as the next state of the reward plus the discounted estimated value(evaluated in last eposide) of that next state.
[2] Why [B] is supposed to be the MLE?$\;\;$[B] is the MLE
proof::mjtsai1974➀$V_{T}(S_{t-1})$
=$V_{T-1}(S_{t-1})$+$\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1}))$
=$V_{T-1}(S_{t-1})\cdot(1-\alpha_{T})$+$\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t}))$…[B.1]
This is the value of $S_{t-1}$ in eposide $T$, when transiting from $S_{t-1}$ to $S_{t}$, and remind that we are given data of a lot trajectories with each containing state transition in it.
➁suppose we are in $S_{t-1}$ in one trajectory, and the next $S_{t}$ does exist, there exists $k$ such $S_{t}$ and $n-k$ different states of $S_{t}$, and totally $n$ trajectories in the given data. Therefore, there exists some probability $P(S_{t}\vert S_{t-1})$=$\frac {k}{n}$.
➂$V_{T}(S_{t-1})$
=$\sum_{S{t}}P(S_{t}\vert S_{t-1})\cdot([B.1])$
=$E_{S_{t}}[r_{t}+\gamma\cdot V_{T-1}(S_{t})]$ just holds.
, where $V_{T-1}(S_{t-1})\cdot(1-\alpha_{T})$ and $\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t}))$ are some values varying in each trajectory, the former is the departuring state, the later is the ending state, $\alpha_{T}$ is the learning rate, depends on how you would like the learning process to be. I just use the term $r_{t}+\gamma\cdot V_{T-1}(S_{t})$ to be the random variable to be taken expectation.
Illustration: The Idea Of TD(0) After TD(1)
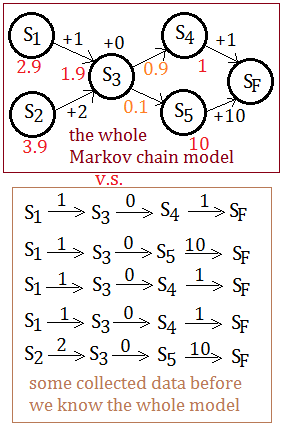
[1] The given exampleSucceeding to the same example as part 1 article, this time we are given data of 5 trajectories, the red quantity is the value of the state after backup propagation with $\gamma$=$1$. Recall that each distinct state’s initial value is $0$. We’d like to ask for the value of $S_{2}$ in the 5-th eposide.
[2] By using TD(1)
➀we can deduce it out the temporal difference term:
[3] By using MLE
$\triangle V_{T}(S_{2})$
=$r_{2}$+$\gamma\cdot r_{3}$+$\gamma^{2}\cdot r_{5}$+$\gamma^{3}\cdot V_{T-1}(S_{F})-V_{T-1}(S_{2})$
=$12$
➁$V_{T}(S_{2})$
=$V_{T-1}(S_{2})$+$\triangle V_{T}(S_{2})$
=$0$+$12$
=$12$$V_{T}(S_{2})$
=$r_{2}$+$\gamma\cdot P(S_{3}\vert S_{2})\cdot V_{T}(S_{3})$
=$r_{2}$+$\gamma\cdot P(S_{3}\vert S_{2})\cdot [r_{3}$
$\;\;$+$\gamma\cdot (P(S_{4}\vert S_{3})\cdot(V_{T}(S_{4}))$
$\;\;\;\;$+$P(S_{5}\vert S_{3})\cdot (V_{T}(S_{5}))]$
=$r_{2}$+$\gamma\cdot P(S_{3}\vert S_{2})\cdot [r_{3}$
$\;\;$+$\gamma\cdot (P(S_{4}\vert S_{3})\cdot(r_{4}+\gamma\cdot P(S_{F}\vert S_{4})\cdot V_{T}(S_{F}))$
$\;\;\;\;$+$P(S_{5}\vert S_{3})\cdot (r_{5}+\gamma\cdot P(S_{F}\vert S_{5})\cdot V_{T}(S_{F})))]$, and from data, we have probability of transition that
➀$\gamma$=$1$
➁$P(S_{3}\vert S_{2})$=$1$
➂$P(S_{4}\vert S_{3})$=$0.6$
➃$P(S_{5}\vert S_{3})$=$0.4$
➄$P(S_{F}\vert S_{4})$=$1$
➅$P(S_{F}\vert S_{5})$=$1$Therefore,
$V_{T}(S_{2})$
=$2$+$1\cdot 1\cdot [0$
$\;\;$+$1\cdot (0.6\cdot(1+1\cdot 1\cdot 0)$
$\;\;\;\;$+$0.4\cdot (10+1\cdot 1\cdot 0))]$
=$6.6$, by the same approach, $V_{T}(S_{1})$=$5.6$.Cautions must be made that by using MLE for $V_{T}(S_{2})$, we choose to refer to the same eposide $T$, not $T-1$, why?
[4] The breakdown
This is all due to we are doing the estimiation by using data.Please recall in Temporal Difference Learning - Part 1, I have figured out that $V_{T}(S_{1})$=$2.9$, $V_{T}(S_{2})$=$3.9$, $V_{T}(S_{3})$=$1.9$, by using both backup propagation and expect discounted reward in the section of ReCap The Backup In Markov Chain.
The MLE of $V_{T}(S_{2})$=$6.6$, which is more, whereas the $TD(1)$ estimate is $12$, a lot more, all wrong, except for $V_{T}(S_{2})$=$3.9$ by using backup based on the whole model. Why MLE is less wrong? Why $TD(1)$ estimate is so far off?
➀when we compute the $TD(1)$ estimate, we use only the 5-th trajectory, one of the five trajectories to propagate the information back.
➁when we use MLE for the estimation, we use all data, more information, more accurate. The more might not be the better, but, we can resort the inaccuracy of MLE of $V_{T}(S_{2})$=$6.6$ to that we don't have the complete data set to build this whole MC model.Specifically be noted that $TD(1)$ is alos be treated as outcome-based estimate for it uses the immedaite reward and ignores the intermediate encountered states' value.
[5] A tiny findingWe have a tiny finding that $TD(0)$ relates current state's value to next most closed state's value, is more like MLE estimate, even if we are using it in one trajectory, the 5-th in this illustration.
The temporal difference is about to learn to make prediction of states value for these states transit over time in the unit of one distinct trajectory, whereas the MLE tends to estimate states’ value accrossing all trajectories in given sample.
The argument in between $TD(0)$, $TD(1)$ and MLE is in that we don't have the full image of the Markov chain model, with only a little sampling data.
The Outcome Based v.s. The Intermediate Estimate Based::mjtsai1974
[1] Summary of these equationsI’d like to step further to deeper inside in the concept with $TD(0)$ and $TD(1)$. Given below 3 expression:
[2] Why toss out $\gamma^{k}\cdot V_{T-1}(S_{t+k})-V_{T-1}(S_{t-1})$?
➀$V_{T}(S_{t-1})$
=$V_{T-1}(S_{t-1})$+$\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1}))$…[A]
➁$V_{T}(S_{t-1})$
=$E_{S_{t}}[r_{t}+\gamma\cdot V_{T-1}(S_{t})]$…[B]
➂$V_{T}(S_{t-1})$
=$E[r_{t}+\gamma\cdot r_{t+1}+\gamma^{2}\cdot r_{t+2}+\gamma^{3}\cdot r_{t+3}+…]$…[C]
, where [A] is the regular expression in temporal difference, works for both $TD(0)$ and $TD(1)$, the difference is in $TD(0)$ rule the eligibility of the evaluated state would be reset to $0$; the equation [B] is by taking expect of [A], more description is in $TD(0)$ related section; whereas [C] is the idea by taking only the reward sequence that we saw, ignoring the estimate we might have gotten in some other states, which is the spiritual $TD(1)$.Moreover, the full [C] expression should be refined as:
$V_{T}(S_{t-1})$
=$E[r_{t}+\gamma\cdot r_{t+1}+\gamma^{2}\cdot r_{t+2}$
$\;\;+…+\gamma^{k-1}\cdot r_{t+k-1}+\gamma^{k}\cdot V_{T-1}(S_{t+k})-V_{T-1}(S_{t-1})]$…[D]The reason we ignore these 2 terms $\gamma^{k}\cdot V_{T-1}(S_{t+k})-V_{T-1}(S_{t-1})$ is that when $k$ is quiet large, the $\gamma^{k}$ would then approach $0$, and $V_{T-1}(S_{t-1})$'s initial value is $0$ in one eposide, if $S_{t-1}$ is the target state to be evaluated, especially the very first time it is evaluated.
[3] Evaluation on [B] and [C]By using [C], is just like the $S_{2}$ in the 5-th trajectory in above illustrated example, however, when the trajectory is an infinite series, the $TD(1)$ also does the right thing, repeating that update over and over again won't change anything, because the expectation is the expectation expressed in terms of the saw rewards.
By using [B], it takes the intermediate estimates that we have computed and refined on all the intermediate nodes, that is taking all the states we encountered along the way into concern to improve our estimate of the value of every other state.
Therefore, [B] is more self-consistent of connecting the value of states to the value of the other states you want(or encountered), and [C] is just using the experience that it saws and ignores the existence of the intermediate states.
[4] CautionsAll above are under the condition that we have been given partial, incomplete data before we know the full model of state transition, or even if we are given the complete data of a target model to be predicted, we still believe that we don’t have it yet!!
[5] The appropriate apply::mjtsai1974Trivially, [D] relates the final state value of $V_{T-1}(S_{t+k})$ to the target evaluated state $S_{t-1}$ in eposide $T$, whose value is expressed in terms of $V_{T-1}(S_{t-1})$.
$V_{T}(S_{t-1})$
=$E[r_{t}+\gamma\cdot r_{t+1}+\gamma^{2}\cdot r_{t+2}$
$\;\;+…+\gamma^{k-1}\cdot r_{t+k-1}+\gamma^{k}\cdot V_{T-1}(S_{t+k})-V_{T-1}(S_{t-1})]$The point is:
[6] After $k$ is large enough::mjtsai1974
➀how large $k$(the length of trajectory) should be for we to safely toss out these 2 terms?
➁before $k$ is large enough, we should be able to calculate(or incorporate) new arrivaed state's value, which is reasonable to relate current arrived state to the target evaluated state, repeat this behavior until $k$ is large enough.Evenmore, after $k$ is large enough to ignore these 2 terms, the algorithm should have a design to go back to re-calculate the target state’s value, the transition must range from $S_{t-1}$ to $S_{t+k-1}$, thus to move toward a bit more closed to have a much maturer condition to make a toggle of decision according to the new evaluated target state's value.
Finally, when $k$ is large enough, it means that we have state transition over a rather long horizon, we are safe to just use the experience of saw rewards, since the update term of intermediate nodes would just be cancel out by the temporal difference equation(like [A] with $\lambda\neq 0$), thought by mjtsai1974, and might be evaluated by program in the future(to be conti).