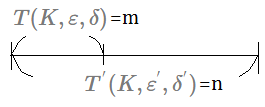Explore versus Exploit - Part 2

04 Sep 2019

Prologue To Explore versus Exploit - Part 2

Next would be to get the metrics to construct the fundamental basis of algorithm and validate the bandit arms strategy.

Metrics For Bandit Arm Selection

[1] Build some metrics

Still we are using the same bandit arms for illustration. To build an algorithm that can make the best bandit arm selection, always a or always b, we need to build some metrics:
➀Identify the optimal bandit arm in the limit.
➁maximize the discounted expected reward.
➂maximize the discounted expected reward over a finite horizon.
➃identify the $\varepsilon$ near optimal arm with high probability $1-\delta$ in the number of steps $T(K,\varepsilon,\delta)$, polynominal in $K$,$\frac {1}{\varepsilon}$,$\frac {1}{\delta}$…[A]
➄find the $\varepsilon$ nearly maximized reward with high probability $1-\delta$ in the number of steps $N(K,\varepsilon,\delta)$, polynominal in $K$,$\frac {1}{\varepsilon}$,$\frac {1}{\delta}$…[B]
➅pull an $\varepsilon$ non-near optimal or near sub-optimal bandit arm with high probability $1-\delta$ in no more than the number of steps $N^{'}(K,\varepsilon,\delta)$ times, polynominal in $K$,$\frac {1}{\varepsilon}$,$\frac {1}{\delta}$…[C]

Above metrics explicitly lead to the construction of reinforcement learning which is the fashion we’d like the algorithm to be executed with, where $K$ is he number of bandit arms.

[2] Identify the $\varepsilon$ near optimal arm...[A]

➀$\varepsilon$ near optimal doesn't mean that the arm we get is the absolute best arm.
➁we might be unlucky over a long long period and get a pull paid arm. It would be impossible to get the best arm within finite period of time.

For above constraints, what we want with [A] is to get a near optimal arm with only $\varepsilon$ distance from it, it might not workable all the time, but works with hight probability $1-\delta$.

The $T(K,\varepsilon,\delta)$ stands for the number of pulls before we get or have identified the near optimal arm, and it must be polynomial in $K$,$\frac {1}{\varepsilon}$,$\frac {1}{\delta}$.

Indeed, $T(K,\varepsilon,\delta)$ is a polynomial that bounds the number of steps/pulls before we get or have identified the near optimal arm.

[3] Find the $\varepsilon$ nearly maximized reward...[B]

It is a metric similar to [A], after [B] has been executed over the number of steps $N(K,\varepsilon,\delta)$, we can get the $\varepsilon$ nearly maximized reward.

$N(K,\varepsilon,\delta)$ is the the number of pulls/steps, for which I run that long with [B], I can get $\varepsilon$ nearly maximized reward, with high probability $1-\delta$.

Such number of steps $N(K,\varepsilon,\delta)$ must be polynomial in $K$,$\frac {1}{\varepsilon}$,$\frac {1}{\delta}$.

[B] puts more care on how we reach the optimal arm, not just we get the optimal arm. It focus more directly with rewards, for [A] might do a lot of unfortune trials with zero or a few pay off, we need to evaluate if current accumulated rewards is sufficient to be the incentive to keep going on in the same direction.

[4] Pull an $\varepsilon$ non-near optimal(naer sub-optimal) arm...[C]

This is a mistake bound. Inevitably, we might pull non-near optimal arm, the mistake arm.

We want to limit the number of pulls of such non-near optimal or sub-optimal arm to $N^{'}(K,\varepsilon,\delta)$, which is a small number.

It could be over a very very long time window, but the number of mistake pulls is really small, with high probability $1-\delta$.

[5] A brief summary - PAC

➀[A] focus more on identifying the best output, the near optimal arm, the exploitation.
➁[B] is the accumulated return of rewards, which is the exploration.
➂[C] is the mistake bound.

This looks like PAC(Probabily Approximately Correct) learning, some paper refer it PAO(Probabily Approximately Optimal). Even though above metrics are not fully correct, if the goal is to identify the best arm, we could regard it as classification.

The Equilibrium Of Metrics [A] And [B] And [C]

[1] The target of proof

The very next thing is to prove the transitivity in metrices [A],[B] and [C], that is to say:
$\;\;$Find Best$\Leftrightarrow$Low Mistakes$\Leftrightarrow$Doing Well

[2] Find Best$\Rightarrow$Low Mistakes

➀the beginning:
Given that you have an algorithm [A] that can identify $\varepsilon$ near optimal arm with high probability $1-\delta$ in the bounded number of pulls $T(K,\varepsilon,\delta)$, polynominal in $K$,$\frac {1}{\varepsilon}$,$\frac {1}{\delta}$.
➁next target:
We’d like to build another algorithm of low mistakes, the number of trials at which it pulls a non $\varepsilon'$ close(mistake) arm is bounded by $T^{'}(K,\varepsilon^{'},\delta^{'})$, where $\varepsilon'\geq\varepsilon$ and is high probability $1-\delta^{'}$.

proof:
$\Rightarrow$first by using algorithm [A], within bounded number of pulls $T(K,\varepsilon,\delta)$, we can find $\varepsilon$ near optimal arm with high probability $1-\delta$.

$\Rightarrow$then, what's the total number of mistakes [A] can make?
Since it is the bounded number of pulls, after that, we can find $\varepsilon$ near optimal arm, that is to say no more than $T(K,\varepsilon,\delta)$.

$T^{'}(K,\varepsilon^{'},\delta^{'})\leq T(K,\varepsilon,\delta)$
$\Rightarrow$why $T'(K,\varepsilon',\delta')$ is the total number of mistakes?
Because the idea of [A] is $\varepsilon$ near optimal arm, and the execution of [A] comes out the non $\varepsilon'$ close(or say $\varepsilon'$ near optimal) arm, where $\varepsilon'\geq\varepsilon$. And we treat the non $\varepsilon'$ close(or say $\varepsilon'$ near optimal) arm as the mistake arm.

$\Rightarrow$we thus prove find best[A]$\Rightarrow$low mistakes[C].

[3] Low Mistakes$\Rightarrow$Doing Well

➀the beginning:
Given that you have algorithm [C] that bounds the mistake pulls of $\varepsilon$ sub-optimal arms in $T(K,\varepsilon,\delta)$, with high probability $1-\delta$, polynominal in $K$,$\frac {1}{\varepsilon}$,$\frac {1}{\delta}$.
➁next target:
We’d like to build another algorithm that brings you the $\varepsilon'$ nearly maximized reward, in other words, $\varepsilon'$ close to optimal per step reward, with high probability $1-\delta’$, polynominal in $K$,$\frac {1}{\varepsilon’}$,$\frac {1}{\delta’}$.

proof:
$\Rightarrow$first by using algorithm [C], $T(K,\varepsilon,\delta)$ is the upper bound for mistake pulls, beyond this upper bound, you can do a lot pulls of correctness, say $T’(K,\varepsilon’,\delta’)$, take it as $n$, far more than this upper bound.

All the rest in $T’(K,\varepsilon’,\delta’)$ beyond $T(K,\varepsilon,\delta)$ have to be $\varepsilon’$ near optimal.

$\Rightarrow$here is one hint to remind you that from the point that you have pulled up to $T(K,\varepsilon,\delta)$ times, do you just start to make the pulls of right arm?

No, it's just [C] constraints the mistake pulls in $T(K,\varepsilon,\delta)$.

At this point, the distance from optimal reward would be greater than $\varepsilon$.

$\Rightarrow$this is a Bernoulli bandit, each pull gives you either zero or one paid. So, if you accumulate mistake pulls up to $T(K,\varepsilon,\delta)$ times, the total fail cases of mistake paid is $T(K,\varepsilon,\delta)\cdot 1$, we take it as $m$. At this moment, it is just $\varepsilon$ close to optimal, bypass the mistakes.

$\Rightarrow$the total sub-optimality over the end, left steps is $m+\varepsilon\cdot(n-m)$. And the average per step sub-optimality is $\frac {m+\varepsilon\cdot(n-m)}{n}$, where this average per step sub-optimality is greater than the distance to the optimal reward, that is to say $\varepsilon’\leq\frac {m+\varepsilon\cdot(n-m)}{n}$. Ideally, we want the distance $\varepsilon'$ optimal is smaller than the distance to the pull of mistake arms.

$\Rightarrow$if we take $\varepsilon$=$\frac {\varepsilon’}{2}$ to try to further narrow down the mistake pulls, above inequality becomes:
$\varepsilon’\geq\frac {m+\frac {\varepsilon’}{2}\cdot(n-m)}{n}$, then

$n\geq m\cdot(\frac {2}{\varepsilon'}-1)$

It is just the quantity that $n$ should have been to make algorithm [B] validate or concrete. We thus prove low mistakes[C]$\Rightarrow$doing well[B].

[4] Doing Well$\Rightarrow$Find Best

➀the beginning:
Given that you have algorithm [B] that can find the $\varepsilon$ nearly maximized reward, with high probability $1-\delta$, after it has been executed over the number of steps $T(K,\varepsilon,\delta)$, which is polynominal in $K$,$\frac {1}{\varepsilon}$,$\frac {1}{\delta}$.
➁next target:
We want to build an algorithm that can identify $\varepsilon’$ close to optimal arm, with high probability $1-\delta’$, after it has been pulled over $T’(K,\varepsilon’,\delta’)$ times.

proof:
$\Rightarrow$first by using algorithm [B], we do get the $\varepsilon$ nearly maximized reward arm, that’s the per step $\varepsilon$ nearly optimal reward arm.

If we keep following the probability distribution of this pull, I will get the same per step average.

$\Rightarrow$next to introduce $e_{i}$, the sub-optimality for the error of $arm_{i}$, that is you should have selected $arm_{i}$, and you havn’t during the execution of algorithm [C].

Such arm is chosen at least $\frac {1}{K}$ of the time, ideally, we want the error of sub-optimality is as small as possible, so the per step optimality $\varepsilon$ should be greater than or equal to $\frac {1}{K}\cdot e_{i}$, that is $\varepsilon\geq\frac {1}{K}\cdot e_{i}$.

$\Rightarrow$we also want this error of sub-optimality to be smaller than $\varepsilon’$, the distance to the most optimal arm, $\varepsilon’\geq e_{i}$, which is the constraint.
$\varepsilon\geq\frac {1}{K}\cdot e_{i}$…➀
$\varepsilon’\geq e_{i}$…➁

We relate $\varepsilon’$ to $\varepsilon$ by taking $\frac {\varepsilon’}{K}$=$\varepsilon$ in ➀, then ➁ holds, everything just holds.

$\Rightarrow$we just prove doing well[B]$\Rightarrow$find best[A], from the point we are $\varepsilon$ close to optimal reawrd, we can identify $\varepsilon'$ close to most optimal arm, where $\varepsilon'\leq\varepsilon$.

Put It Together

Here we can tell that
➀algorithm [A] is for exploitation, to get better estimate of optimal arm.
➁algorithm [B] is for exploration, to have better rewards.
➂algorithm [C] is a mistake bound.

Put it all together, we know that we need exploration and exploitation interchangeable.

Addendum

➀Exploring Exploration, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)