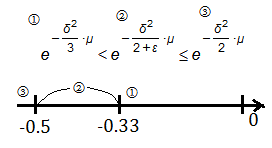Chernoff Bounds For Bernoulli Random Variable

09 Dec 2019

Prologue To The Chernoff Bounds For Bernoulli Random Variable

The Chernoff bounds is a technique to build the exponential decreasing bounds on tail probabilities. This article develops the tail bound on the Bernoulli random variable with outcome 0 or 1.

The Error Probability After Test

Let $X_{i}$ to be a Bernoulli random variable for $i$=$\{1,2,…,n\}$
➀$X_{i}$=$1$ with probability $p_{i}$
➁$X_{i}$=$0$ with probability $1$-$p_{i}$
, where all $X_{i}$s are I.I.D and suppose at least one of the $p_{i}$ is non-zero.

We are testing with a hope that we can make our target value meet the expectation level after some amount of trials. To express the target value we want in terms of expect value, we let $X$=$\sum_{i=1}^{n}X_{i}$, $E\lbrack X\rbrack$=$\mu$=$\sum_{i=1}^{n}p_{i}$.

[Question]

How confident we are in the final outcome by the random variable $X$? It is asking you 2 kinds of questions:
➀the range of the confidence interval
➁the error probability for the target value $X$ above or below the expect value $\mu$

The follwing section would guide you through the process to build the upper and lower bound of such error probability in Chernoff exponential decreasing form.

[Notes] Even if our proof of ➁ holds, the range of confidence interval must be guaranteed by the native design in your experiment.

The Upper Bound On Error Probability

It is asking the error probability when target value $X$ is greater than the expect value $\mu$, and we’d like to bound it on the upper side.

$P(X>(1+\delta)\cdot\mu)$, for $\delta>0$
=$P(e^{t\cdot X}>e^{t\cdot (1+\delta)\cdot\mu})$, for all $t>0$
$\leq \frac{E\lbrack e^{t\cdot X}\rbrack}{e^{t\cdot (1+\delta)\cdot\mu}}$…Markov inequality

Since each $X_{i}$ is independent, we have
$E\lbrack e^{t\cdot X}\rbrack$
=$E\lbrack e^{t\cdot \sum_{i=1}^{n}X_{i}}\rbrack$
=$E\lbrack e^{t\cdot (X_{1}+X_{2}+…+X_{n})}\rbrack$
=$E\lbrack \prod_{i=1}^{n} e^{t\cdot X_{i}}\rbrack$
=$\prod_{i=1}^{n} E\lbrack e^{t\cdot X_{i}}\rbrack$
=$\prod_{i=1}^{n} e^{t\cdot 1}\cdot p_{i}+e^{t\cdot 0}\cdot (1-p_{i})$
=$\prod_{i=1}^{n} e^{t}\cdot p_{i}+1\cdot (1-p_{i})$
=$\prod_{i=1}^{n} 1+(e^{t}-1)\cdot p_{i}$

Because $1+X<e^{X}$ for all $X>0$, we have
$E\lbrack e^{t\cdot X}\rbrack$
=$\prod_{i=1}^{n} 1+(e^{t}-1)\cdot p_{i}$
$<\prod_{i=1}^{n} e^{(e^{t}-1)\cdot p_{i}}$
=$e^{(e^{t}-1)\cdot (p_{1}+…+p_{n})}$
=$e^{(e^{t}-1)\cdot\mu}$

Therefore, we have
$P(X>(1+\delta)\cdot\mu)$
$\leq \frac{E\lbrack e^{t\cdot X}\rbrack}{e^{t\cdot (1+\delta)\cdot\mu}}$
$<\frac {e^{(e^{t}-1)\cdot\mu}}{e^{t\cdot (1+\delta)\cdot\mu}}$
=$e^{((e^{t}-1)-t\cdot (1+\delta))\cdot\mu}$…➀

Next would be to figure out the minimum of $e^{((e^{t}-1)-t\cdot (1+\delta))\cdot\mu}$ by taking its first derivative with respect to $t$, set it to zero, get such value of $t$ to make it zero:
$\frac{\operatorname d{e^{((e^{t}-1)-t\cdot (1+\delta))\cdot\mu}}}{\operatorname d{t}}$
=$\lbrack e^{t}-(1+\delta)\rbrack\cdot\mu\cdot e^{\lbrack (e^{t}-1)-(1+\delta)\cdot t\rbrack\cdot\mu}$

The right side of exponential part won’t be zero, then
$\lbrack e^{t}-(1+\delta)\rbrack\cdot\mu$=$0$
$\Rightarrow e^{t}-(1+\delta)$=$0$
$\Rightarrow t$=$ln(1+\delta)$ could we have the minimum value

Take $t$=$ln(1+\delta)$ into ➀, we get:
$P(X>(1+\delta)\cdot\mu)$<${\lbrack\frac {e^{\delta}}{(1+\delta)^{(1+\delta)}} \rbrack}^{\mu}$…[A]
As a result, $(e^{ln(1+\delta)})^{(1+\delta)\cdot\mu}$=$(1+\delta)^{(1+\delta)\cdot\mu}$

The Lower Bound On Error Probability

It is asking the error probability when target value $X$ is less than the expect value $\mu$, and we’d like to bound it on the lower side.

$P(X<(1-\delta)\cdot\mu)$, for $\delta>0$
=$P(-X>-(1-\delta)\cdot\mu)$
=$P(e^{t\cdot (-X)}>e^{t\cdot (-(1-\delta))\cdot\mu})$, for all $t>0$
$\leq \frac{E\lbrack e^{t\cdot (-X)}\rbrack}{e^{t\cdot (-(1-\delta))\cdot\mu)}}$…Markov inequality

Via similar approach, we could have
$P(X<(1-\delta)\cdot\mu)$<${\lbrack\frac {e^{-\delta}}{(1-\delta)^{(1-\delta)}} \rbrack}^{\mu}$…[B]

Bounding The Bounds

We now have 2 bounds in [A] and [B], such bounds ${\lbrack\frac {e^{\delta}}{(1+\delta)^{(1+\delta)}} \rbrack}^{\mu}$ and ${\lbrack\frac {e^{-\delta}}{(1-\delta)^{(1-\delta)}} \rbrack}^{\mu}$ are difficult to use, we should turn it into human readable format.

The nominator is the exponential raised to the power of $\delta$, take upper bound ${\lbrack\frac {e^{\delta}}{(1+\delta)^{(1+\delta)}} \rbrack}^{\mu}$ for illustration, we’d like to turn $(1+\delta)^{(1+\delta)}$ into exponential powered base expression, to be believed the most efficient way.

[1] The upper bound

Begin from the the natural logarithm of $1+\delta$, that is $ln(1+\delta)$=$y$, then $e^{y}$=$1+\delta$, we can just express $(1+\delta)^{(1+\delta)}$ as $(e^{y})^{(1+\delta)}$, the very next thing would be to figure out $ln(1+\delta)$ in the expression of approximation.

Since $\frac{\operatorname d{ln(1+\delta)}}{\operatorname d{\delta}}$=$\frac {1}{1+\delta}$, the $ln(1+\delta)$ begins from integration:
$ln(1+\delta)$
=$\int_{0}^{1}{\frac {1}{1+\delta}}\operatorname d{\delta}$
=$\int_{0}^{1}{(1-\delta+\delta^{2}-\delta^{3}+\delta^{4}-…)}\operatorname d{\delta}$
=$\delta$-$\frac {\delta^{2}}{2!}$+$\frac {\delta^{3}}{3!}$-$\frac {\delta^{4}}{4!}$+…
=$\sum_{1}^{\infty}(-1)^{k-1}\cdot\frac {\delta^{k}}{k!}$

This $\delta$ is quiet small, temporarily forget about it after the power of 3, then we have
$(1+\delta)^{(1+\delta)}$>$(e^{\delta-\frac {\delta^{2}}{2!}+\frac {\delta^{3}}{3!}})^{(1+\delta)}$
$\;\;\;\;\;\;\;\;\approx e^{\delta+\frac {\delta^{2}}{2}-\frac {\delta^{3}}{6}}$
$\;\;\;\;\;\;\;\;\approx e^{\delta+\frac {\delta^{2}}{2+\varepsilon}}$

Therefore, the upper bound in [A] becomes:
$P(X>(1+\delta)\cdot\mu)$<${\lbrack\frac {e^{\delta}}{(1+\delta)^{(1+\delta)}} \rbrack}^{\mu}$
$\Rightarrow P(X>(1+\delta)\cdot\mu)$<${\lbrack \frac {e^{\delta}}{e^{\delta+\frac {\delta^{2}}{2+\varepsilon}}}\rbrack}^{\mu}$
$\Rightarrow P(X>(1+\delta)\cdot\mu)$<$e^{-\frac {\delta^{2}}{2+\varepsilon}\cdot\mu}$

To be more narrow down, the choice of $e^{-\frac {\delta^{2}}{3}\cdot\mu}$ won’t violect, for $\varepsilon\rightarrow 0$:
$\Rightarrow P(X>(1+\delta)\cdot\mu)$<$e^{-\frac {\delta^{2}}{3}\cdot\mu}$

[2] The lower bound

$ln(1-\delta)$
=$ln(1+(-\delta))$
=$\sum_{1}^{\infty}(-1)^{k-1}\cdot\frac {(-\delta)^{k}}{k!}$

Thus, we have it that
$ln(1-\delta)$=$-\delta-\frac {\delta^{2}}{2!}-\frac {\delta^{3}}{3!}-\frac {\delta^{4}}{4!}-…$
$\Rightarrow ln(1-\delta)$>$-\delta-\frac {\delta^{2}}{2!}$
$\Rightarrow (1-\delta)>e^{-\delta-\frac {\delta^{2}}{2!}}$
$\Rightarrow (1-\delta)^{(1-\delta)}>(e^{-\delta-\frac {\delta^{2}}{2!}})^{(1-\delta)}$
$\Rightarrow (1-\delta)^{(1-\delta)}>e^{-\delta+\frac {\delta^{2}}{2}+\frac {\delta^{3}}{2}}$
$\Rightarrow (1-\delta)^{(1-\delta)}>e^{-\delta+\frac {\delta^{2}}{2}}$, where we ignore the term $\frac {\delta^{3}}{2}$

Therefore, we have the lower bound
$P(X<(1-\delta)\cdot\mu)$<${\lbrack\frac {e^{-\delta}}{(1-\delta)^{(1-\delta)}} \rbrack}^{\mu}$
$\Rightarrow P(X<(1-\delta)\cdot\mu)$<${\lbrack\frac {e^{-\delta}}{e^{-\delta+\frac {\delta^{2}}{2}}} \rbrack}^{\mu}$
$\Rightarrow P(X<(1-\delta)\cdot\mu)$<$e^{-\frac {\delta^{2}}{2}\cdot\mu}$