Model-Based RL Algorithm RMAX - Part 5

22 Apr 2020

Prologue To Model-Based RL Algorithm RMAX - Part 5

This article reviews RMAX in summary of illustration.

Two Main Reinforcement Learning Approaches: Recap

[1] Model-free approachs

They don’t learn a model, model-free approachs learn value function or policy function directly, that is to say they directly estimate state-action value function.

• Q learning
  $Q_{T+1}(S,A)$=$R_{T}(S,A,S^{'})$+$\gamma\cdot max_{A^{'}}Q_{T}(S^{'},A^{'})$
  $\Rightarrow Q_{T+1}^{\ast}(S,A)$=$(1-\alpha)\cdot Q_{T}(S,A)$+$\alpha\cdot Q_{T+1}(S,A)$

• Temporal difference in value function form(without action)

[The rule]

Eposide $T$:
$\;\;$For all $S$, $e(S)$=$0$ at start of eposide, $V_{T}(S)$=$V_{T-1}(S)$
$\;\;$After $S_{t-1}\xrightarrow{r_{t}}S_{t}$:(from step $t-1$ to $t$ with reward $r_{t}$)
$\;\;\;e(S_{t-1})$=$e(S_{t-1})$+$1$:
$\;\;\;\;$Update eligibility of $S_{t-1}$ after arriving to $S_{t}$
$\;\;$For all $S$,
$\;\;V_{T}(S)$=$V_{T-1}(S)$+$\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1}))$
$\;\;\;e(S_{t-1})$=$\lambda\cdot\gamma\cdot e(S_{t-1})$:
$\;\;\;\;$before transite from $S_{t-1}$ to $S_{t}$ in next iteration

• Temporal difference in Q form(with action)
  ➀the Q function takes state and action as input parameters.
  $Q^{\pi}(S_{t},A_{t})$=$E\lbrack R_{t+1}+\gamma\cdot R_{t+2}+\gamma^{2}\cdot R_{t+3}+…\vert S_{t},A_{t}\rbrack$
  ➂take action $A$ to transite from state $S$ to $S’$
  $Q_{T}(S,A)$
  =$Q_{T-1}(S,A)$+$\alpha_{T}\cdot(R(S,A)$+$\gamma\cdot max_{A’}Q_{T-1}(S’,A’)$-$Q_{T-1}(S,A))$
  By repeating above Bellman equation in Q form, the Q value will finally get converged, usually denoted as $Q^{*}(S,A)$, and it’s the policy for you to take action $A$ when you are in state $S$ to get the maximum value.

[2] Model-base approachs

Given sample of data seen so far:
➀build the explicit model of MDP and compute policy for it in the beginning.
➁explore the environment in the given data, learn the transitive probability $P(S,A,S^{'})$ and reward function $R(S,A)$ in accordance to state-action pair.
➂repeat until the transitive probability $P(S,A,S^{'})$ and reward function $R(S,A)$ is to be believed converged to an acceptable confidence interval, during the convergence period, recompute the policy for that state once the transitive probability and reward function has been updated.

One of such approaches is the RMAX algorithm.

RMAX Algorithm Summary

[1] Proceed with explore or exploit

By the given sample of data, this algorithm proceeds with explore to some unknown states or exploit over the same state, and you will never know you are exploring or exploting.

[2] Implicit explore or exploit lemma

After every $T$ steps, you either:
➀achieves or attains the near optimal reward for these $T$ steps.
➁explore to certain unknown state in high probability, learns a little about an unknown state.

[3] The RMAX algorithm

• Initialization
  ➀add the state $S_{0}$ to the MDP model
  ➁set $P(S_{0},A,S)$=$1$ for all state $S$
  ➂set $R(S,A)$=$R_{max}$ for all state $S$ and action $A$
  ➃set all states to unknown states, excepts for $S_{0}$
  ➄set all visited counter of state-action pairs to $0$
  

• Repeat
  ➀compute a $T$-step policy for current state $S$ and execute it
  ➁for any visited state-action pair, keep track of its count and reward with respect to state transition from $S$ to $S^{'}$
  ➂if the same state-action pair has been visited over enough times to estimate $P(S,A,S^{'})$ and $R(S,A)$, update the transitive probability, turn the state-action pair from unknown to know, and repeat from ➀
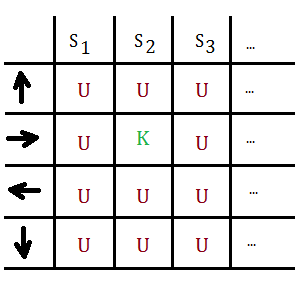
  ➃loops through ➀,➁,➃ until all states has become known

[4] How many times are enough?

• By Chernoff Bounds For Bernoulli Random Variable
  We have $P(\sum_{i=1}^{n}Z_{i}>a)<e^{-\frac {a^{2}}{2\cdot n}}$, where $Z_{1}$,$Z_{2}$,…,$Z_{n}$ are the $n$ distinct independent trials on state $G_{i}$, and $a$ is the error term, such inequality bounds the error probability by $e^{-\frac {a^{2}}{2\cdot n}}$ that after $n$ independent trials on state $G_{i}$, the total estimate bias is greater than the error term $a$.

[5] Put it all together

With probability at least $1-\delta$, the RMAX algorithm will reach $\varepsilon$ close to optimal policy, in time polinomial in the number of states, the number of actions, $\frac {1}{\delta}$, $\frac {1}{\varepsilon}$.

• Every $T$ steps
  By implicit explore or exploit lemma:
  ➀achieve near optimal reward, or
  ➁explore to certain unknown state with high probability. Since the number of states and actions are finite, it wouldn’t take too long before all states turn into known!

Addendum

➀R-max: A General Polynomial Time Algorithm for Near-Optimal Reinforcement Learning, Ronen I. Brafman, CS in Ben-Gurion University, Moshe Tennenholtz, CS in Stanford University
➁Reinforcement Learning: Machine Learning - CSE446, Carlos Guestrin, University of Washington, June 5, 2013