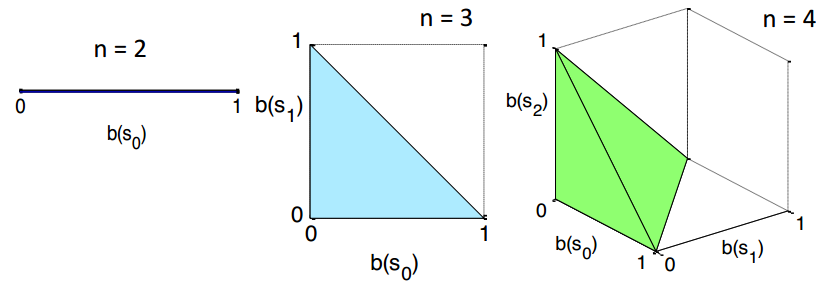Partial Observable Markov Decision Process - Part 2
13 Aug 2020Prologue To Partial Observable Markov Decision Process - Part 2
The Real World Is Almost Partially Observable
Regular MDP
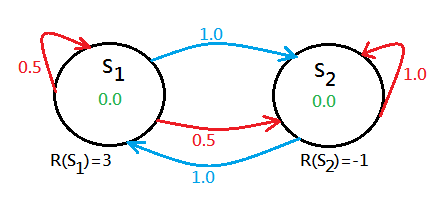
When we are in the regular MDP, the agent observes the state of the environment, it can make full observation. The chess grid and the 2 states examples exhibit the environment of the regular MDP.
➀Markov Decision Process In Stochastic Environment
➁Markov Decision Process To Seek The Optimal Policy
- Partially Observable MDP
If we are in the partially observable environment, the agent can't observe the full world state, but the observation gives hint about true state.
➀the agent has no idea about the world state, what’s behind the door, where am I.
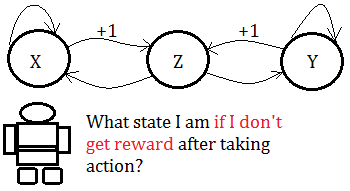
➁the agent don’t know what state he is in if he didn’t get reward after taking action.
- Types of partial observability
➀the sensor(some component of the agent) might have measurement fail due to noise.
➁multiple states might give the same observation, i.e., what’s behind the door, what state the agent is in after taking action without reward.
Policies Under POMDP?
[Question]Should we use policy mapping state to action in POMDP?
[Answer]Before we step any further, it strikes on our head that:
➀the agent only gets some(partial) observations
➁no more Markovian signal(the state) directly available to the agentWe should use all information obtained, the full history of observations, by doing the belief update.
Hints On Belief Update
[1] CalculationPOMDP is often given an initial belief:
➀we are given an initial probability distribution over states in the departure point.
➁we shhould keep track of how this initial probability distribution over states changes from initial point to the next step.
➂by the already known prior belief $b$, the action taken $A$, the observation thus made $O$, to figure out the new next belief $b^{'}$.This process is called the belief update.
[2] Apply the Bayer's rule➀begin from the Bayes Theorem:
$P(B\vert A)$=$\frac {P(A\vert B)\cdot P(B)}{P(A)}$
➁substitute the relevant variables:
$P(S^{'}\vert O)$=$\frac {P(O\vert S^{'})\cdot P(S^{'})}{P(O)}$
➂add the action $A$ and prior belief $b$ in the given:
$P(S^{'}\vert O,A,b)$=$\frac {P(O\vert S^{'},A,b)\cdot P(S^{'}\vert A,b)}{P(O\vert A,b)}$
➃expand $P(S^{'}\vert A,b)$ and $P(O\vert A,b)$
$P(S^{'}\vert O,A,b)$
=$\frac {P(O\vert S^{'},A,b)\cdot P(S^{'}\vert A,b)}{P(O\vert A,b)}$
=$\frac {P(O\vert S^{'},A,b)\cdot \sum_{S}P(S^{'}\vert A,S)\cdot b(S)}{\sum_{S^{''}}P(O|S^{''})\cdot\sum_{S}P(S^{''}|A,S)\cdot b(S)}$
Full Illustration Of Belief Update In Tiger Problem
[1] The tiger problem
[2] What decision should we make?
The given condition
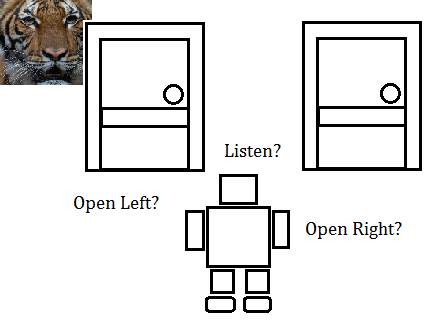
➀suppose you(the agent) are standing in front of 2 doors, there is a tiger behind one of the 2 doors, that is to say the world states are tiger is behind the left or right door.
➁there are 3 actions, listen, open left door and open right door.
➂listen is not free and might get inaccurate information.
➃when you open the wrong door, you will get eaten by tiger, the reward is $-100$.
➄if you open the right door, you will get $+10$ as the reward.
➅you will get $-1$ after each listen.Transitive probability
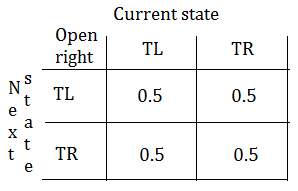
➀by listening, the tiger stays where it is.
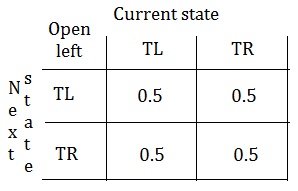
➁when you open the left door, the tiger has $50%$ to stay behind the left door, or $50%$ to stay behind the right door.
➂when you open the right door, the tiger has $50%$ to stay behind the right door, or $50%$ to stay behind the left door.
Observation and its probability
➀when listening, if the world state is tiger left, by this given, we hear tiger left, such probability is [a]$P(HL\vert TL,listen,b)$=$0.85$, while we still have [b]$P(HR\vert TR,listen,b)$=$0.15$ for we hear tiger right, given that tiger is right(we think tiger is right) under the world state tiger left.
The probability [c]$P(HR\vert TR,listen,b)$=$0.85$ for we hear tiger right, given that the world state is tiger right, while there exists probability [d]$P(HL\vert TL,listen,b)$=$0.15$ for we hear tiger left, given that tiger is left under the world state tiger right.
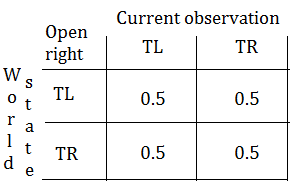
➁when opening the left door, below exhibits the observation probability given the world state is tiger left and right respectively.
➂when opening the right door, below exhibits the observation probability given the world state is tiger left and right respectively.
Before we make a decision to open the correct door, we should have gathered sufficient information pertaining to the possible changes of probability distribution of tiger’s location, that’s to keep track of the belief history.
Reinforcement learning is to learn the model and planning.Suppose the model is of no question in this example of tiger problem, we need to maintain a list of all possibilities of the belief changes, such history is build by listening in each step.
[3] Belief update::mjtsai1974By listening in each step, we can gather information of tiger location, that’s the belief, based on history of such belief, we can then have a plan, i.e, the action to take after HL$\rightarrow$HL, HL$\rightarrow$HR.
Notes::mjtsai1974
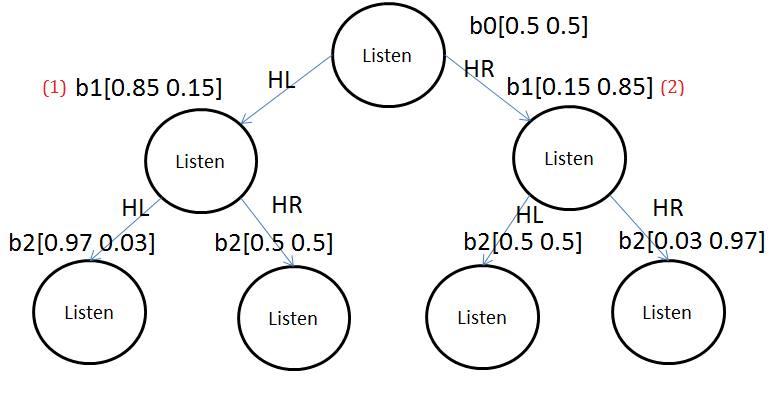
Begin from initial point
We are given the tiger is at left and right with each probability $50%$ respectively, that’s $b_{0}\lbrack 0.5\;0.5\rbrack$, the first $0.5$ is the probability for tiger at left side, the similarity for tiger at the right side.From init$\rightarrow$HL
Given that you are hearning tiger left, we’d like to calculate the belief at this moment.
➀$b_{1}(TL)$
=$P(TL\vert HL,listen,b_{0})$
=$\frac {P(HL\vert TL,listen,b_{0})\cdot P(TL\vert listen,b_{0})}{P(HL\vert listen,b_{0})}$
=$\frac {P(HL\vert TL,listen,b_{0})\cdot\sum_{S}P(TL\vert listen,S)\cdot b_{0}(S)}{\sum_{S^{''}}P(HL\vert listen,S^{''})\cdot\sum_{S^{'}}P(S^{''}\vert listen,S^{'})\cdot b_{0}(S^{'})}$
=$\frac {0.85\cdot(1\cdot 0.5+0\cdot 0.5)}{0.85\cdot(1\cdot 0.5+0\cdot 0.5)+0.15\cdot(1\cdot 0.5+0\cdot 0.5)}$
=$0.85$
$\Rightarrow$We are now asking for belief state of tiger left, given that we are hearing left, thus the likeli should be the probability that we hear tiger left given that tiger is left, multiply by probability of tiger left, given from the prior belief state of tiger left(and by listen), divided by the total probability that we make the observation of hearing tiger left.
$\Rightarrow$The total probability of hearing tiger left is summing over all states($S^{''}$), the probability of hearing tiger left given that the tiger state is $S^{''}$, in turn multiply by summing over the state $S^{'}$, the transitive probabilities from $S^{'}$ to $S^{''}$ by listening, finally multiply with the prior belief, the probability that the world state is $S^{'}$.
➁$b_{1}(TR)$
=$P(TR\vert HR,listen,b_{0})$
=$\frac {P(HR\vert TR,listen,b_{0})\cdot P(TR\vert listen,b_{0})}{P(HR\vert listen,b_{0})}$
=$\frac {P(HR\vert TR,listen,b_{0})\cdot\sum_{S}P(TR\vert listen,S)\cdot b_{0}(S)}{\sum_{S^{''}}P(HR\vert listen,S^{''})\cdot\sum_{S^{'}}P(S^{''}\vert listen,S^{'})\cdot b_{0}(S^{'})}$
=$\frac {0.15\cdot(0\cdot 0.5+1\cdot 0.5)}{0.15\cdot(0\cdot 0.5+1\cdot 0.5)+0.85\cdot(0\cdot 0.5+1\cdot 0.5)}$
=$0.15$
$\Rightarrow$we have belief updated from $b_{0}$ to $b_{1}\lbrack 0.85\;0.15\rbrack$ in this brach.
From init$\rightarrow$HR
Given that you are hearning tiger right, we’d like to calculate the belief at this moment.
➀$b_{1}(TL)$
=$P(TL\vert HL,listen,b_{0})$
=$\frac {0.15\cdot(1\cdot 0.5+0\cdot 0.5)}{0.15\cdot(1\cdot 0.5+0\cdot 0.5)+0.85\cdot(1\cdot 0.5+0\cdot 0.5)}$
=$0.15$
➁$b_{1}(TR)$
=$P(TR\vert HR,listen,b_{0})$
=$\frac {0.85\cdot(0\cdot 0.5+1\cdot 0.5)}{0.85\cdot(0\cdot 0.5+1\cdot 0.5)+0.1\cdot(0\cdot 0.5+1\cdot 0.5)}$
=$0.85$
$\Rightarrow$we have belief updated from $b_{0}$ to $b_{1}\lbrack 0.15\;0.85\rbrack$ in this brach.From init$\rightarrow$HL$\rightarrow$HL
Suppose that you are hearning tiger left after hearing tiger left, we’d like to calculate the belief at this moment.
➀$b_{2}(TL)$
=$P(TL\vert HL,listen,b_{1})$
=$\frac {0.85\cdot(1\cdot 0.85+0\cdot 0.15)}{0.85\cdot(1\cdot 0.85+0\cdot 0.15)+0.15\cdot(1\cdot 0.15+0\cdot 0.85)}$
=$0.967986$
$\approx 0.97$
➁$b_{2}(TR)$
=$P(TR\vert HR,listen,b_{1})$
=$\frac {0.15\cdot(0\cdot 0.85+1\cdot 0.15)}{0.15\cdot(0\cdot 0.85+1\cdot 0.15)+0.85\cdot(0\cdot 0.15+1\cdot 0.85)}$
=$0.03020$
$\approx 0.03$
$\Rightarrow$we have belief updated from $b_{1}\lbrack 0.85\;0.15\rbrack$ to $b_{2}\lbrack 0.97\;0.03\rbrack$ in this brach.
From init$\rightarrow$HL$\rightarrow$HR
Suppose that you are hearning tiger left after hearing tiger right, we’d like to calculate the belief at this moment.
➀$b_{2}(TL)$
=$P(TL\vert HL,listen,b_{1})$
=$\frac {0.15\cdot(1\cdot 0.85+0\cdot 0.15)}{0.15\cdot(1\cdot 0.85+0\cdot 0.15)+0.85\cdot(1\cdot 0.15+0\cdot 0.85)}$
=$0.5$
➁$b_{2}(TR)$
=$P(TR\vert HR,listen,b_{1})$
=$\frac {0.85\cdot(0\cdot 0.85+1\cdot 0.15)}{0.85\cdot(0\cdot 0.85+1\cdot 0.15)+0.15\cdot(0\cdot 0.15+1\cdot 0.85)}$
=$0.5$
$\Rightarrow$we have belief updated from $b_{1}\lbrack 0.85\;0.15\rbrack$ to $b_{2}\lbrack 0.5\;0.5\rbrack$ in this brach.The likeli in the nominator is goint to use the belief distribution at the node which it is branching from as the prior.
[4] Have a tea break before opening the door
From init$\rightarrow$HR$\rightarrow$HL
Suppose that you are hearning tiger left after hearing tiger right, we’d like to calculate the belief at this moment.
➀$b_{2}(TL)$
=$P(TL\vert HL,listen,b_{1})$
=$\frac {0.85\cdot(1\cdot 0.15+0\cdot 0.85)}{0.85\cdot(1\cdot 0.15+0\cdot 0.85)+0.15\cdot(1\cdot 0.85+0\cdot 0.15)}$
=$0.5$
➁$b_{2}(TR)$
=$P(TR\vert HR,listen,b_{1})$
=$\frac {0.15\cdot(0\cdot 0.15+1\cdot 0.85)}{0.15\cdot(0\cdot 0.15+1\cdot 0.85)+0.85\cdot(0\cdot 0.85+1\cdot 0.15)}$
$0.5$
$\Rightarrow$we have belief updated from $b_{1}\lbrack 0.15\;0.85\rbrack$ to $b_{2}\lbrack 0.5\;0.5\rbrack$ in this brach.From init$\rightarrow$HR$\rightarrow$HR
Suppose that you are hearning tiger right after hearing tiger right, we’d like to calculate the belief at this moment.
➀$b_{2}(TL)$
=$P(TL\vert HL,listen,b_{1})$
=$\frac {0.15\cdot(1\cdot 0.15+0\cdot 0.85)}{0.15\cdot(1\cdot 0.15+0\cdot 0.85)+0.85\cdot(1\cdot 0.85+0\cdot 0.15)}$
$\approx 0.03$
➁$b_{2}(TR)$
=$P(TR\vert HR,listen,b_{1})$
=$\frac {0.85\cdot(0\cdot 0.15+1\cdot 0.85)}{0.85\cdot(0\cdot 0.15+1\cdot 0.85)+0.15\cdot(0\cdot 0.85+1\cdot 0.15)}$
=$\approx 0.97$
$\Rightarrow$we have belief updated from $b_{1}\lbrack 0.15\;0.85\rbrack$ to $b_{2}\lbrack 0.03\;0.97\rbrack$ in this brach.Making belief update over theses steps, we can do some plan on the belief histroy, if we make continuous 2 observations of hearing tiger left, the belief would be the probability distribution over tiger left and tiger right, which is $b_{2}\lbrack 0.97\;0.03\rbrack$. Should we open the right door??
The ideal answer would be discusssed in my next article.
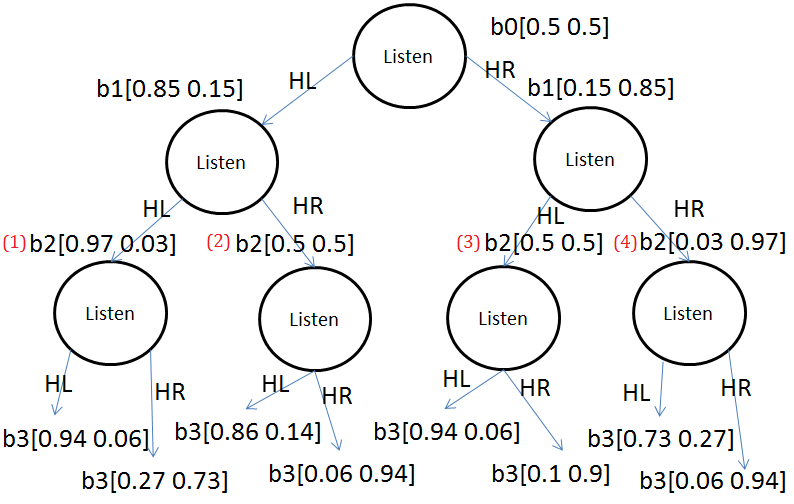
[5] Make extra one step
From init$\rightarrow$HL$\rightarrow$HL$\rightarrow$HL
Guess what, if we keep on following in this path, from init to hearning tiger left, next to hearing tiger left, next to hearing tiger left, we’d like to make the belief update at this moment.
➀$b_{3}(TL)$
=$P(TL\vert HL,listen,b_{2})$
=$\frac {0.85\cdot\lbrack(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)\rbrack}{0.85\cdot\lbrack(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)\rbrack+0.15\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.03+0\cdot 0.97)\rbrack}$
$\approx 0.94$
➁$b_{3}(TR)$
=$P(TR\vert HR,listen,b_{2})$
=$\frac {0.15\cdot\lbrack(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)\rbrack}{0.15\cdot\lbrack(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)\rbrack+0.85\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack}$
$\approx 0.06$
$\Rightarrow$we have belief updated from $b_{2}\lbrack 0.97\;0.03\rbrack$ to $b_{3}\lbrack 0.94\;0.06\rbrack$ in this brach.
From init$\rightarrow$HL$\rightarrow$HL$\rightarrow$HR
Go from init to hearning tiger left, next to hearing tiger left, next to hearing tiger right, we’d like to make the belief update at this moment.
➀$b_{3}(TL)$
=$P(TL\vert HL,listen,b_{2})$
=$\frac {0.15\cdot\lbrack(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.03+0\cdot 0.97)\rbrack}{0.15\cdot\lbrack(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.03+0\cdot 0.97)\rbrack+0.85\cdot(1\cdot 0.5+0\cdot 0.5)}$
=$0.3463$
➁$b_{3}(TR)$
=$P(TR\vert HR,listen,b_{2})$
=$\frac {0.85\cdot\lbrack(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack}{0.85\cdot\lbrack(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack+0.15\cdot(0\cdot 0.5+1\cdot 0.5)}$
=$0.9444$
$\Rightarrow$The $b_{3}(TL)$+$b_{3}(TR)$ not equal to $1$, we are encounter a big problem, guess what? By normalization, we can get the correct answer.
➂$N(b_{3}(TL))$=$\frac {0.3463}{0.3463+0.9444}$=$0.268217$
➃$N(b_{3}(TR))$=$\frac {0.9444}{0.3463+0.9444}$=$0.73169$
$\Rightarrow$we have belief updated from $b_{2}\lbrack 0.97\;0.03\rbrack$ to $b_{3}\lbrack 0.27\;0.73\rbrack$ in this brach.From init$\rightarrow$HL$\rightarrow$HR$\rightarrow$HL
Go from init to hearning tiger left, next to hearing tiger right, next to hearing tiger left, we’d like to make the belief update at this moment.
➀$b_{3}(TL)$
=$P(TL\vert HL,listen,b_{2})$
=$\frac {0.85\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)\rbrack}{0.85\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)\rbrack+0.15\cdot(1\cdot 0.03+0\cdot 0.97)}$
$\approx 0.997$
➁$b_{3}(TR)$
=$P(TR\vert HR,listen,b_{2})$
=$\frac {0.15\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)\rbrack}{0.15\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)\rbrack+0.85\cdot(0\cdot 0.03+1\cdot 0.97)}$
$\approx 0.158$
➂$N(b_{3}(TL))$=$\frac {0.997}{0.997+0.158}$=$0.863$
➃$N(b_{3}(TR))$=$\frac {0.158}{0.997+0.158}$=$0.137$
$\Rightarrow$we have belief updated from $b_{2}\lbrack 0.5\;0.5\rbrack$ to $b_{3}\lbrack 0.86\;0.14\rbrack$ in this brach.From init$\rightarrow$HL$\rightarrow$HR$\rightarrow$HR
Go from init to hearning tiger left, next to hearing tiger right, next to hearing tiger right, we’d like to make the belief update at this moment.
➀$b_{3}(TL)$
=$P(TL\vert HL,listen,b_{2})$
=$\frac {0.15\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.03+0\cdot 0.97)\rbrack}{0.15\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.03+0\cdot 0.97)\rbrack+0.85\cdot\lbrack(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)\rbrack}$
=$0.0598194131$
$\approx 0.06$
➁$b_{3}(TR)$
=$P(TR\vert HR,listen,b_{2})$
=$\frac {0.85\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack}{0.85\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack+0.15\cdot\lbrack(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)\rbrack}$
=$0.94$
$\Rightarrow$we have belief updated from $b_{2}\lbrack 0.5\;0.5\rbrack$ to $b_{3}\lbrack 0.06\;0.94\rbrack$ in this brach.From init$\rightarrow$HR$\rightarrow$HL$\rightarrow$HL
Go from init to hearning tiger right, next to hearing tiger left, next to hearing tiger left, we’d like to make the belief update at this moment.
➀$b_{3}(TL)$
=$P(TL\vert HL,listen,b_{2})$
=$\frac {0.85\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.97+0\cdot 0.03)\rbrack}{0.85\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.97+0\cdot 0.03)\rbrack+0.15\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.03+0\cdot 0.97)\rbrack}$
$\approx 0.94$
➁$b_{3}(TR)$
=$P(TR\vert HR,listen,b_{2})$
=$\frac {0.15\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.97+1\cdot 0.03)\rbrack}{0.15\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.97+1\cdot 0.03)\rbrack+0.85\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack}$
$\approx 0.06$
$\Rightarrow$we have belief updated from $b_{2}\lbrack 0.5\;0.5\rbrack$ to $b_{3}\lbrack 0.94\;0.06\rbrack$ in this brach.From init$\rightarrow$HR$\rightarrow$HL$\rightarrow$HR
➀$b_{3}(TL)$
=$P(TL\vert HL,listen,b_{2})$
=$\frac {0.15\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.03+0\cdot 0.97)\rbrack}{0.15\cdot\lbrack(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.03+0\cdot 0.97)\rbrack+0.85\cdot\lbrack(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)\rbrack}$
$\approx 0.11$
➁$b_{3}(TR)$
=$P(TR\vert HR,listen,b_{2})$
=$\frac {0.85\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack}{0.85\cdot\lbrack(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack+0.15\cdot(0\cdot 0.97+1\cdot 0.03)}$
$\approx 0.9913$
➂$N(b_{3}(TL))$=$\frac {0.11}{0.11+0.9913}$=$0.099\approx 0.1$
➃$N(b_{3}(TR))$=$\frac {0.9913}{0.11+0.9913}$=$0.9$
$\Rightarrow$we have belief updated from $b_{2}\lbrack 0.5\;0.5\rbrack$ to $b_{3}\lbrack 0.1\;0.9\rbrack$ in this brach.From init$\rightarrow$HR$\rightarrow$HR$\rightarrow$HL
➀$b_{3}(TL)$
=$P(TL\vert HL,listen,b_{2})$
=$\frac {0.85\cdot\lbrack(1\cdot 0.03+0\cdot 0.97)+(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.97+0\cdot 0.03)\rbrack}{0.85\cdot\lbrack(1\cdot 0.03+0\cdot 0.97)+(1\cdot 0.5+0\cdot 0.5)+(1\cdot 0.97+0\cdot 0.03)\rbrack+0.15\cdot(1\cdot 0.5+0\cdot 0.5)}$
$\approx 0.9444$
➁$b_{3}(TR)$
=$P(TR\vert HR,listen,b_{2})$
=$\frac {0.15\cdot\lbrack(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack}{0.15\cdot\lbrack(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)+(0\cdot 0.03+1\cdot 0.97)\rbrack+0.85\cdot(0\cdot 0.5+1\cdot 0.5)}$
$\approx 0.3461538$
➂$N(b_{3}(TL))$=$\frac {0.9444}{0.94444+0.3461538}$=$0.7317\approx 0.73$
➃$N(b_{3}(TR))$=$\frac {0.3461538}{0.94444+0.3461538}$=$0.268221\approx 0.27$
$\Rightarrow$we have belief updated from $b_{2}\lbrack 0.03\;0.97\rbrack$ to $b_{3}\lbrack 0.73\;0.27\rbrack$ in this brach.From init$\rightarrow$HR$\rightarrow$HR$\rightarrow$HR
➀$b_{3}(TL)$
=$P(TL\vert HL,listen,b_{2})$
=$\frac {0.15\cdot\lbrack(1\cdot 0.03+0\cdot 0.97)+(1\cdot 0.5+0\cdot 0.5)\rbrack}{0.15\cdot\lbrack(1\cdot 0.03+0\cdot 0.97)+(1\cdot 0.5+0\cdot 0.5)\rbrack+0.85\cdot\lbrack(1\cdot 0.97+0\cdot 0.03)+(1\cdot 0.5+0\cdot 0.5)\rbrack}$
=$0.0598$
$\approx 0.06$
➁$b_{3}(TR)$
=$P(TR\vert HR,listen,b_{2})$
=$\frac {0.85\cdot\lbrack(0\cdot 0.03+1\cdot 0.97)+(0\cdot 0.5+1\cdot 0.5)\rbrack}{0.85\cdot\lbrack(0\cdot 0.03+1\cdot 0.97)+(0\cdot 0.5+1\cdot 0.5)\rbrack+0.15\cdot\lbrack(0\cdot 0.97+1\cdot 0.03)+(0\cdot 0.5+1\cdot 0.5)\rbrack}$
=$0.9401$
$\approx 0.94$
$\Rightarrow$we have belief updated from $b_{2}\lbrack 0.03\;0.97\rbrack$ to $b_{3}\lbrack 0.06\;0.94\rbrack$ in this brach.
Belief Space
Belief is a probability distribution over states.
➀$\sum_{S}b(S)$=$1$
➁for $n$ states, belief has $n-1$ degree of freedom
➂belief lives in a $n-1$ dimensional simplex, i.e, a world of 2 states, $b(S_{0})$ is determined by the value of $b(S_{1})$, it has 1 degree of freedom. i.e, a world of 3 states, $b(S_{i})$ is determined by the other 2 values, it has 2 degree of freedom.
Addendum
➀Partial Observable Markov Decision Process, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
➁Decsision Making in Intellingent Systems: POMDP, 14 April 2008, Frans Oliehoek
➂Intro to POMDPs, CompSci 590.2 Reinforcement Learning