Partial Observable Markov Decision Process - Part 4

04 Dec 2020

Prologue To Partial Observable Markov Decision Process - Part 4

This post will explain why PWLC works and how it is aggregated in value iteration of POMDP(Partial Observable Markov Decision Process).

Recap POMDP Value Iteration

• Basic idea in POMDP value iteration
  ➀calculate value function vectors for each action with regard to observation thus made in horizon $1$.
  ➁continue looking forward horizon $2$,$3$,…
  ➂make such value iteration until convergence

• The PWLC(piecewise linear convex)
  The value function of POMDP can be represented as max of linear segments - PWLC.
  $\left(1\right)$convexity:
  state is known at the edges of belief space
  $\left(2\right)$linear segments:
  ➀linear function in the format of belief $\times$ reward
  ➁segments in horizon 1 are linear
  ➂segments in horizon $n$ are linear combination of horizon $n-1$'s segments

Illustration: Why And How PWLC Works?

In this section, I am going to lead you to the reason to why PWLC takes effect, and guide you through the way it is aggregated to a convergence.

The value function of POMDP can be represented as max of linear segments - PWLC could be expressed:
$V_{t}(b)$
=$max_{\alpha\in\tau_{t}}\alpha\cdot b$
=$max_{\alpha\in\tau_{t}}\sum_{s}\alpha(s)\cdot b(s)$

[Question]

Assume we have $\tau_{t-1}$ such that $V_{t-1}(b)$=$max_{\alpha\in\tau_{t-1}}\alpha\cdot b$, you are ask to build $\tau_{t}$ such that $V_{t}(b)$=$max_{\alpha\in\tau_{t}}\alpha\cdot b$

[Answer]

• proof::part-1
  ➀$V_{t}(b)$=$max_{a\in A}V_{t}^{a}(b)$
  $\Rightarrow V_{t}^{a}(b)$=$\sum_{o}V_{t}^{a,o}(b)$
  $\Rightarrow V_{t}^{a,o}(b)$=$\sum_{s}R(s,a)\cdot\frac {b(s)}{\left|o\right|}$+$\gamma\cdot P(o\vert b,a)\cdot V_{t-1}(S.E(b,a,o))$
  , where we have
  $V_{t-1}(S.E(b,a,o))$
  =$max_{\alpha\in\tau_{t-1}}\sum_{s^{'}}\alpha(s^{'})\cdot\frac {P(o\vert s^{'},a)\cdot\sum_{s}P(s^{'}\vert s,a)\cdot b(s)}{P(o\vert b,a)}$
  ➁although $V_{t-1}(S.E(b,a,o))$ is highly non-linear, its awasome denominator part of $P(o\vert b,a)$ could be safely eliminated and tossed out, thus we are left with a linear transformation from $V_{t}^{a,o}(b)$ to its next $V_{t-1}(S.E(b,a,o))$, and $S.E(b,a,o)$=$b^{'}$, which strongly supports value function transformation in Illustration Of PWLC(Piecewise Linear Convex) in POMDP - Part 3.

• proof::part-2
  Succeeding to part-1,
  $\tau_{t}$=$U_{a}\tau_{t}^{a}$
  $\tau_{t}^{a}$=$\oplus\tau_{t}^{a,o}$
  $\Leftrightarrow V_{t}^{a}(b)$=$\sum_{o}V_{t}^{a,o}(b)$
  , where we have
  ➀finite state space, action space, observation space
  ➁$\left|A\right|\times\left|O\right|$ could be quiet big, but, it is finite.
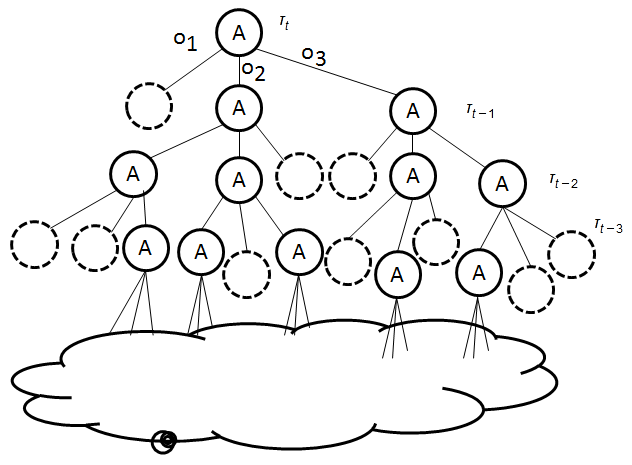
  ➂$\left|\tau_{t}\right|$ could grow up doubly, exponentially with $t$, but, it is finite.

We have $\left|\tau_{t}\right|$=$\left|\tau_{t-1}\right|^{\left|O\right|}\times\left|A\right|$

$\tau_{t}$ is derived from the vectors of optimal actions, associated with the dedicated observation in $\tau_{t-1}$.

The POMDP Value Iteration Drawbacks

➀time complexity is exponential in actions and observations.
➁dimensionality of belief space grows with state numbers.
➂exponential growth with number of iterations.

Hugely intractable to solve optimality, value iteration aims for small POMDP problems.

Addendum

➀Partial Observable Markov Decision Process, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
➁POMDP Value Iteration Example, Tony, Brown University’s Computer Science Department
➂POMDP Tutorial, Stefan Kopp, Bielefeld University
➃Partially Observable Markov Decision Process, Geoff Hollinger, 2007 fall
➄POMDPOs, Rowan McAllister and Alexandre Navarro, MLG Reading Group, 02 June 2016, Cambridge University