QR Decomposition

31 Oct 2017

QR Decomposition

QR decomposition claims that A = B⋅X = B⋅D⋅E⋅X = Q⋅R. This article will show you the way to prove it, we will begin from Gram-Schmit Procedure, then, briefly introduce to the projection matrix, then, migrate to triangular matrix, finally to prove the QR decomposition.

Gram-Schmit Procedure

Given a set of linear independent vectors set S = {v₁, v₂,…, v_p} ∈ R^m,
define vectors u_i, 1 ≤ i ≤ p by
u_i = v_i − [((v_i)^t ⋅ u₁) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁ − [((v_i)^t ⋅ u₂) ∕ ((u₂)^t ⋅ u₂)] ⋅ u₂ − [((v_i)^t ⋅ u₃) ∕ ((u₃)^t ⋅ u₃)] ⋅ u₃ − … − [((v_i)^t ⋅ u_i−1) ∕ ((u_i−1)^t ⋅ u_i−1)] ⋅ u_i−1
the set T = {u₁, u₂,…, u_p} is a linear independent orthonormal set and aoan(S) = span(T)
we just have below holds:
u₁ = v₁
u₂ = v₂ − [((v₂)^t ⋅ u₁) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁
u₃ = v₃ − [((v₃)^t ⋅ u₁) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁ − [((v₃)^t ⋅ u₂) ∕ ((u₂)^t ⋅ u₂)] ⋅ u₂
u₄ = v₄ − [((v₄)^t ⋅ u₁) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁ − [((v₄)^t ⋅ u₂) ∕ ((u₂)^t ⋅ u₂)] ⋅ u₂ − [((v₄)^t ⋅ u₃) ∕ ((u₃)^t ⋅ u₃)] ⋅ u₃
…
u_p = v_p − [((v_p)^t ⋅ u₁) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁ − [((v_p)^t ⋅ u₂) ∕ ((u₂)^t ⋅ u₂)] ⋅ u₂ − … − [((v_p)^t ⋅ u_p−1) ∕ ((u_p−1)^t ⋅ u_p−1)] ⋅ u_p−1

Prove Gram-Schmit Procedure by means of Projection Matrix

Begin by projection matrix to prove Gram-Schmit Procedure illustrated in below pic:

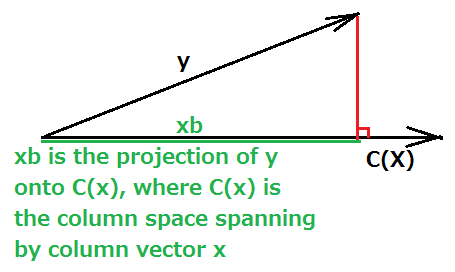
take x ⋅ b = y_proj, the projection of y onto C(x), where C(x) is the column space spanned by vector x
C(x) ⊥ (y − x ⋅ b), then
=>C(x) ⋅ (y − x ⋅ b) = 0,
=>x^t ⋅ (y − x ⋅ b) = 0,
=>x^t ⋅ x ⋅ b = x^t ⋅ y,
=>b = (x^t ⋅ x)⁻ ⋅ x^t ⋅ y; where (x^t ⋅ x)⁻ is the generalized inverse form,
=>y_proj = x ⋅ (x^t ⋅ x)⁻ ⋅ x^t ⋅ y
∵x is itself a column vector, then (x^t ⋅ x)⁻ = (x^t ⋅ x)⁻¹ just holds, for the vector x is in the spanning set/basis
∴y_proj = [(x^t ⋅ y) ∕ (x^t ⋅ x)] ⋅ x = [(y^t ⋅ x) ∕ (x^t ⋅ x)] ⋅ x

To further explain Gram-Schmit Procedure in terms of Projection Matrix:

take y as v₂, x as u₁, where u₁ = v₁, then
u₂ = v₂ − [((u₁)^t ⋅ v₂) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁, where the second term is just the projection of v₂ onto u₁
u₃ = v₃ − Proj_w2(v₃), where w₂ = Span(u₁, u₂)
     = v₃ − Proj_u1(v₃) − Proj_u2(v₃)
     = v₃ − [((u₁)^t ⋅ v₃) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁ − [((u₂)^t ⋅ v₃) ∕ ((u₂)^t ⋅ u₂)] ⋅ u₂
the flow is exhibited by below pic:

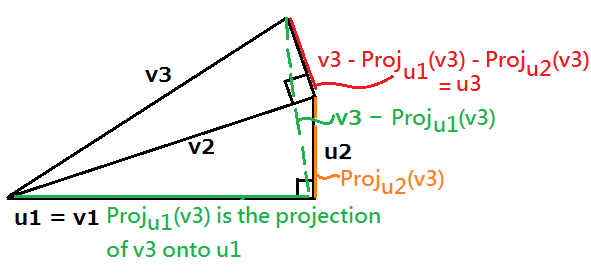
u₄ = v₄ − Proj_w3(v₄), where w₃ = Span(u₁, u₂, u₃)
     = v₄ − [((u₁)^t ⋅ v₄) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁ − [((u₂)^t ⋅ v₄) ∕ ((u₂)^t ⋅ u₂)] ⋅ u₂ − [((u₃)^t ⋅ v₄) ∕ ((u₃)^t ⋅ u₃)] ⋅ u₃
…
finally, we can reach
u_p = v_p − [((u₁)^t ⋅ v_p) ∕ ((u₁)^t ⋅ u₁)] ⋅ u₁ − [((u₂)^t ⋅ v_p) ∕ ((u₂)^t ⋅ u₂)] ⋅ u₂ − … − [((u_p−1)^t ⋅ v_p) ∕ ((u_p−1)^t ⋅ u_p−1)] ⋅ u_p−1

Further refine the notation in Gram-Schmit and Formula Representation:

take S = {v₁, v₂,…, v_p} to be S = {a₁, a₂,…, a_p}
take T = {u₁, u₂,…, u_p} to be T = {b₁, b₂,…, b_p}
b₁ = a₁
b₂ = a₂ − [((b₁)^t ⋅ a₂) ∕ ((b₁)^t ⋅ b₁)] ⋅ b₁
b₃ = a₃ − [((b₁)^t ⋅ a₃) ∕ ((b₁)^t ⋅ b₁)] ⋅ b₁ − [((b₂)^t ⋅ a₃) ∕ ((b₂)^t ⋅ b₂)] ⋅ b₂
b₄ = a₄ − [((b₁)^t ⋅ a₄) ∕ ((b₁)^t ⋅ b₁)] ⋅ b₁ − [((b₂)^t ⋅ a₄) ∕ ((b₂)^t ⋅ b₂)] ⋅ b₂ − [((b₃)^t ⋅ a₄) ∕ ((b₃)^t ⋅ b₃)] ⋅ b₃
…
b_p = a_p − [((b₁)^t ⋅ a_p) ∕ ((b₁)^t ⋅ b₁)] ⋅ b₁ − [((b₂)^t ⋅ a_p) ∕ ((b₂)^t ⋅ b₂)] ⋅ b₂ − [((b₃)^t ⋅ a_p) ∕ ((b₃)^t ⋅ b₃)] ⋅ b₃ − … − [((b_p−1)^t ⋅ a_p) ∕ ((b_p−1)^t ⋅ b_p−1)] ⋅ b_p−1
At this moment, the proof has validated Gram-Schmit by the projection matrix

Express Gram-Schmit Procedure in Matrix Product

Advance one step to represent Gram-Schmit Procedure by matrix product:

if we take X_i,j = ((b_i)^t ⋅ a_j) ∕ ((b_i)^t ⋅ b_i), then, we could have:
b₁ = a₁
b₂ = a₂ − X_1,2 ⋅ b₁
b₃ = a₃ − X_1,3 ⋅ b₁ − X_2,3 ⋅ b₂
b₄ = a₄ − X_1,4 ⋅ b₁ − X_2,4 ⋅ b₂ − X_3,4 ⋅ b₃
…
b_p = a_p − X_1,p ⋅ b₁ − X_2,p ⋅ b₂ − X_3,p ⋅ b₃ − … − X_p−2,p ⋅ b_p−2 − X_p−1,p ⋅ b_p−1

Then, express a_i in terms of b_i′s:

a₁ = b₁
a₂ = b₂ + X_1,2 ⋅ b₁
a₃ = b₃ + X_1,3 ⋅ b₁ + X_2,3 ⋅ b₂
a₄ = b₄ + X_1,4 ⋅ b₁ + X_2,4 ⋅ b₂ + X_3,4 ⋅ b₃
…
a_p = b_p + X_1,p ⋅ b₁ + X_2,p ⋅ b₂ + X_3,p ⋅ b₃ + … + X_p−2,p ⋅ b_p−2 + X_p−1,p ⋅ b_p−1

Further refine:

take X_i,i = 1, that is
a₁ = X_1,1 ⋅ b₁
a₂ = X_1,2 ⋅ b₁ + X_2,2 ⋅ b₂
a₃ = X_1,3 ⋅ b₁ + X_2,3 ⋅ b₂ + X_3,3 ⋅ b₃
a₄ = X_1,4 ⋅ b₁ + X_2,4 ⋅ b₂ + X_3,4 ⋅ b₃ + X_4,4 ⋅ b₄
…
a_p = X_1,p ⋅ b₁ + X_2,p ⋅ b₂ + X_3,p ⋅ b₃ + … + X_p−2,p ⋅ b_p−2 + X_p−1,p ⋅ b_p−1 + X_p,p ⋅ b_p

take X as an upper unit triangular matrix where Xi,i = 1 
X = 
X1,1 X1,2 X1,3 X1,4 .... X1,p  
 0    X2,2 X2,3 X2,4 .... X2,p
 0     0   X3,3 X3,4 .... X3,p
 0     0    0   X4,4 .... X4,p
   ..................
 0     0    0   0  ....   Xp,p

then,
A_m×p = [a₁|a₂|…|a_p], where a_i ∈ R^m,
B_m×p = [b₁|b₂|…|b_p], where b_i ∈ R^m,

take D = diag(||b₁||⁻¹, ||b₂||⁻¹, ||b₃||⁻¹,…,||b_p||⁻¹)
take Q = B ⋅ D = diag(b₁ ∕ ||b₁||, b₂ ∕ ||b₂||, b₃ ∕ ||b₃||,…, b_p ∕ ||b_p||)
take E = diag(||b₁||, ||b₂||, ||b₃||,…,||b_p||)…to eliminate D
take R = E ⋅ X = [(||b₁|| ⋅ X₁)|(||b₂|| ⋅ X₂)|(||b₃|| ⋅ X₃)|,…,|(||b_p|| ⋅ X_p)]…upper triangular matrix
then, A = B ⋅ X = B ⋅ D ⋅ E ⋅ X = Q ⋅ R …QR decomposition, where such Q ⋅ R is unique, ∵B ⋅ X is also unique, too.