Neural Network Basic Topology

19 Nov 2017

Neural Network Basic Topology

Neural network aims at non-linear hypothesis, binary and multiple classification. In the early 1990, it is believed that it achieves some training hypothesis and come out with results at certain convincible level. Due to the fact that it was not scaled very well to large problem at theat moment, it has been placed in the storage and it was almost the time I was a freshman in th euniversity. Due to H/W calculation and processing capability has a major improvement in the past two decads, in conjunction with big data science evolution due to open source environment, neural network has been re-inspected, even more, the deep learning has been build on top of its model representation. Although his founder Geoff Hilton suspects and claims that backward propagation might not be the most optimal approximation to the way human brain thinking, which is just like the case that jet engines could make human fly but human couldn't fly like a bird. With full understanding of its model, the way it supports training and recognition would be quiet an add-in in future involve in deep learning.

Model Representation By Intuition

Begin by a very basic realization that human receives external data from eyes, mouth, tongue, skin, then transfer to our brain, wherein, it is manipulated and classified to some other layers or groups of the neurons, which then take their turns to make further processing, maybe neuron transform in a recursive manner. The neural network is constructed with a hope to approximate the way our brain manipulating, training input and learning.

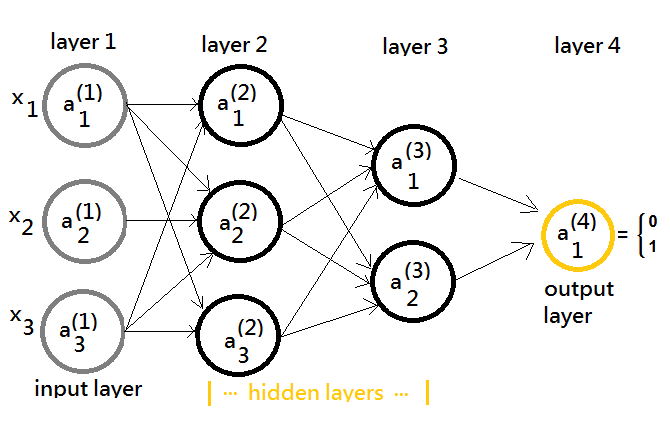
The model representation graph exhibits that there exists an input layer to receive the external data, an output layer to generate the outcome value, some hidden layes(in this example, layer 2, 3) in between the input and the output layer.
We can have the model more generalized in another graph.

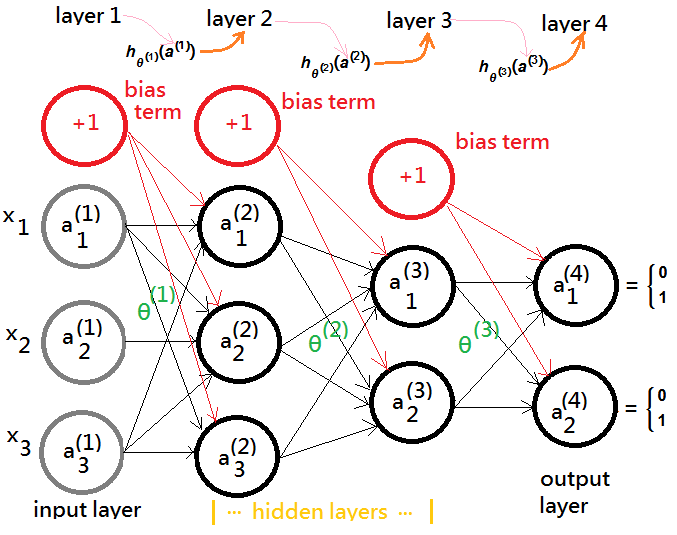
➀you can think of each distinct layer(except for the input layer) in the neural network the individual linear regression model, which (takes an intercept expressed by the bias term by statistics nature design). Specific cares for gradient descendent during backward propagation is mandatory, and the bias term is of no need for regularization!!
➁the $\theta^{(j)}$ is the weighting matrix, controlling the function mapping from layer $j$ to layer $j+1$.
➂the $a_i^{(j)}$ is used to denote the $i$-th activation function at layer $j$, wherein, it takes output from layer $j-1$ as its input and make advanced processing at its layer, output it, in turns becoming the input data to next layer $j+1$.
➃suppose we have the $a_1^{(1)}$, $a_2^{(1)}$,…, $a_n^{(1)}$ as the input data $x\in R^n$.
➄the output from layer $j$(the activation output at layer j) would be mapped to layer $j+1$ by $\theta^{(j)}$ as its input.
➅$h_{\theta^{(j)}}(a^{(j)})$ transforms $a^{(j)}$ with $\theta^{(j)}$ from layer $j$ to layer $j+1$ by means of logistic regression model.