Neural Network Feedforward Propagation

19 Nov 2017

Neural Network Feedforward Propagation

Neural network works as a whole to behave like a perceptron, the output from layer $j$ would be mapped by $\theta^{(j)}$ to the input of layer $j+1$. The final output in last layer would then be classified to the identity of the target object.

Neural Network Works by Feedforward Propagation

Recap the neural network model:

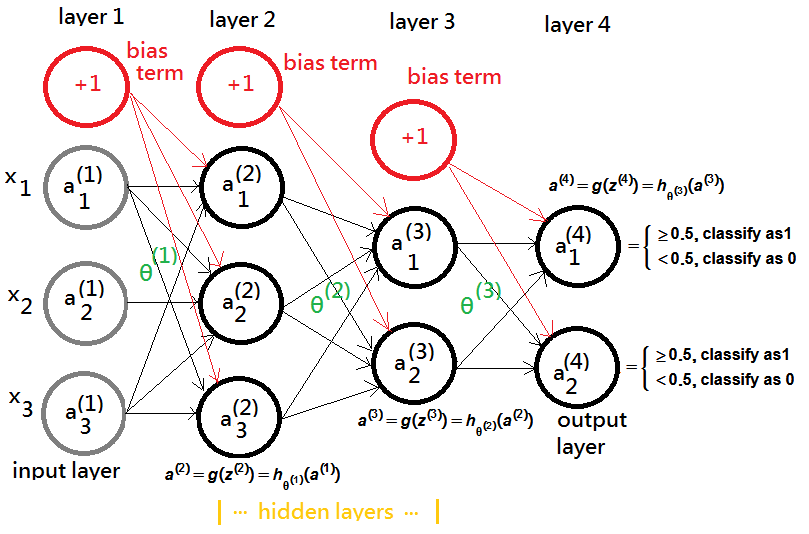
Note that for the ease of future backpropagation deduction, we further define below formula:
\(\begin{array}{l}a^{(j+1)}=g(z^{(j+1)})=h_{\mathrm\theta^{(\mathrm j)}}(a^{(\mathrm j)})\\,where\;z^{(j+1)}=(\theta^{(j)})^t\cdot a^{(j)},\;g(z)=\frac1{1+e^{-z}}\\\end{array}\)

You can treat g the sigmoid function taking the output($(\theta^{(j)})^t\cdot a^{(j)}$) from prior layer $j$, and transforms it to the input($a^{(j+1)}$) of next layer $j+1$ by means of the logistic regression.
➀from layer 1 to layer 2, we have:
\(\begin{array}{l}a^{(2)}=g(z^{(2)})=h_{\mathrm\theta^{(1)}}(a^{(1)})\\,where\;z^{(2)}=\theta^{(1)}\cdot a^{(1)}\\,a^{(1)}=x^{(i\_data)},1\leq i\_data\leq m\\\end{array}\)

➁from layer 2 to layer 3, we have:
\(\begin{array}{l}a^{(3)}=g(z^{(3)})=h_{\mathrm\theta^{(2)}}(a^{(2)}),where\;z^{(3)}=(\theta^{(2)})^t\cdot a^{(2)}\\\end{array}\)

➂from layer 3 to layer 4, we have:
\(\begin{array}{l}a^{(4)}=g(z^{(4)})=h_{\mathrm\theta^{(3)}}(a^{(3)}),where\;z^{(4)}=(\theta^{(3)})^t\cdot a^{(3)}\\\end{array}\)

➃at the last layer, in this example the layer 4 output, the final identity from logistic regression model would be determined at final layer:
\(\begin{array}{l}a^{(j+1)}=g(z^{(j+1)})=h_{\mathrm\theta^{(j)}}(a^{(j)})=\left\{\begin{array}{l}\geq0.5,clssify\;as\;1\\<0.5,classiy\;as\;0\end{array}\right.\\\end{array}\)