Neural Network Backward Propagation

20 Nov 2017

Neural Network Backward Propagation

Backward propagation is for the deduction of the $\theta_{i,j}^{(\mathcal l)}$ that could bring the error in the cost function to a minimum state. In neural network, gradient descendent is a mandatory mean to reach the $\theta_{i,j}^{(\mathcal l)}$ to the local minimum, and together with regularization to have an optimal approximation. Backward propagation proceeds in the reversed order and propagate the error from the final last one layer back to the the final last two layer, until the second layer, the algorithm would facilitate the whole gradient descendent process to find its local minimum.

The Regularized Neural Network Cost Function

The complete regularized cost function consists of two parts, part one is the cost function itself, part two is the regularized term:
\(\begin{array}{l}\underset{REG}{J(\theta)}=\frac1m\sum_{i=1}^m\sum_{k=1}^K\left[-y_k^{(i)}\cdot\log(h_\theta^{(k)}(x^{(i)}))-(1-y_k^{(i)})\cdot\log(1-h_\theta^{(k)}(x^{(i)}))\right]\\+\frac\lambda{2m}\sum_{\mathcal l=1}^{L-1}\sum_{j=1}^{j_\mathcal l}\sum_{k=1}^{k_\mathcal l}(\theta_{j,k}^{(\mathcal l)})^2\\,where\;h_\theta(x)\in R^K\\\end{array}\)

Suppose we are given totally m input data, the model where the cost function belongs to comes out with K outputs, and you all know that gradient descendent would be proceeded with derivation of $J(\theta)$ taken on the ($i,j$)th term in the weighting matrix $\theta^{(\mathcal l)}$ in between layer $\mathcal l$ and $\mathcal l+1$.

To make it more clear for the proof in next section, whenever you read $\theta_{i,j}^{(\mathcal l)}$, in this article, they are:
➀the weighting matrix $\theta^{(\mathcal l)}$ in between layer $\mathcal l$ and $\mathcal l+1$.
➁$i$ is the $i$-th row of the weighting matrix $\theta^{(\mathcal l)}$, it is also the $i$-th activation function in next layer $\mathcal l+1$.
➂{j} is the $j$-th output from the activation function at layer $\mathcal l$.
➃$\theta_{i,j}^{(\mathcal l)}$ translates the $j$-th output from the activation function at layer $\mathcal l$ into one of the input of the $i$-th activation function in next layer $\mathcal l+1$!!!!

All we need to compute are $J(\theta)$ and $\frac{\partial J(\theta)}{\partial\theta_{i,j}^{(\mathcal l)}}$ in a gradient descendent manner, the point is how to achieve the goal and why!

The Gradient Computation By Intuition

Take the cost function by intuition:
\(J(\theta)=-y^{(i\_data)}\cdot\log(h_\theta(x^{(i\_data)}))-(1-y^{(i\_data)})\cdot\log(1-h_\theta(x^{(i\_data)}))\) , where the $i$_$data$ is the index of the input data record.

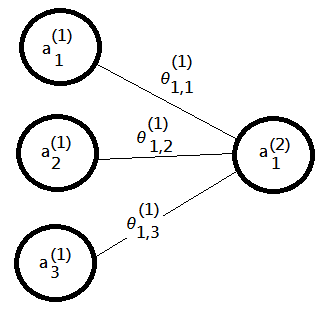
Suppose we are given $3\times1$ neural network model, we know:
➀$z_1^{(2)}=\theta_{1,1}^{(1)}\cdot a_1^{(1)}+\theta_{1,2}^{(1)}\cdot a_2^{(1)}+\theta_{1,3}^{(1)}\cdot a_3^{(1)}$
➁$a_1^{(2)}=g(z_1^{(2)})=\frac1{1+e^{-z_1^{(2)}}}$
➂take partial derivative of $J(\theta)$ on $\theta_{1,1}^{(1)}$, we would obtain:
\(\frac{\partial J(\theta)}{\partial\theta_{1,1}^{(1)}}=\frac{\partial J(\theta)}{\partial a_1^{(2)}}\cdot\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}\cdot\frac{\partial z_1^{(2)}}{\partial\theta_{1,1}^{(1)}}\)

This is the chain rule in calculus, which would mostly be applied in our later paragraph of proof.
But, why we have the term $\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}$?

Please be recalled that $a_1^{(2)}=g(z_1^{(2)})$

, where we have below deduction:
\(\begin{array}{l}\frac{\partial J(\theta)}{\partial a_1^{(2)}}=\frac{\partial(-y\cdot\log(a_1^{(2)})-(1-y)\cdot\log(1-a_1^{(2)}))}{\partial a_1^{(2)}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;=\frac{-y}{a_1^{(2)}}+\frac{1-y}{1-a_1^{(2)}}\cdots(a)\\\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}=\frac{\partial g(z_1^{(2)})}{\partial z_1^{(2)}}=g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdots(b)\\\frac{\partial z_1^{(2)}}{\partial\theta_{1,1}^{(1)}}=a_1^{(1)}\cdots(c)\end{array}\)

Then, combine above (a), (b), (c) terms, we can have:
\(\begin{array}{l}\frac{\partial J(\theta)}{\partial\theta_{1,1}^{(1)}}\\=(a)\cdot(b)\cdot(c)\\=\frac{-y\cdot(1-a_1^{(2)})+(1-y)\cdot a_1^{(2)}}{a_1^{(2)}\cdot(1-a_1^{(2)})}\cdot a_1^{(2)}\cdot(1-a_1^{(2)})\cdot a_1^{(1)}\\=(a_1^{(2)}-y)\cdot a_1^{(1)}\end{array}\)

Continue to apply, we can have results:
\(\left\{\begin{array}{l}\frac{\partial J(\theta)}{\partial\theta_{1,2}^{(1)}}=(a_1^{(2)}-y)\cdot a_2^{(1)}\\\frac{\partial J(\theta)}{\partial\theta_{1,3}^{(1)}}=(a_1^{(2)}-y)\cdot a_3^{(1)}\end{array}\right.\)

Next, we introduce $\delta_j^{(\mathcal l)}$, it is the error cost in $j$-th activation function of layer $\mathcal l$.
With above deduction result, for each distinct input data at index $i$_$data$, we can take error at output layer $2$(in this example):
\(\delta^{(2)}={\begin{bmatrix}\delta_1^{(2)}\end{bmatrix}}_{1\times1}=a_1^{(2)}-y^{(i\_data)}\)

Things would be a little complicated, before this article formularize the gradient computation for each $\frac{\partial J(\theta)}{\partial\theta_{i,j}^{(\mathcal l)}}$, just think that you can compute the errors from the final output layer, in the reversed order, back to the beginning second layer, and the output error from each layer $\mathcal l$ would then be propagated back into the gradient $\frac{\partial J(\theta)}{\partial\theta_{i,j}^{(\mathcal l-1)}}$.

Formularize The Gradient Computation - Mathematics Induction

From now on, we are going to do the real proof to formularize the gradient in neural network model:
[1]suppose you can recognize above proof given in $3\times1$ neural network model, and we have the finding: $$\frac{\partial J(\theta)}{\partial\theta_{i,j}^{(\mathcal l)}}=(a_i^{(\mathcal l+1)}-y^{(i\_data)})\cdot a_j^{(\mathcal l)}=\delta_i^{(\mathcal l+1)}\cdot a_j^{(\mathcal l)}$$

[2]next, we step further into 2 output nodes in final layer, $3\times2$ neural network model:

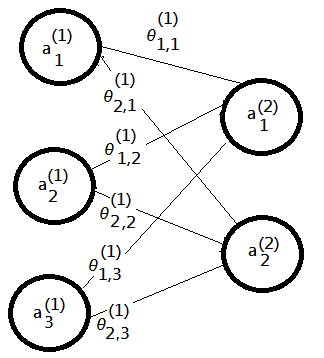
➀in this case, for $i=1,2$, we can have:
\(a_i^{(2)}=g(z_i^{(2)})=g(\theta_{i,1}^{(1)}\cdot a_1^{(1)}+\theta_{i,2}^{(1)}\cdot a_2^{(1)}+\theta_{i,3}^{(1)}\cdot a_3^{(1)})\)

➁succeeding to the result in [1];, take error costs at layer 2(in this example) as:
\(\delta_{2\times1}^{(2)}={\begin{bmatrix}\delta_1^{(2)}\\\delta_2^{(2)}\end{bmatrix}}_{2\times1}={\begin{bmatrix}a_1^{(2)}-y^{(i\_data)}\\a_2^{(2)}-y^{(i\_data)}\end{bmatrix}}_{2\times1}\)

➂we can deduce out:
\(\begin{array}{l}\frac{\partial J(\theta)}{\partial\theta_{1,1}^{(1)}}=\frac{\partial J(\theta)}{\partial a_1^{(2)}}\cdot\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}\cdot\frac{\partial z_1^{(2)}}{\partial\theta_{1,1}^{(1)}}\\=(a_1^{(2)}-y^{(i\_data)})\cdot a_1^{(1)}\end{array}\) \(\therefore\frac{\partial J(\theta)}{\partial\theta_{1,2}^{(1)}}=(a_1^{(2)}-y^{(i\_data)})\cdot a_2^{(1)}\) \(\therefore\frac{\partial J(\theta)}{\partial\theta_{1,3}^{(1)}}=(a_1^{(2)}-y^{(i\_data)})\cdot a_3^{(1)}\) \(\therefore\frac{\partial J(\theta)}{\partial\theta_{2,1}^{(1)}}=(a_2^{(2)}-y^{(i\_data)})\cdot a_1^{(1)}\) \(\therefore\frac{\partial J(\theta)}{\partial\theta_{2,2}^{(1)}}=(a_2^{(2)}-y^{(i\_data)})\cdot a_2^{(1)}\) \(\therefore\frac{\partial J(\theta)}{\partial\theta_{2,3}^{(1)}}=(a_2^{(2)}-y^{(i\_data)})\cdot a_3^{(1)}\)

By mathematics induction, we have a finding the same as the one in [1]: $$\frac{\partial J(\theta)}{\partial\theta_{i,j}^{(\mathcal l)}}=(a_i^{(\mathcal l+1)}-y^{(i\_data)})\cdot a_j^{(\mathcal l)}=\delta_i^{(\mathcal l+1)}\cdot a_j^{(\mathcal l)}$$

I have just proved for the simple model of only 2 layers, but, will the current finding hold for models of more than 3 layers?

[3]further step into $3\times2\times1$ neural network model:

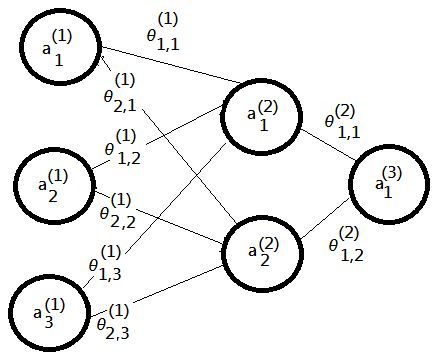
➀trivially, we can deduce out that:
\(\delta^{(3)}={\begin{bmatrix}\delta_1^{(3)}\end{bmatrix}}_{1\times1}={\begin{bmatrix}a_1^{(3)}-y^{(i\_data)}\end{bmatrix}}_{1\times1}\)

Then, we have a problem here, what is $\delta^{(2)}$? How to evaluate it? Since it is not at the final layer. What is the gradient descendent evaluation in $\theta^{(1)}$?

➁The same by taking partial derivative of $J(\theta)$:
\(\begin{array}{l}\frac{\partial J(\theta)}{\partial\theta_{1,1}^{(1)}}=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot\frac{\partial a_1^{(3)}}{\partial\theta_{1,1}^{(1)}}\\\end{array}\)
\(\begin{array}{l}=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot(\frac{\partial a_1^{(3)}}{\partial a_1^{(2)}}\cdot\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}\cdot\frac{\partial z_1^{(2)}}{\partial\theta_{1,1}^{(1)}}\\\end{array}\)
\(\begin{array}{l}+\frac{\partial a_1^{(3)}}{\partial a_2^{(2)}}\cdot\frac{\partial a_2^{(2)}}{\partial z_2^{(2)}}\cdot\frac{\partial z_2^{(2)}}{\partial\theta_{1,1}^{(1)}})\;\cdots\;\frac{\partial z_2^{(2)}}{\partial\theta_{1,1}^{(1)}}=0\\\end{array}\)
\(\begin{array}{l}=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot\frac{\partial z_1^{(3)}}{\partial a_1^{(2)}}\cdot\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}\cdot\frac{\partial z_1^{(2)}}{\partial\theta_{1,1}^{(1)}}\\\end{array}\)
\(\begin{array}{l}\cdots\frac{\partial a_1^{(3)}}{\partial a_1^{(2)}}=\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot\frac{\partial z_1^{(3)}}{\partial a_1^{(2)}}\\\end{array}\)
\(\begin{array}{l}=(a_1^{(3)}-y^{(i\_data)})\cdot\theta_{1,1}^{(2)}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdot a_1^{(1)}\\\end{array}\)
\(\therefore\frac{\partial J(\theta)}{\partial\theta_{1,2}^{(1)}}=(a_1^{(3)}-y^{(i\_data)})\cdot\theta_{1,1}^{(2)}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdot a_2^{(1)}\)
\(\therefore\frac{\partial J(\theta)}{\partial\theta_{1,3}^{(1)}}=(a_1^{(3)}-y^{(i\_data)})\cdot\theta_{1,1}^{(2)}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdot a_3^{(1)}\)
\(\therefore\frac{\partial J(\theta)}{\partial\theta_{2,1}^{(1)}}=(a_1^{(3)}-y^{(i\_data)})\cdot\theta_{1,2}^{(2)}\cdot g(z_2^{(2)})\cdot(1-g(z_2^{(2)}))\cdot a_1^{(1)}\)
\(\therefore\frac{\partial J(\theta)}{\partial\theta_{2,2}^{(1)}}=(a_1^{(3)}-y^{(i\_data)})\cdot\theta_{1,2}^{(2)}\cdot g(z_2^{(2)})\cdot(1-g(z_2^{(2)}))\cdot a_2^{(1)}\)
\(\therefore\frac{\partial J(\theta)}{\partial\theta_{2,3}^{(1)}}=(a_1^{(3)}-y^{(i\_data)})\cdot\theta_{1,2}^{(2)}\cdot g(z_2^{(2)})\cdot(1-g(z_2^{(2)}))\cdot a_3^{(1)}\)

➂we can normalize above result in this given example:
\(\frac{\partial J(\theta)}{\partial\theta_{i,j}^{(\mathcal l)}}=(a_1^{((\mathcal l+1)+1)}-y^{(i\_data)})\cdot\theta_{1,i}^{(\mathcal l+1)}\cdot g(z_i^{(\mathcal l+1)})\cdot(1-g(z_i^{(\mathcal l+1)}))\cdot a_j^{(\mathcal l)}\)
\(\therefore\delta_i^{(\mathcal l+1)}=(a_1^{((\mathcal l+1)+1)}-y^{(i\_data)})\cdot\theta_{1,i}^{(\mathcal l+1)}\cdot g(z_i^{(\mathcal l+1)})\cdot(1-g(z_i^{(\mathcal l+1)}))\)

➃For $\mathcal l=1$, we have error costs at layer two:
\(\delta_i^{(2)}=(a_1^{(3)}-y^{(i\_data)})\cdot\theta_{1,i}^{(2)}\cdot g(z_i^{(2)})\cdot(1-g(z_i^{(2)}))\)
where $i=1,2$, then:
\(\delta_{2\times1}^{(2)}={\begin{bmatrix}\delta_1^{(2)}\\\delta_2^{(2)}\end{bmatrix}}_{2\times1}\)
\(=(a_1^{(3)}-y^{(i\_data)})\cdot{\begin{bmatrix}\theta_{1,1}^{(2)}\\\theta_{1,2}^{(2)}\end{bmatrix}}_{2\times1}.\times\)
\({\begin{bmatrix}g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\\g(z_2^{(2)})\cdot(1-g(z_2^{(2)}))\end{bmatrix}}_{2\times1}\)
\(\cdots\;.\times\;element-wised\;operator\)
\(\cdots\begin{bmatrix}\theta^{(2)}\end{bmatrix}^t=\begin{bmatrix}\theta_1^{(2)}\\\theta_2^{(2)}\end{bmatrix}\)
\(=(a_1^{(3)}-y^{(i\_data)})\cdot{\begin{bmatrix}\theta_{1,1}^{(2)}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\\\theta_{1,2}^{(2)}\cdot g(z_2^{(2)})\cdot(1-g(z_2^{(2)}))\end{bmatrix}}_{2\times1}\)

By mathematics induction, we have a finding the same as the one in [1]: $$\frac{\partial J(\theta)}{\partial\theta_{i,j}^{(\mathcal l)}}=(a_i^{(\mathcal l+1)}-y^{(i\_data)})\cdot a_j^{(\mathcal l)}=\delta_i^{(\mathcal l+1)}\cdot a_j^{(\mathcal l)}$$

[4]further step into $3\times2\times2$ neural network model:

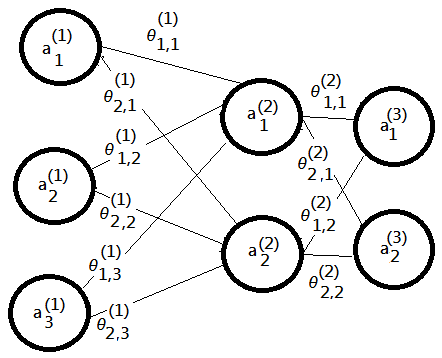
➀it would be easy to show error costs at layer three and two:
\(\delta_{2\times1}^{(3)}={\begin{bmatrix}\delta_1^{(3)}\\\delta_2^{(3)}\end{bmatrix}}_{2\times1}={\begin{bmatrix}a_1^{(3)}-y^{(i\_data)}\\a_2^{(3)}-y^{(i\_data)}\end{bmatrix}}_{2\times1}\)
\(\delta_{2\times1}^{(2)}=\begin{bmatrix}\theta^{(2)}\end{bmatrix}_{2\times2}^t\cdot{\begin{bmatrix}\delta^{(3)}\end{bmatrix}}_{2\times1}.\times{\begin{bmatrix}g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\\g(z_2^{(2)})\cdot(1-g(z_2^{(2)}))\end{bmatrix}}_{2\times1}\) \(\cdots\;.\times\;element-wised\;operator\)

➁first, evaluate $J(\theta)$ at layer 2, that is take derivation of $J(\theta)$ on $\theta_{i,j}^{(2)}$:
\(\begin{array}{l}\frac{\partial J(\theta)}{\partial\theta_{1,1}^{(2)}}=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot\frac{\partial a_1^{(3)}}{\partial\theta_{1,1}^{(2)}}\\=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot\frac{\partial z_1^{(3)}}{\partial\theta_{1,1}^{(2)}}\\=(a_1^{(3)}-y^{(i\_data)})\cdot a_1^{(2)}\\=\delta_1^{(3)}\cdot a_1^{(2)}\end{array}\)
\(\begin{array}{l}\therefore\frac{\partial J(\theta)}{\partial\theta_{1,2}^{(2)}}=\delta_1^{(3)}\cdot a_2^{(2)}\\\therefore\frac{\partial J(\theta)}{\partial\theta_{2,1}^{(2)}}=\delta_2^{(3)}\cdot a_1^{(2)}\\\therefore\frac{\partial J(\theta)}{\partial\theta_{2,2}^{(2)}}=\delta_2^{(3)}\cdot a_2^{(2)}\end{array}\)

➂we can by mathematics induction to have error costs at layer two:
\(\frac{\partial J(\theta)}{\partial\theta_{i,j}^2}=\delta_i^{(3)}\cdot a_j^{(2)}\)

➃next, evaluate $J(\theta)$ at layer 1, that is take derivation of $J(\theta)$ on $\theta_{i,j}^{(1)}$:
\(\begin{array}{l}\frac{\partial J(\theta)}{\partial\theta_{1,1}^{(1)}}=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot\frac{\partial a_1^{(3)}}{\partial\theta_{1,1}^{(1)}}+\frac{\partial J(\theta)}{\partial a_2^{(3)}}\cdot\frac{\partial a_2^{(3)}}{\partial\theta_{1,1}^{(1)}}\\=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot\frac{\partial z_1^{(3)}}{\partial\theta_{1,1}^{(1)}}\\+\frac{\partial J(\theta)}{\partial a_2^{(3)}}\cdot\frac{\partial g(z_2^{(3)})}{\partial z_2^{(3)}}\cdot\frac{\partial z_2^{(3)}}{\partial\theta_{1,1}^{(1)}}\end{array}\)
\(take\;part\;1=\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot\frac{\partial z_1^{(3)}}{\partial\theta_{1,1}^{(1)}}\)
\(take\;part\;2=\frac{\partial g(z_2^{(3)})}{\partial z_2^{(3)}}\cdot\frac{\partial z_2^{(3)}}{\partial\theta_{1,1}^{(1)}}\)

➄evaluate on $part\;1$:
\(part\;1=\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot(\frac{\partial z_1^{(3)}}{\partial a_1^{(2)}}\cdot\frac{\partial a_1^{(2)}}{\partial\theta_{1,1}^{(1)}}+\frac{\partial z_1^{(3)}}{\partial a_2^{(2)}}\cdot\frac{\partial a_2^{(2)}}{\partial\theta_{1,1}^{(1)}})\) \(=\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot(\theta_{1,1}^{(2)}\cdot\frac{\partial g(z_1^{(2)})}{\partial z_1^{(2)}}\cdot\frac{\partial z_1^{(2)}}{\partial\theta_{1,1}^{(1)}}+\)
\(\theta_{1,2}^{(2)}\cdot\frac{\partial g(z_2^{(2)})}{\partial z_2^{(2)}}\cdot\frac{\partial z_2^{(2)}}{\partial\theta_{1,1}^{(1)}})\cdots\frac{\partial z_2^{(2)}}{\partial\theta_{1,1}^{(1)}}=0\)
\(=\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot\theta_{1,1}^{(2)}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdot a_1^{(1)}\)

Then, evaluate on $part\;2$:
\(part\;2=\frac{\partial g(z_2^{(3)})}{\partial z_2^{(3)}}\cdot(\frac{\partial z_2^{(3)}}{\partial a_1^{(2)}}\cdot\frac{\partial a_1^{(2)}}{\partial\theta_{1,1}^{(1)}}+\frac{\partial z_2^{(3)}}{\partial a_2^{(2)}}\cdot\frac{\partial a_2^{(2)}}{\partial\theta_{1,1}^{(1)}})\)
\(\cdots\frac{\partial a_2^{(2)}}{\partial\theta_{1,1}^{(1)}}=0\)
\(=\frac{\partial g(z_2^{(3)})}{\partial z_2^{(3)}}\cdot\theta_{2,1}^{(2)}\cdot\frac{\partial{g(z_1^{(2)})}}{\partial z_1^{(2)}}\cdot\frac{\partial z_1^{(2)}}{\partial\theta_{1,1}^{(1)}}\)
\(=\frac{\partial g(z_2^{(3)})}{\partial z_2^{(3)}}\cdot\theta_{2,1}^{(2)}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdot a_1^{(1)}\)

➅back to the derivation of $J(\theta)$ on $\theta_{i,j}^{(1)}$, at this moment, take $part\;1$, $part\;2$ thus obtained in it:
\(\frac{\partial J(\theta)}{\partial\theta_{1,1}^{(1)}}=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot part\;1+\frac{\partial J(\theta)}{\partial a_2^{(3)}}\cdot part\;2\)
\(=\frac{\partial J(\theta)}{\partial a_1^{(3)}}\cdot\frac{\partial g(z_1^{(3)})}{\partial z_1^{(3)}}\cdot\theta_{1,1}^{(2)}\cdot g(z_1^{(2)})\cdot\)
\(\;\;\;\;\;\;\;\;(1-g(z_1^{(2)}))\cdot a_1^{(1)}\)
\(+\frac{\partial J(\theta)}{\partial a_2^{(3)}}\cdot\frac{\partial g(z_2^{(3)})}{\partial z_2^{(3)}}\cdot\theta_{2,1}^{(2)}\cdot g(z_1^{(2)})\cdot\)
\(\;\;\;\;\;\;\;\;(1-g(z_1^{(2)}))\cdot a_1^{(1)}\)
\(=\delta_1^{(3)}\cdot\theta_{1,1}^{(2)}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdot a_1^{(1)}\)
\(+\delta_2^{(3)}\cdot\theta_{2,1}^{(2)}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdot a_1^{(1)}\)
\(=\begin{bmatrix}\theta_{1,1}^{(2)}&\theta_{2,1}^{(2)}\end{bmatrix}\cdot\begin{bmatrix}\delta_1^{(3)}\\\delta_2^{(3)}\end{bmatrix}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\cdot a_1^{(1)}\)
\(=\delta_1^{(2)}\cdot a_1^{(1)}\)

➆next, we take $\delta_1^{(2)}$ to be $\begin{bmatrix}\theta_{1,1}^{(2)}&\theta_{2,1}^{(2)}\end{bmatrix}\cdot\begin{bmatrix}\delta_1^{(3)}\\delta_2^{(3)}\end{bmatrix}\cdot g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))$.
Therefore, we have $\frac{\partial J(\theta)}{\partial\theta_{1,2}^{(1)}}=\delta_1^{(2)}\cdot a_2^{(1)}$ and $\frac{\partial J(\theta)}{\partial\theta_{1,3}^{(1)}}=\delta_1^{(2)}\cdot a_3^{(1)}$

➇then, further deduce to have below:
\(\frac{\partial J(\theta)}{\partial\theta_{2,1}^{(1)}}=\begin{bmatrix}\theta_{1,2}^{(2)}&\theta_{2,2}^{(2)}\end{bmatrix}\cdot\begin{bmatrix}\delta_1^{(3)}\\\delta_2^{(3)}\end{bmatrix}\cdot\)
\(g(z_2^{(2)})\cdot(1-g(z_2^{(2)}))\cdot a_1^{(1)}\)
\(=\delta_2^{(2)}\cdot a_1^{(1)}\)
\(\therefore\frac{\partial J(\theta)}{\partial\theta_{2,2}^{(1)}}=\delta_2^{(2)}\cdot a_2^{(1)}\)
\(\therefore\frac{\partial J(\theta)}{\partial\theta_{2,3}^{(1)}}=\delta_2^{(2)}\cdot a_3^{(1)}\)
We found one thing that error costs also has similar scenario:
\(\delta_{2\times1}^{(2)}=\begin{bmatrix}\delta_1^{(2)}\\\delta_2^{(2)}\end{bmatrix}\)
\(=\begin{bmatrix}\theta^{(2)}\end{bmatrix}^t\cdot\delta^{(3)}.\times\begin{bmatrix}g(z_1^{(2)})\cdot(1-g(z_1^{(2)}))\\g(z_2^{(2)})\cdot(1-g(z_2^{(2)}))\end{bmatrix}\)

[5]By mathematics induction, we can claim for both the gradient and the error costs by below formula:

$$\frac{\partial J(\theta)}{\partial\theta_{i,j}^{(\mathcal l)}}=(a_i^{(\mathcal l+1)}-y^{(i\_data)})\cdot a_j^{(\mathcal l)}=\delta_i^{(\mathcal l+1)}\cdot a_j^{(\mathcal l)}$$ $$\delta^{(\mathcal l)}=\begin{bmatrix}\theta^{(\mathcal l)}\end{bmatrix}^t\cdot\delta^{(\mathcal l+1)}.\times\left[\begin{array}{c}g(z^{(\mathcal l)})\end{array}\cdot(1-g(z^{(\mathcal l)}))\right]$$

Cautions must be made that for bias term, $a_j^{(\mathcal l)}=1$, for $j=1$:
\(\frac{\partial J(\theta)}{\partial\theta_{1,1}^{(1)}}=\delta_1^{(2)}\cdot1\); \(\frac{\partial J(\theta)}{\partial\theta_{2,1}^{(1)}}=\delta_2^{(2)}\cdot1\),…

The Backward Propagation Algorithm

Supopose you are comfortable with erro cost in neural network model after deduction by mathemtics induction, this article would guide you through the backward propagation algorithm:
Given the training data set ${(x^{(1)},y^{(1)})\dots(x^{(m)},y^{(m)})}$
Initialize $\triangle_{i,j}^{(\mathcal l)}=0$ for all $i,j,\mathcal l$, below flow is in rather intuition. As to the coding detail, it would be in the impolementation section.