Prologue To Support Vector Machine

25 Nov 2017

Prologue To Support Vector Machine

Given training data set of size $n$, where they are {($x_1$, $y_1$), ($x_2$, $y_2$),...,($x_n$, $y_n$)}, $\forall x_i\in R^d$, $\forall y_i\in\{+1,-1\}$. Supposed these data could be classified and we'd like to learn a hyperplane classifier: $$f(x)=sign(w^t\cdot x-b)$$

Separating Hyperplane With Minimum Safe Guard

Furthermore, we want this hyperplane to have the minimum separating margin with respect to the two classes.

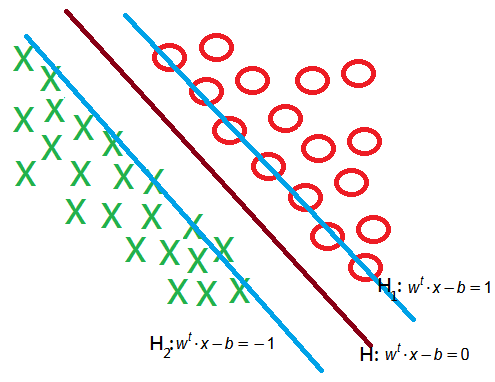
Specifically, if all goes well, there shall exist no data points in between $H_1$ and $H_2$.
\(\begin{array}{l}H:w^t\cdot x-b=0\\H_1:w^t\cdot x-b=1\\H_2:w^t\cdot x-b=-1\\\\\end{array}\)

For any separaing $H$ and the corresponding $H_1$ and $H_2$, we can solve by normalizing the coefficient vector $w$, such that $H_1$ and $H_2$ exist.
proof:
➀suppose $H_1:a^t\cdot x-b_1=0$ and $H_1:a^t\cdot x-b_2=0$ are two parallel hyperplanes. Since they are parallel, they can have the same weight $a$.
➁take $\overline b=\frac{b_1+b_2}2$ and $\delta=b_1-\overline b=\overline b-b_2$
\(\begin{array}{l}\therefore H_1:a^t\cdot x-(\delta+\overline b)=0\\\;\;\;\;H_2:a^t\cdot x-(\overline b-\delta)=0\\\therefore H_1:a^t\cdot x-\overline b=\delta\\\;\;\;\;H_2:a^t\cdot x-\overline b=-\delta\\\end{array}\)
➂then, divide both equality by $\delta$, we obtain:
\(\begin{array}{l}H_1:\frac{a^t}\delta\cdot x-\frac{\overline b}\delta=1\\H_2:\frac{a^t}\delta\cdot x-\frac{\overline b}\delta=-1\\\\\end{array}\)
➃take $w=\frac{a^t}\delta$ and $b=\frac{\overline b}\delta$, could we get our expected $H_1$ and $H_2$.

Next would be to maximize the distance between $H_1$ and $H_2$, therefore, there will be some positive examples on $H_1$, some negative examples on $H_2$.
These examples are called support vectors, only they participate in the separating hyperplane $H_1$ and $H_2$, other examples could be removed or moved around, since they didn’t cross $H_1$, $H_2$.

Distance Measurement Of Point To Line

Before step into support vector machine, have a galance at the measurement of distance from point to line.

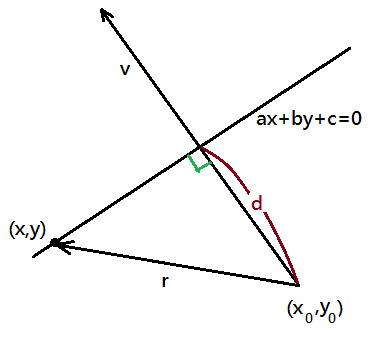
By given $a\cdot x+b\cdot y+c=0$ is a line parametric equation, then, $\frac ab\cdot x+y+\frac cb=0$; therefore, $y=-\frac ab\cdot x-\frac cb$ has slope $-\frac ab$.
➀pointers on this line could be expressed as below:
\(\begin{bmatrix}x\\-\frac ab\cdot x-\frac cb\end{bmatrix}=\begin{bmatrix}0\\-\frac cb\end{bmatrix}+(-\frac1b)\cdot\begin{bmatrix}-b\\a\end{bmatrix}\cdot x\)
➁therefore, \(\begin{bmatrix}-b\\a\end{bmatrix}\) is the vector parallel to this line, and \(\begin{bmatrix}a\\b\end{bmatrix}\) is the vector perpendicular to the line.
➂take $r=(x-x_0,y-y_0)$, by projecting $r$ onto $v$, then, we can deduce out $\left|Proj_v\cdot r\right|=\frac{\left|v^t\cdot r\right|}{\left|v\right|}$ to be the distance.
Since $v^t\cdot(r-v\cdot k)=0$, therefore, $k=\frac{v^t\cdot r}{v^t\cdot v}$,
\(\begin{array}{l}d=\left\|v\cdot\frac{v^t\cdot r}{v^t\cdot v}\right\|\\=\left\|\frac v{v^t\cdot v}\cdot v^t\cdot r\right\|\\=\left\|v\cdot(v^t\cdot v)^{-1}\cdot v^t\cdot r\right\|\\=\left\|(v^t)^{-1}\cdot v^t\cdot r\right\|\\=\frac{\left\|v^t\cdot r\right\|}{\left\|v^t\right\|}=\frac{\left\|v^t\cdot r\right\|}{\left\|v\right\|}\end{array}\)
➃suppose ($x$,$y$) is on $H$, by taking the absolute value of projecting $r$ onto $v$, we can get the distance from $H$ to $H_1$:
\(\begin{array}{l}\left|Proj_v\cdot r\right|\\=\frac{\left\|v^t\cdot r\right\|}{\left\|v\right\|},v=\left\langle a,b\right\rangle\\=\frac{\left|a\cdot(x-x_0)+b\cdot(y-y_0)\right|}{\sqrt{a^2+b^2}}\\=\frac{\left|a\cdot x+b\cdot y-(a\cdot x_0+b\cdot y_0)\right|}{\sqrt{a^2+b^2}}\\=\frac{\left|0-(-c)\right|}{\sqrt{a^2+b^2}}\\=\frac c{\sqrt{a^2+b^2}}\\=\frac{\left|a\cdot x_0+b\cdot y_0\right|}{\sqrt{a^2+b^2}}\end{array}\)