Markov Chain(Markov Process)
01 Dec 2017Markov Chain
A Glance At The Markov Chain
The Markov Chain consists of finite number of discrete states, probabilistic transition between states, maybe rewards of each state, and the most important is Markov Chain has no action control. No action to take, just from one state to another state.
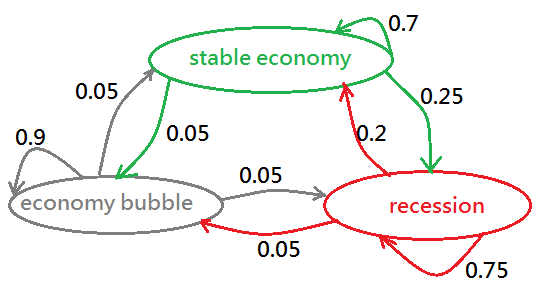
The 3 ellipses in different colors are individual states, where the green color indicates the stable state, the gray color stands for bubble state, the red color means the recession state. The transition probability is along each curve with its direction by the arrow. You can see that no any reward found in above graph, since the Markov Process don't always has the reward values associated with them.
Still another example of Markov Process is exhibited below, in this example, we add immediate reward on each state, R=0 for state 1, R=10 for state 2, R=0 for state 3:
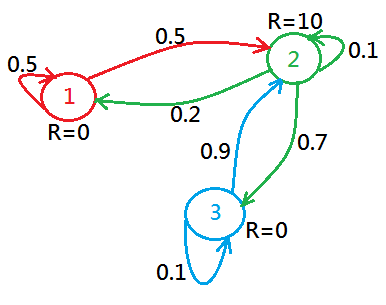
Notes that:
➀the probability on all the outgoing arcs of each state sum to one!
➁the Markov Process could be constructed with or without the reward in each state, it depends on artificial design.
➂no action to take, just transite from one state to another state.
The Markov Chain Components And Features
The primary components of the Markov Chain:
➀states
➁transition probabilities
➂rewardsThe major feature is that it has no actions to take, no decisions to make, just transits in between states.
The Markov Property
In Markov Process, next state is determined only by the current state, which is the Markov property.
Value Of A State
In this article, we express the value of a state over an infinite expected discounted horizon, and denote as V(S). That is to say we define the inifnite expected discounted reward as a function of the starting state. We’ll abbreviate V(S) as the value of a state. Here comes the question, how much total reward do we expect to get if we start in state S?
➀we will get an immediate reward R(S), just right in state S.
➁we will then get some reward in the future. The reward we get in the future is not worth as much to us as reward in the present, so we multiply by a discount factor gamma $\gamma$.
\(V(S)=R(S)+\gamma\cdot(?)\)
What The Future Might Be?
Given a intuition of value state, and a possible roadmap, what is the future value in the long run? The expected long term value of the next state is by summing over all possible next states, $S’$;where $S’$ is the product of:
➀the probability of making transition from $S$ to $S’$, $P(S'\left|S\right.)$.
➁the infinite horizon expected discounted reward(or the value of S’), $V(S')$.At this moment, take the future value of current state $S$ as immediate reward of current valus $S$ plus the expected long term value of the next state $S’$:
\(V(S)=R(S)+\gamma\cdot\sum_{S'}P(S'\left|S\right.)\cdot V(S')\)Suppose we know $R$ and $P$, next to compute $V$, if $n$ is the number of states in the domain, then, we have a set of $n$ equations in $n$ unknowns(the value of each state).
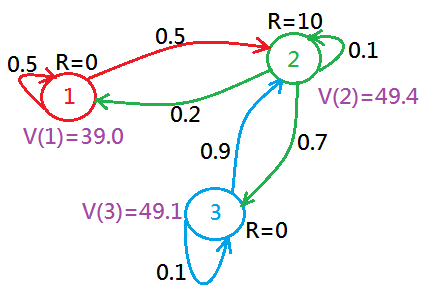
Continue with the three states example, given $\gamma=0.9$, by using above equation of intuition could we have future value illustration in below, whereas, in this example the initial value of each state is unknown:

If $\gamma=0$, then, the $V(S)$ of each state would just be the same as their immediate reward.
If $\gamma$ is small, but non-zero, then the value would be smaller.
Suppose after summing the next states $S’$ over a long horizon, we finally get it to the stable state with each state has its stable value.
What’s The Optimal Choice?
Here we are against a problem, if you are in one of the three states, what would be the optimal choice to get you the best next state? If such answer exists, it involves deterministics from within stochastic environment due to probabilistic state transition as a result of random action result. We’d like to further migrate into the field of Markov Decision Process, the computation requires extra deterministics.