Markov Decision Process By Intuition
01 Dec 2017Markov Decision Process By Intuition
From Markov Chain To Markov Decision Process
Back to have a glance at the Markov Chain, the future state value might be stablized. We wonder about the next state from current state, and would like to estimate it out. The estimation involves one extra consideration of action choice. The regularized solution would be a policy for each state to take its optimal action to maximize its value over horizon of some magnitude.
The Markov Decision Process Components And Features
➀a set of states, denote it as $S$.
➁a set of actions associated with states, denoted as $A$.
➂state transition probability, denote as $P(S_{t+1}\left|S_t\right.,a_t)$; where the Markov property claims:
\(P(S_{t+1}\left|S_t\right.,a_t)=P(S_{t+1}\left|S_t\right.,S_{t-1},\dots,S_0,a_t,a_{t-1},\dots,a_0)\)
That is to say given the current state and action, the next state is independent of the previous states and actions. The current state estimates all that is relevant about the world to predict what the next state will be.
➃immediate reward of each state, denoted as $R(S)$. Some article pertaining to MDP would treat it as the cost, which would also be used in our future illustration.The above four items are the major components in MDP. And from now on, we would use MDP in this article, even more, the whole dev blog, to stand for the Markov Decision Process.
MDP takes action in decision making process with a hope that it can regularize a policy for each state to have an optimal choice of action to maximize its expected state value estimated over herizon of magnitude of a long term, even infinity.
In advance to involve the policy, it would be better for us to distinguish in between conventional planning and MDP policy.
Conventional Plan v.s. MDP Policy
➀a plan is either an ordered list of actions or a partially ordered set of actions, executed without reference to the state of the environment.
➁for conditional planing, we treat it to act differently depending on the observation about the state of the world.
➂in MDP, it is typically to compute a whole policy rather than a simple plan.A policy is a mapping from states to actions, whatever state you happen to start from, a policy is the best to apply now.
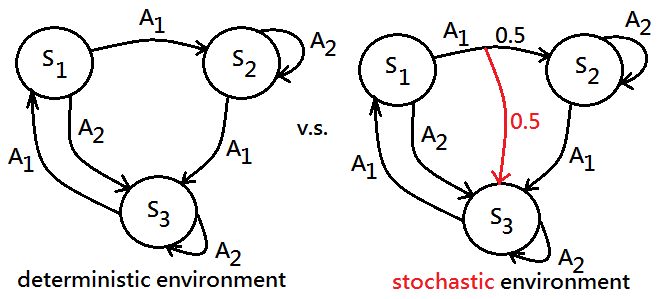
Stochastic v.s. Deterministic
You still ponder why to replace conventional planning with MDP policy, in this paragraph, we will further investigate in the differences in between stochastic and deterministic.
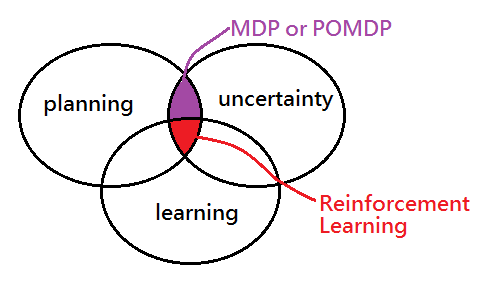
Below shows you an image of the appropriate discipline with respect to the desired behavior under the environment condition. For planning under uncertainty, we intend to refer to MDP or POMDP(PO means partial observable, would be discussed in another article), for learning, planning under under uncertainty, we will step into the reinforcement learning, still in another article.
Next to make a unique identity of stochastic and determninistic.
➀stochastic is an environment where the outcome of an action is somewhat random, that means, the execution result might not go as well as you have expected.
➁determninistic is an environment where the outcome of an action is predictable and always the same, that means the execution result would go as well as you have expected.

For the discipline of MDP, we are full observable under stochastic environment. Actually, full observable is impossible, we just believe that the design or hypothesis on the experimental environment is under the full control, but, anything out of the imagination would just errupt. More precisely, we should treat almost every issue under partial observable, and it would be the domain of POMDP(Partial Observable Markov Decision Process), discussed in another article in my dev blog. At this moment, focus on MDP only and hypnotize ourself that we have control everything.
At the end of this section, I would like to get you a clear expression of stochastic versus deterministic. Given below diagram of three states, with each state has two actions. The left side reveals the deterministic environment, each action is taken from each state to its next state, and the execution result is the same as expected; whereas the right side exhibits the stochastic environment, the execution of action $A_1$ from state $S_1$ has been branched into two results by random with each has $0.5$ chance to reach next state $S_2$ and $S_3$ respectively. This illustrates the result of action execution in stochastic environment is random.