Markov Decision Process In Stochastic Environment
03 Dec 2017Markov Decision Process In Stochastic Environment
Self Design Stochastic Environment
The most frequently used example is the information space build on the grid world. This article would just align with world’s grid world for MDP. Alternative illustration of other example would be found in later article in this dev blog.
Let’s begin by a design of 3 by 4 matrix of grid world, $M$. Take $M_{1,4}=+100$, $M_{2,4}=-100$ to be the terminal states with their value specified.
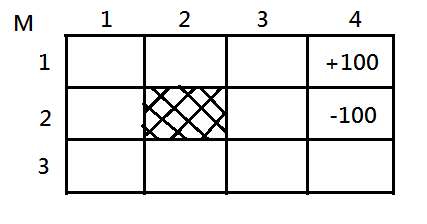
To make it into MDP, we assume actions are somewhar stochastic. Suppose we start from a grid cell and would like to head for the direction we intends to, the deterministic agent will always succeed to move in the direction it plans, on conditions that the target cell on that direction must be available.
But, the action execution result might not go as well as you have expected in the stochastic environment. By our design of stochastic environment, we assume that:
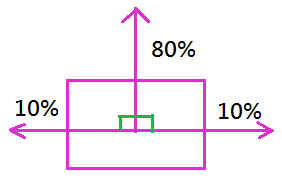
➀only $80\%$ chance for the stochastic agent to move in the direction it expects to.
➁if there is a wall blocking, then, it would bouncce back to the prior starting point, the same cell, with $80\%$ chance.
➂there is a $10\%$ chance to the direction left or right perpendicular to the expected direction, that’s say left or righ of $10\%$ chance respectively.Above design is just to make the outcome random, that is stochastic.
If the agent at $M_{3,3}$ would like to move to $M_{2,3}$, then, only $80\%$ chance to $M_{2,3}$, $10\%$ chance to $M_{3,2}$, $10\%$ chance to $M_{3,4}$.
If the agent at $M_{3,2}$ would like to move to $M_{2,2}$, then, $80\%$ chance to bounce back to $M_{3,2}$(since $M_{2,2}$ is a blocking wall), $10\%$ chance to $M_{3,1}$, $10\%$ chance to $M_{3,3}$.
Continue fo rthe illustration, if the agent at $M_{1,1}$ would like to move to north(its above), then, it will have totally $90\%$ chance to bounce back to $M_{1,1}$, wherein, $80\%$ chance bounce back from the north(above), $10\%$ chance bounce back from the left, and $10\%$ chance to $M_{1,2}$.
This is a stochastic state transition, so, if you planning a sequence of actions starting from $M_{3,1}$, to reach over the $+100$ at $M_{1,4}$, the final state, you might go N, N, E, E, E. But, with our design, the stochastic agent might move east with $10%$ chance to $M_{3,2}$.
So, we wish to have a planning method that provides an answer no matter where we are, that’s called a policy, where policy assigns actions to any state, that is:
$Poicy\;\pi(S)\rightarrow A$, for each state, we have to regularize a policy, the planning problem now becomes finding the optimal policy.
Conventional Planning In Stochastic Environment Is Insufficient
Suppose you are given the information space of the grid world, and would like to start from $M_{3,1}$ to reach the goal state at $M_{1,4}$. By the conventional planning, we might create a tree diagram to construct to possible state transition, since we are now in the stochastic environment, the outcome of action execution to 4 directions, north, south, west, east is not deterministic.
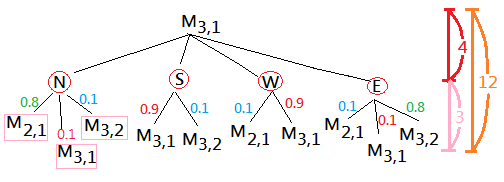
Departuring from $M_{3,1}$, you will have 4 possible action choices, they are N, S, W and E, by our design:
➀if you choose to go north, then, $80\%$ chance to $M_{2,1}$, $10\%$ chance to $M_{3,2}$, $10\%$ chance bounce back to $M_{3,1}$ due to the wall blocking.
➁if you choose to go south, then, $90\%$ chance bounce back to $M_{3,1}$ due to the wall blocking from south of $80\%$ chance and the west of $10\%$ chance, finally, $10\%$ chance to $M_{3,2}$.
➂if you choose to go west, then, $90\%$ chance bounce back to $M_{3,1}$ due to the wall blocking from south of $10\%$ chance and the west of $80\%$ chance, finally, $10\%$ chance to $M_{2,1}$.
➃if you choose to go east, then, $80\%$ chance to $M_{3,2}$, $10\%$ chance to $M_{2,1}$, $10\%$ chance bounce back to $M_{3,1}$.Take a good look at the tree diagram, the level 1 branching factor is 4, the second level is 3 by grouping the same arriving cell as one variety, then, total branching factor from $M_{3,1}$ would be less than and equal to 12. It would be a large value. If each movement is taken with the cost of 12 branching factors, and many of the next arriving cells has already been visited, conventional planning wouldn't be a good approach, and the whole tree would be too deep.
That's why we need to estimate out a policy to map each state to an optimal action to maximize the value of the state.
Stochastic Environment With Policy By Intuition
We are still using the same information space of the grid world, and the optimal action is the one that provides that you can run around as long as you want. So far, in this example, we are making the test under the assumption that each movement is taken at no cost, which is not the real thing in the real world!!
Consider by intuition the optimal action for you to start at below given distinct state(treat each cell to be one state) to end up in the $+100$ state at $M_{1,4}$:
➀begin from $M_{1,1}$, the most optimal step is to move to east of $80\%$ chance to be closed one direct step to $M_{1,4}$.
➁departure from $M_{3,1}$, it would be trivial to move to north, and $80\%$ chance to $M_{2,1}$.
➂kick off at $M_{3,4}$, it has $90\%$ chance to stay in the same place by moving south, since $80\%$ of bouncing back from the south wall, $10\%$ of bouncing back from the east wall. If you choose direct movement to west, then it would come out with $10\%$ danger of falling into the state of $-100$ at $M_{2,4}$. The same $90\%$ chance would get you in $M_{3,4}$, if you choose east movement, cautions must be made that moving to east would get you $10\%$ danger into the state of $-100$ at $M_{2,4}$. Hence, the optimal action is by moving south.
➃take a look at the case when you are beginning from $M_{2,3}$, moving north might not be optimal, you are running the danger of $10\%$ falling into the state of $-100$ at $M_{2,4}$, although, $80\%$ chance to the $M_{1,3}$. If you choose to move south, you still put yourself $10\%$ of the danger to the state of $-100$ at $M_{2,4}$. Why not just hitting the wall by moving west? Choose west movement would get you no any danger of falling to the state of $-100$ at $M_{2,4}$, although $80\%$ bounce back to $M_{2,3}$, you will have $10\%$ chance to the north at $M_{1,3}$ and $10\%$ chance to the south at $M_{3,3}$.
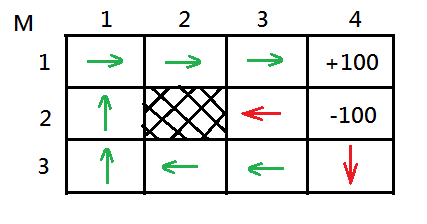
Above graph reveals the possible optimal action for all the states, quiet confusing about hitting wall(this would not be the general case in the real world), and it indeed bring you to the optimal next state. Take $M_{3,4}$ for example, maybe it would contiguous hitting the south wall in the beginning, then turns west sometime later, and behave like W, W, W, N, N, E, E, E to end up.