Markov Decision Process To Seek The Optimal Policy
04 Dec 2017Markov Decision Process To Seek The Optimal Policy
The Rewards(Costs)
If we are using the same grid world example, for the time being, we are really ignoring the issue of costs, or some articles prefer to use the term rewards. The two are the same meaning in MDP. In the real world, the moving to other location costs, like fuel, power consumption, time spends, these might be the unwanted burden, but inevitable.
Then, what is reward we are speaking of? For example, you will get 1000$ upon winning the championship in the swimming competition, that’s the reward. Still another example, if you are struggle to the river, by making one movement nearby to the riverside, just by leaving current far distance position, your spiritual would be encouraged, such encouragement would be the reward.
In MDP, usually, by design, when you would like to step into another state, upon leaving current state, you would be rewarded with a quantitative value. For the cost, it is explicitly a negative reward per state. As to the reward, it might be a positive value.
Policy Over Infinite Horizon
The criteria for finding a good policy is to find the policy that for each state, the expected reward of executing that policy is maximized, starting from that state. For each state, find the single action that maximizes the expected rewards.
In many cases, it is not very clear how long the process is going to run, it is often popular to move toward optimality with a discount factor gamma $\gamma$. The objective is to find a policy $\pi:S\rightarrow A$ that can maximize the given expression:
\(E\left[\sum_{t=0}^\infty\gamma^t\cdot R_t\left|S_0\right.\right]\)It is just the expression of the expected sum of future possible discounted rewards, where $0\leq\gamma\leq1$. And why $\gamma$ is introduced(we already touch gamma in the article of Markov Chain)?
➀if we add up all rewards out into infinity, then, sums might be infinite, but, this is not the ordinary case.
➁by such design, a discount factor $\gamma$ could speed up the agent to get rewards sooner rather than later.
➂the $\gamma$ decays the future rewards; it is a kind of alternative to specify the costs(rewards).So, we are ready to state the actual objective of an MDP is to minimize not just the momentary cost(or maximize the momentary reward, in other words), but the sum of future rewards would be the optimized target!!
The Optimal Value Function
Succeeding to the expression of the expected sum of future possible discounted rewards, to get the optimal policy, we need to further refine the state value function so that it would be optimal for computation of policy:
\(V^\pi(S)=\underset\pi E\left[\sum_{t=0}^\infty\gamma^t\cdot R\left|S_0\right.=S\right]\)For each state $S$, the value function of the state is the expected sum of future discounted reward, provided that you execute the policy $\pi$.
The way we are going to plan is that we are going to iterate and compute value function of each state, then, it will turn out for us to have a better policy. This process is usually discounted by $\gamma$, and we also add the reward or the cost of the starting state.
Because there are multiple actions associated with each distinct state, it’s your choice to select the right action that will maximize over all possible actions, this is an equation called backup:
\(V(S)\leftarrow R(S)+\underset A{max}\left[\gamma\cdot\sum_{S'}P(S'\left|S,A\right.)\cdot V(S')\right]\)The reason you see this left arrow in above expression is due to we are using a recursive algorithm to calculate the value function of each state. By the introduction of discount factor gamma $\gamma$, after iteration over some horizon, the Calculus just guarantees the convergence of the value function. At that moment, we can just have below optimal value function:
\(V(S)=R(S)+\underset A{max}\left[\gamma\cdot\sum_{S'}P(S'\left|S,A\right.)\cdot V(S')\right]\)You can see that it is now the equal operator in the expression. Just at this moment, we can know the optimal action from the optimal policy of each state with regards to its optimal value function. When the equation holds true, we have what is called a Bellman equality or Bellman equation.
The Bellman equation contains 2 parts:
➀$R(S)$, the reward(cost) in the state $S$.
➁$\underset A{max}\left[\gamma\cdot\sum_{S’}P(S’\left|S,A\right.)\cdot V(S’)\right]$, the maximum over all actions we could take in the state $S$, of the discounted expected optimal value of next state $S’$.
Value Iteration Under Stochastic Environment Of The Grid World
The idea behind is that in every state, we want to choose the action that maximize the value of the future. This paragraph would lead you through the whole process still in example of the grid world.
The stochastic environment of grid world with the same setting and the action has the stochastic outcomes, where $80\%$ is the probability we can get our action of our command done, otherwise, we get left or right.
At this time, we are not forgetting the issue of costs, we denote costs as the award function over all possible states, below design might be an incentive to shorten the action sequence, the agent should complete as soon as possible, or the value function of each iterated state might be decreased:
\(R(S)=\left\{\begin{array}{c}+100,for\;M_{1,4}\\-100,for\;M_{2,4}\\-3,othewise\end{array}\right.\)Assume that the initial values are all $0$, except for $M_{1,4}=+100$, $M_{2,4}=-100$ and $\gamma=1$ for simplicity.
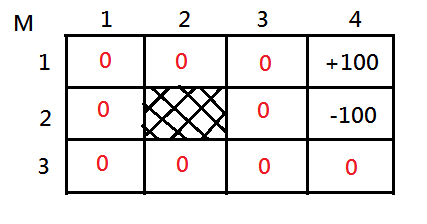
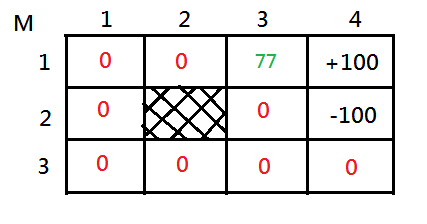
[1]Let’s try to calculate the value of $M_{1,3}$ after a single backup.
➀$V(M_{1,3},E)=-3+0.8\cdot100+0.1\cdot0+0.1\cdot0=77$, for we choose east, the immediate reward of leaving $M_{1,3}$ is $-3$, and $80\%$ chance to arrive $M_{1,4}$ of reward $+100$, $10\%$ chance to bounce back to $M_{1,3}$ of reward $0$, $10\%$ chance to down to $M_{2,3}$ of reward $0$.
➁$V(M_{1,3},W)=-3+0.8\cdot0+0.1\cdot0+0.1\cdot0=-3$, for we choose west, the immediate reward of leaving $M_{1,3}$ is $-3$, and $80\%$ chance to arrive $M_{1,2}$ of reward $0$, $10\%$ chance to bounce back to $M_{1,3}$ of reward $0$, $10\%$ chance to down to $M_{2,3}$ of reward $0$.
➂$V(M_{1,3},N)=-3+0.8\cdot0+0.1\cdot0+0.1\cdot100=7$, for we choose north, the immediate reward of leaving $M_{1,3}$ is $-3$, and $80\%$ chance to bounce back to $M_{1,3}$ of reward $0$, $10\%$ chance to $M_{1,2}$ of reward $0$, $10\%$ chance to $M_{1,4}$ of reward $100$.
➃$V(M_{1,3},S)=-3+0.8\cdot0+0.1\cdot0+0.1\cdot100=7$, for we choose south, the immediate reward of leaving $M_{1,3}$ is $-3$, and $80\%$ go to $M_{2,3}$ of reward $0$, $10\%$ chance to $M_{1,2}$ of reward $0$, $10\%$ chance to $M_{1,4}$ of reward $100$.
Trivially, we have $V(M_{1,3},E)=77$ the maximized value, and the east is the optimal action.
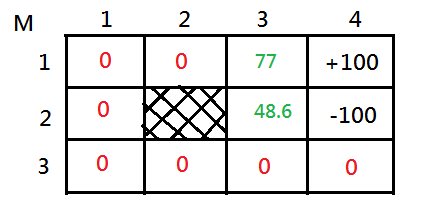
[2]Suppose we are inheriting from above state, where $V(M_{1,3})=77$, what is the value of $M_{2,3}$ after still another single backup?
➀$V(M_{2,3},E)=-3+0.8\cdot-100+0.1\cdot77+0.1\cdot0=-75.3$, for we choose east, the immediate reward of leaving $M_{2,3}$ is $-3$, and $80\%$ chance to arrive $M_{2,4}$ of reward $-100$, $10\%$ chance to $M_{1,3}$ of reward $77$, $10\%$ chance to down to $M_{3,3}$ of reward $0$.
➁$V(M_{2,3},W)=-3+0.8\cdot0+0.1\cdot77+0.1\cdot0=4.7$, for we choose west, the immediate reward of leaving $M_{2,3}$ is $-3$, and $80\%$ chance to bounce back to $M_{2,3}$ of reward $0$, $10\%$ chance to $M_{1,3}$ of reward $77$, $10\%$ chance to down to $M_{3,3}$ of reward $0$.
➂$V(M_{2,3},N)=-3+0.8\cdot77+0.1\cdot0+0.1\cdot-100=48.6$, for we choose north, the immediate reward of leaving $M_{2,3}$ is $-3$, and $80\%$ chance to arrive $M_{1,3}$ of reward $77$, $10\%$ chance to bounce back to $M_{2,3}$ of reward $0$, $10\%$ chance to down to $M_{2,4}$ of reward $-100$.
➃$V(M_{2,3},S)=-3+0.8\cdot0+0.1\cdot0+0.1\cdot-100=-13$, for we choose south, the immediate reward of leaving $M_{2,3}$ is $-3$, and $80\%$ chance to arrive $M_{3,3}$ of reward $0$, $10\%$ chance to bounce back to $M_{2,3}$ of reward $0$, $10\%$ chance to down to $M_{2,4}$ of reward $-100$.
Trivially, we have $V(M_{2,3},N)=48.6$ the maximized value, and the north is the optimal action. Please be recalled that hitting the wall is not the most optimal action any more, it is a major different from prior illustration! That's because we have successfully backup a optimal value of $M_{1,3}=77$.
We can propagate value backwards in reverse order of action, executing from $M_{1,4}=+100$, through this grid world and fill every every single state with a better value estimation. If we do this, run the value iteration through convergence, then, we get the following value function:
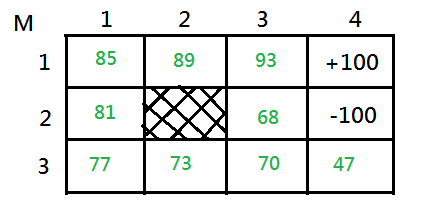
Below is the corresponding mapping of optimal policy containing an optimal action to each distinct state that can maximize its future value function:
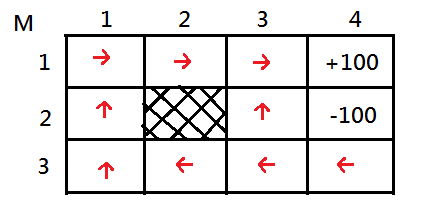
After following up above iteration, you might be impressed with such backup process by propagating value function in reverse order sequence of action executing from the goal state back to its previous state.
Value Iteration Under Stochastic Environment Of Two States World
Next, I am going to illustrate in a more general case of stochastic environment containing only 2 states. That’s for the better understanding and ease of computation. In this example, the goal state would be the estimated out target.
Suppose you are given below 2 states environment with each initialized with value function $0$, the red curve is the action you try to stay in the same state, that says you try to stop, while the blue curve is the action to move to another state:
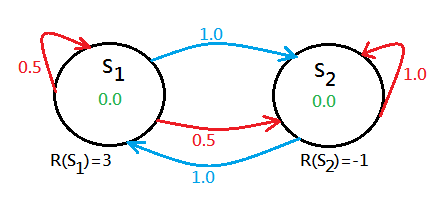
➀the $S_1$ has both stop and move actions, the stop execution will have $50\%$ chance to stay, $50\%$ chance to move to $S_2$, the move action will have $100\%$ chance to reach $S_2$.
➁the $S_2$ has both stop and move actions, the stop execution will have $100\%$ chance to stay, the move action will have $100\%$ chance to reach $S_1$.
➂the immediate rewards are $R(S_1)=3$ and $R(S_2)=-1$.
Where the move action always succeeding in switching in between the 2 states, the stop action fully works only when it reaches the bad state, $R(S)=-1$. Given $\gamma=0.5$ for a little tricky.Here is an extra rule, when you apply value iteration, it is in the unit of the whole stochastic environment, not only in some fixed order of state. That is to say the whole system of 2 states would be updated with new value function simultaneously, and then you can start again with the new value functions in the 2 states.
[1]Let’s calculate the value function of $S_1$, beginning over here:
➀$V(S_1,stop)=3+0.5\cdot(0.5\cdot0+0.5\cdot0)=3$, the stop action would come out with $50\%$ chance staying in the same place of reward $0$, $50\%$ chance to the $S_2$ of reward $0$.
➁$V(S_1,move)=3+0.5\cdot(1.0\cdot0)=3$, the move action would come out with $100\%$ chance to the $S_2$ of reward $0$.
Trivially, $V(S_1)=3$, the optimal action of $S_1$ could not be tell at this moment, then, figure out the value function of $S_2$:
➂$V(S_2,stop)=-1+0.5\cdot(1.0\cdot0)=-1$, the stop action would come out with $100\%$ chance to stay in $S_2$ of reward $0$.
➃$V(S_2,move)=-1+0.5\cdot(1.0\cdot0)=-1$, the move action would come out with $100\%$ chance to the $S_1$ of reward $0$.
Trivially, $V(S_2)=-1$, the optimal action of $S_2$ could not be tell at this moment, either.
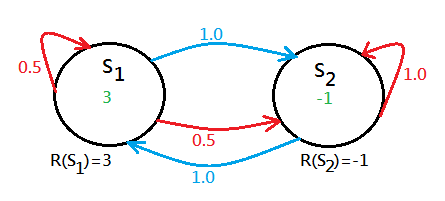
[2]The current optimal value functions are $V(S_1)=3$ and $V(S_2)=-1$, continue to do the value iteration again:
➀$V(S_1,stop)=3+0.5\cdot(0.5\cdot3+0.5\cdot-1)=3.5$, the stop action would come out with $50\%$ chance staying in the same place of reward $3$, $50\%$ chance to the $S_2$ of reward $-1$.
➁$V(S_1,move)=3+0.5\cdot(1.0\cdot-1)=2.5$, the move action would come out with $100\%$ chance to the $S_2$ of reward $-1$.
Trivially, $V(S_1)=3.5$, the optimal action of $S_1$ could be stop at this moment, then, figure out the value function of $S_2$:
➂$V(S_2,stop)=-1+0.5\cdot(1.0\cdot-1)=-1.5$, the stop action would come out with $100\%$ chance to stay in $S_2$ of reward $-1$.
➃$V(S_2,move)=-1+0.5\cdot(1.0\cdot3)=0.5$, the move action would come out with $100\%$ chance to the $S_1$ of reward $3$.
Trivially, $V(S_2)=0.5$, the optimal action of $S_2$ could be regarded as move at this moment.
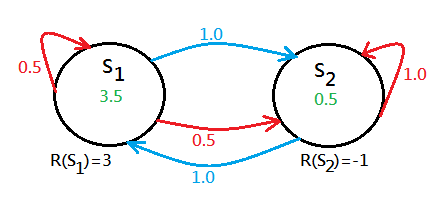
Keep on applying value iteration onto the whole system, we will finally bring the value function of the 2 states to the convergence.
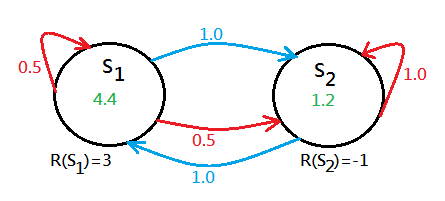
➀$V(S_1,stop)=3+0.5\cdot(0.5\cdot4.4+0.5\cdot1.2)=4.4$, the stop action would come out with $50\%$ chance staying in the same place of reward $4.4$, $50\%$ chance to the $S_2$ of reward $1.2$.
➁$V(S_1,move)=3+0.5\cdot(1.0\cdot1.2)=3.6$, the move action would come out with $100\%$ chance to the $S_2$ of reward $1.2$.
Trivially, $V(S_1)=4.4$, the optimal action of $S_1$ could be stop at this moment, then, figure out the value function of $S_2$:
➂$V(S_2,stop)=-1+0.5\cdot(1.0\cdot1.2)=-0.4$, the stop action would come out with $100\%$ chance to stay in $S_2$ of reward $1.2$.
➃$V(S_2,move)=-1+0.5\cdot(1.0\cdot4.4)=1.2$, the move action would come out with $100\%$ chance to the $S_1$ of reward $4.4$.
Trivially, $V(S_2)=1.2$, the optimal action of $S_2$ could be regarded as move at this moment.If you treat $S_1$ as sprinting, $S_2$ as jogging, then you will found the most optimal policy for you is to keep on sprinting!! Could we regard it as sprinting costs much fat than jogging, so, everyone should sprint, not jog?
The Optimal Policy Given The Optimal Value Function
At the end of this article, I’d like to generalize the optimal policy. Suppose you have a full understanding of above value iteration process, then, we generalize the optimal policy below:
\(\pi(S)=\underset A{armax}\sum_{S'}P(S'\left|S,A\right.)\cdot V(S')\)
where $\pi(S)$ is the policy $\pi$ for the state $S$, it would yield out the action $A$ that maximizes the value function of a state $S$. The $\gamma$ and the immediate reward has been tossed out, with or without them, th eresult wouldn’t change.