Introduction To The Chi-Square Distribution

03 Jan 2018

Prologue To The Chi-Square Distribution

In probability theory and statistics, base on the most fundamental gamma distribution, one of the many models of distributions further developed is the chi-square distribution. With the basic realization of gamma distribution, we can treat the chi-square distribution a special case of the gamma distribution. It would be greatly helpful in the evaluation of the regression model build on your hypothesis, the power of test for the precision in the machine learning results.

From The Gamma Distribution To The Chi-Square Distribution

Be recalled that we have gamma function and the PDF of the gamma distribution:
➀$\Gamma(\alpha)$=$\int_0^\infty x^{\alpha-1}\cdot e^{-x}\operatorname dx$, where $\alpha>0$.
➁$f(x)=\frac {1}{\beta^{\alpha}\cdot\Gamma(\alpha)}\cdot x^{\alpha-1}\cdot e^{-\frac{x}{\beta}}$, where $\alpha>0$, $\beta>0$

Next, we take $\alpha=\frac\nu2$, $\beta=2$, we turn the PDF function into below expression:
$f(x)=\frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot x^{\frac \nu2 -1}\cdot e^{-\frac {x}{2}}$, for $x>0$
, where $\nu$ is a positive integer, and this is the chi-square PDF.

It is just a special case of the gamma distribution with $\alpha=\frac\nu2$, $\beta=2$, and $\nu$ is the degree of freedom.

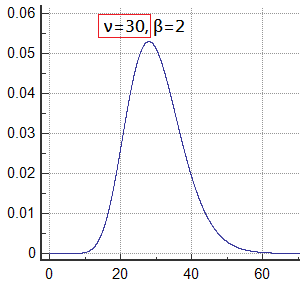
The Chi-Square Distribution Is Right-Skew

As degree of freedom increases, chi-square distribution would approximate the normal distribution.

You can easily see that as $\nu$ increases, the distribution of chi-square changes.
Gradually, it will approximate the normal distribution.

The Chi-Square And The MGF, Why?

Because by means of the moment, we can easily figure out the $E\lbrack X\rbrack$, $E\lbrack X^2\rbrack$, $E\lbrack X^3\rbrack$ with 1st, 2nd, 3rd order of differentiation.
➀we can formulate the MGF of chi-square in below expression:
$M_X(t)=\int_0^\infty e^{t\cdot x}\cdot \frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot x^{\frac \nu2 -1}\cdot e^{-\frac {x}{2}}\operatorname dx$
$\;\;\;\;\;\;=\int_0^\infty \frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot x^{\frac \nu2 -1}\cdot e^{-\frac {1}{2}\cdot (1-2\cdot t)\cdot x}\operatorname dx$

➁let $y=\frac {1}{2}\cdot (1-2\cdot t)\cdot x$
$\Rightarrow x=\frac {2\cdot y}{1-2\cdot t}$
$\Rightarrow \frac {\operatorname dx}{\operatorname dx}=\frac {2}{1-2\cdot t}\cdot\frac {\operatorname dy}{\operatorname dx}$
$\Rightarrow 1\cdot \operatorname dx=\frac {2}{1-2\cdot t}\cdot \operatorname dy$
$\Rightarrow \operatorname dx=\frac {2}{1-2\cdot t}\cdot \operatorname dy$

➂replace $\operatorname dx$ with $\frac {2}{1-2\cdot t}\cdot \operatorname dy$
$M_X(t)=\int_0^\infty \frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot (\frac {2\cdot y}{1-2\cdot t})^{\frac \nu2 -1}\cdot e^{-y}\cdot\frac {2}{1-2\cdot t}\cdot \operatorname dy$
$\;\;\;\;\;\;=\frac {1}{2^{\frac \nu2}\cdot\Gamma(\frac \nu2)}\cdot (\frac {2}{1-2\cdot t})^{\frac \nu2}\cdot\int_0^\infty y^{\frac \nu2 -1}\cdot e^{-y} \operatorname dy$
$\;\;\;\;\;\;=\frac {1}{2^{\frac \nu2}\cdot\Gamma(\frac \nu2)}\cdot (\frac {2}{1-2\cdot t})^{\frac \nu2}\cdot\Gamma(\frac \nu2)$
$\;\;\;\;\;\;=(\frac {1}{1-2\cdot t})^{\frac \nu2}$
$\;\;\;\;\;\;=(1-2\cdot t)^{-\frac \nu2}$
, where we have $\Gamma(\frac \nu2)$=$\int_0^\infty y^{\frac \nu2 -1}\cdot e^{-y} \operatorname dy$

Expect Value And Variance Of Chi-Square Distribution

Succeeding to above, we have deduce out the MGF of chi-square, we could just easily figure out the $\mu_1$, $\mu_2$:
$\mu_1$=$M_X^{′}(t)\vert_{t=0}$
$\;\;\;\;$=$\frac{\operatorname dM_X(t)}{\operatorname dt}\vert_{t=0}$
$\;\;\;\;$=$-\frac {\nu}{2}\cdot (1-2\cdot t)^{-\frac \nu2 -1}\cdot (-2)\vert_{t=0}$
$\;\;\;\;$=$\nu\cdot (1-2\cdot t)^{-\frac \nu2 -1}\vert_{t=0}$
$\;\;\;\;$=$\nu$=$E\lbrack X\rbrack$

$\mu_2$=$M_X^{″}(t)\vert_{t=0}$
$\;\;\;\;$=$\frac{\operatorname d^{2}M_X(t)}{\operatorname dt^{2}}\vert_{t=0}$
$\;\;\;\;$=$\nu\cdot (-\frac {\nu}{2}-1)\cdot (1-2\cdot t)^{-\frac \nu2 -2}\cdot (-2)\vert_{t=0}$
$\;\;\;\;$=$2\cdot\nu\cdot (\frac {\nu}{2}+1)\cdot (1-2\cdot t)^{-\frac \nu2 -2}\vert_{t=0}$
$\;\;\;\;$=$\nu^2+2\cdot\nu$=$E\lbrack X^2\rbrack$

Therefore, $Var\lbrack X\rbrack$=$E\lbrack X^2\rbrack-E^2\lbrack X\rbrack$=$2\cdot\nu$

$Z^2\sim\chi_1^2$

In this section, I’d like to prove that $Z^2\sim\chi_1^2$, it says that the squared standard normal distribution is similar or even approximate to the chi-square distribution.

Well, we denote $ɸ(0,1)$ to be the standard normal distribution with mean $0$ and variance $1$, and $\chi_i^2$ to stand for the chi-square distribution, with degree of freedom equal to $i$. If you see $\chi_1^2$, it means ch-square with degree of freedom $1$.

proof:
➀we’ll use Jacobian for the change of variable in this proof.
Given $x\in X$, $y\in Y$, $X$ and $Y$ are two random variables.
Suppose $f_X(x)$ is the PDF of $X$, and $f_Y(y)$ is the PDF of $Y$, then, below equality just holds.
$\int_0^\infty f_Y(y) \operatorname dy$=$1$=$\int_0^\infty f_X(x) \operatorname dx$
$\Rightarrow\frac {\operatorname d\int_0^\infty f_Y(y) \operatorname dy}{\operatorname dy}$=$\frac {\operatorname d\int_0^\infty f_X(x) \operatorname dx}{\operatorname dy}$
$\Rightarrow f_Y(y)$=$\frac {f_X(x)\operatorname dx}{\operatorname dy}$
$\Rightarrow f_Y(y)$=$f_X(x)\cdot\frac {\operatorname dx}{\operatorname dy}$
where we denote $J=\frac {\operatorname dx}{\operatorname dy}$

➁suppose the random variable $X$ is normal distributed with $\mu$ as its mean, and $\sigma^2$ as its variance, where we denote it $X\sim N(\mu,\sigma^2)$.

Suppose $Z$ is another random variable. If for all $z\in Z$, we take $z$=$\frac {x-\mu}{\sigma}$, then, $Z\sim ɸ(0,1)$ and below PDF of $Z$ just holds.
$f_Z(z)$=$\frac {1}{\sqrt{2\cdot\pi}}\cdot e^{-\frac{z^2}{2}}$

➂for all $y\in Y$, $z\in Z$, let $Y=Z^2$, then, $Z=\pm\sqrt Y$,
Further take $Z_1=-\sqrt Y$, $Z_2=\sqrt Y$, therefore, we have:
$\frac {\operatorname dz_1}{\operatorname dy}$=$-\frac {1}{2\cdot\sqrt y}$=$J_1$
$\frac {\operatorname dz_2}{\operatorname dy}$=$\frac {1}{2\cdot\sqrt y}$=$J_2$

➃we have $f_Y(y)$=$f_X(x)\cdot\frac {\operatorname dx}{\operatorname dy}$ in ➀ that we can now do the funny transform in between $Y$ and $Z$, to express $Y$ in terms of $Z_1$, $Z_2$.
$f_Y(y)$=$\frac {1}{\sqrt {2\cdot\pi}}\cdot e^{-\frac{y}{2}}\cdot\left|J_1\right|$+$\frac {1}{\sqrt {2\cdot\pi}}\cdot e^{-\frac{y}{2}}\cdot\left|J_2\right|$
$\;\;\;\;\;\;$=$\frac {1}{\sqrt {2\cdot\pi}}\cdot e^{-\frac{y}{2}}\cdot\left|-\frac {1}{2\cdot\sqrt y}\right|$+$\frac {1}{\sqrt {2\cdot\pi}}\cdot e^{-\frac{y}{2}}\cdot\left|\frac {1}{2\cdot\sqrt y}\right|$
$\;\;\;\;\;\;$=$\frac {1}{\sqrt {2\cdot\pi}}\cdot\frac {1}{\sqrt y}\cdot e^{-\frac{y}{2}}$
$\;\;\;\;\;\;$=$\frac {1}{\sqrt2\cdot\sqrt {\pi}}\cdot\frac {1}{\sqrt y}\cdot e^{-\frac{y}{2}}$
$\;\;\;\;\;\;$=$\frac {1}{2^{\frac {1}{2}}\cdot\sqrt {\pi}}\cdot y^{-\frac {1}{2}}\cdot e^{-\frac{y}{2}}$
$\;\;\;\;\;\;$=$\frac {1}{2^{\frac {1}{2}}\cdot\Gamma(\frac {1}{2})}\cdot y^{-\frac {1}{2}}\cdot e^{-\frac{y}{2}}$

➄we already know $\Gamma(\frac {1}{2})$=$\sqrt\pi$, this is quiet a beautiful deduction that it is just the PDF of gamma distribution with $\alpha=\frac {1}{2}$, $\beta=2$. $\frac {1}{2^{\frac {1}{2}}\cdot\Gamma(\frac {1}{2})}\cdot y^{-\frac {1}{2}}\cdot e^{-\frac{y}{2}}$ is just the chi-square PDF, Guess what?
$f(x)=\frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot x^{\frac \nu2 -1}\cdot e^{-\frac {x}{2}}$ with $\alpha=\frac {\nu}{2}$, $\nu=1$, $\beta=2$, for $x>0$.

Therefore, we just get $Z^2\sim\chi_1^2$ proved.

Sample Variance Evaluation Against Distribution Variance

Given $X_1$,$X_2$,$X_3$,…,$X_n\in N(\mu,\sigma^2)$, where each $X_i$ is an independent random variable, then:
$Z_i$=$\frac {X_i-\mu}{\sigma}$ is a standard normal distribution, $ɸ(0,1)$, for $i=1$ to $n$.

We have already proved $$Z^2\sim\chi_1^2$$, then, $$\sum_{i=1}^{n}Z_i^{2}\sim\chi_n^{2}$ could be obtained by mathematics induction. Suppose it is true and this proof would guide you through the relation in between sample variance and distribution variance.

proof:
➀expand from $Z_i^2$
$\sum_{i=1}^{n}Z_i^2$=$\sum_{i=1}^{n}(\frac {X_i-\mu}{\sigma})^2$
$\;\;\;\;\;\;\;\;$=$\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}+\overline{X_n}-\mu}{\sigma})^2$
$\;\;\;\;\;\;\;\;$=$\sum_{i=1}^{n}(\frac {(X_i-\overline{X_n})+(\overline{X_n}-\mu)}{\sigma})^2$
$\;\;\;\;\;\;\;\;$=$\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}}{\sigma})^2$+$\sum_{i=1}^{n}(\frac {\overline{X_n}-\mu}{\sigma})^2$+$2\cdot\sum_{i=1}^{n}\frac {(X_i-\overline{X_n})\cdot (\overline{X_n}-\mu)}{\sigma^2}$
, where $\overline{X_n}$ is the average for the whole $X_i’s$, for $i=1$ to $n$.

➁the final term is 0.
$\sum_{i=1}^{n}\frac {(X_i-\overline{X_n})\cdot (\overline{X_n}-\mu)}{\sigma^2}$
$=\frac {(\overline{X_n}-\mu)}{\sigma^2}\cdot\sum_{i=1}^{n}(X_i-\overline{X_n})=0$

Thus, we have it that:
$\sum_{i=1}^{n}Z_i^2$=$\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}}{\sigma})^2$+$\sum_{i=1}^{n}(\frac {\overline{X_n}-\mu}{\sigma})^2$

➂still focus on the final term.
$\sum_{i=1}^{n}(\frac {\overline{X_n}-\mu}{\sigma})^2$=$n\cdot (\frac {\overline{X_n}-\mu}{\sigma})^2$=$(\frac {\overline{X_n}-\mu}{\frac {\sigma}{\sqrt n}})^2$
Therefore, $\sum_{i=1}^{n}(\frac {\overline{X_n}-\mu}{\sigma})^2\approx Z_1^2\sim\chi_1^2$

Remember that we are under the assumption that $$\sum_{i=1}^{n}Z_i^{2}\sim\chi_n^{2}$ is true, then:
$\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}}{\sigma})^2+\chi_1^2\sim\chi_n^2$ must hold.
$\Rightarrow\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}}{\sigma})^2\sim\chi_{n-1}^2$ must hold.

➃in statistics, we denote sample variance as $S^2$ and have it that:
$S^2$=$\sum \frac {(X_i-\overline{X_n})^2}{n-1}$
$\Rightarrow (n-1)\cdot S^2=\sum (X_i-\overline{X_n})^2$
Therefore, $\frac {(n-1)\cdot S^2}{\sigma^2}\sim\chi_{n-1}^2$ is the final deduction result.

We can conclude that sample variance tested against normal distribution variance follows the $\chi_{n-1}^{2}$ distribution, with the assumption that the random sample of size $n$ is from $N(\mu,\sigma^2)$.

At the end of this article, it would be trivial that $\chi_n^2$=$\chi_{n-1}^2$+$\chi_1^2$ just holds.