Introduction To The F Distribution

05 Jan 2018

Prologue To The F Distribution

In probability theory and statistics, base on the most fundamental gamma distribution, F distribution is one of the many models of distributions further developed, furthermore, its definition is based on the chi-square distribution. With the basic realization of gamma, chi-square distributions, we could also treat the F distribution a special case of the gamma distribution. It would be greatly helpful in the evaluation of the regression model build on your hypothesis, the power of test for the precision in the machine learning results.

From The Chi-Square Distribution To The F Distribution

The model of F distribution is defined by the combination of two chi-square in ratio expression.
➀the definition is given by:
$F$=$\frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2}$, where $\chi_{\nu_i}^2$ is the chi-square PDF of DOF(degree of freedom) $\nu_i$, for $i=1,2$.

➁the F distribution PDF is expressed in below equality:
$h(f)$=$\frac {\Gamma(\frac {\nu_1+\nu_2}{2})\cdot (\frac {\nu_1}{\nu_2})^{\frac {\nu_1}{2}}}{\Gamma(\frac {\nu_1}{2})\cdot\Gamma(\frac {\nu_2}{2})}\cdot\frac {f^{\frac {\nu_1}{2}-1}}{(1+\frac {\nu_1}{\nu_2}\cdot f)^{\frac {\nu_1+\nu_2}{2}}}$

In the next paragraph, this article would prove &#10113 by means of the joint probability density function in conjunction with the integration by part.

The F Distribution And The Joint PDF

This section would like to detail the joint PDF for the F distribution model.

➀suppose $X$, $Y$ are two independent random variables with PDF $f_X(x)$, $f_Y(y)$.

➁let $Z$=$\frac {Y}{X}$, we denote $f_{XY}(x,y)$ to be the PDF of $Z$, where it is also a random variable. Then for all $x\in X$, $y\in Y$, $z\in Z$, we have it that:
$P(\frac {y}{x}\le z)$=$P(y\le z\cdot x)$

Therefore, $F_{XY}(z)$=$\int_0^{\infty}\int_{-\infty}^{z\cdot x}f_{XY}(x,y)\operatorname dy\operatorname dx$
, well, we can treat $Y\in \chi_{\nu_1}^2$, $X\in \chi_{\nu_2}^2$ by intuition, and $F_{XY}(z)$ is the CDF(cumulative distribution function).

➂let $y$=$x\cdot v$, then, $\operatorname dy$=$x\cdot\operatorname dv$, this is a little utilization of integration by part.
$F_{XY}(z)$=$\int_0^{\infty}\int_{-\infty}^{z}x\cdot f_{XY}(x,y)\operatorname dv\operatorname dx$
$\;\;\;\;\;\;\;\;$=$\int_{-\infty}^{z}\int_0^{\infty}x\cdot f_{XY}(x,y)\operatorname dx\operatorname dv$

➃derivate $F_{XY}(z)$ with respect to $v$, would we eliminate the term $\operatorname dv$, and express $f_{XY}(z)$, the PDF of F only in one term of $x$.
$f_{XY}(z)$=$\frac {\operatorname dF_{XY}(z)}{\operatorname dv}$
$\;\;\;\;\;\;\;\;$=$\int_0^{\infty}x\cdot f_{XY}(x,y)\operatorname dx$
$\;\;\;\;\;\;\;\;$=$\int_0^{\infty}x\cdot f_{XY}(x,x\cdot z)\operatorname dx$…take $v=z$
$\;\;\;\;\;\;\;\;$=$\int_0^{\infty}x\cdot f_{X}\cdot f_{Y}(x\cdot z)\operatorname dx$

➄let $X$, $Y$ now be the random variables in chi-square PDF with DOF=$n$, $m$ respectively, and recall that $Z$=$\frac {Y}{X}$, then:
$f_Z(z)$=$\int_0^{\infty}x\cdot\frac {x^{\frac {n}{2}-1}\cdot e^{-\frac {x}{2}}}{2^{\frac {n}{2}}\cdot\Gamma(\frac {n}{2})}\cdot\frac {(x\cdot z)^{\frac {m}{2}-1}\cdot e^{-\frac {x\cdot z}{2}}}{2^{\frac {m}{2}}\cdot\Gamma(\frac {m}{2})}\operatorname dx$
$\;\;\;\;\;\;\;\;$=$\frac {z^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}x^{\frac{m+n}{2}-1}\cdot e^{-\frac {x\cdot(z+1)}{2}}\operatorname dx$

➅let $t$=$\frac {x\cdot(z+1)}{2}$, then $\operatorname dt$=$\frac {z+1}{2}\cdot \operatorname dx$, and $x$=$\frac {2\cdot t}{z+1}$
$f_Z(z)$=$\frac {z^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}(\frac {2\cdot t}{z+1})^{\frac{m+n}{2}-1}\cdot e^{-t}\cdot\frac {2}{z+1}\operatorname dt$
$\;\;\;\;\;\;\;\;$=$\frac {z^{\frac {m}{2}-1}\cdot(\frac {2}{z+1})^{\frac {m+n}{2}}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}t^{\frac{m+n}{2}-1}\cdot e^{-t}\operatorname dt$
$\;\;\;\;\;\;\;\;$=$\frac {z^{\frac {m}{2}-1}\cdot\Gamma(\frac {m+n}{2})}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot (z+1)^{\frac {m+n}{2}}}$

The F Distribution PDF Deduction

Above section, ➅ leaves a useful expression of joint PDF of two chi-square in the form $Z$=$\frac {Y}{X}$, inheriting from it, we will continue to deduce it out for the Z distribution PDF.

➀let $Z$=$\frac {Y}{m}/\frac {X}{n}$ to meet F distribution definition, then for all $x\in X$, $y\in Y$, $z\in Z$, we have:
$z$=$\frac {y}{x}\cdot\frac {n}{m}$, $y$=$\frac {m}{n}\cdot x\cdot z$

➁this time, let $y$=$\frac {m}{n}\cdot x\cdot v$, then, $\operatorname dy$=$\frac {m}{n}x\cdot\operatorname dv$:
$F_{XY}(z)$=$\int_{-\infty}^{z}\int_0^{\infty}\frac {m}{n}\cdot x\cdot f_{XY}(x,y)\operatorname dx\operatorname dv$

➂Differentiate $F_{XY}(z)$ by $\operatorname dv$:
$f_{XY}(z)$=$\frac {\operatorname dF_{XY}(z)}{\operatorname dv}$
$\;\;\;\;\;\;\;\;$=$\frac {m}{n}\int_0^{\infty}x\cdot f_{XY}(x,\frac {m}{n}\cdot x\cdot z)\operatorname dx$…take $v=z$
$\;\;\;\;\;\;\;\;$=$\frac {m}{n}\int_0^{\infty}x\cdot f_{X}\cdot f_{Y}(\frac {m}{n}\cdot x\cdot z)\operatorname dx$
…replace $x\cdot z$ by $\frac {m}{n}\cdot x\cdot z$

➃because $f_Z(z)$=$f_{XY}(z)$, now we have it that:
$f_Z(z)$=$\frac {m}{n}\int_0^{\infty}x\cdot\frac {x^{\frac {n}{2}-1}\cdot e^{-\frac {x}{2}}}{2^{\frac {n}{2}}\cdot\Gamma(\frac {n}{2})}\cdot\frac {(\frac {m}{n}\cdot x\cdot z)^{\frac {m}{2}-1}\cdot e^{-\frac {\frac {m}{n}\cdot x\cdot z}{2}}}{2^{\frac {m}{2}}\cdot\Gamma(\frac {m}{2})}\operatorname dx$
$\;\;\;\;\;\;\;\;$=$\frac {\frac {m}{n}\cdot(\frac {m}{n}\cdot z)^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}x^{\frac{m+n}{2}-1}\cdot e^{-\frac {x}{2}\cdot(\frac {m}{m}\cdot z+1)}\operatorname dx$

➄let $t$=$\frac {x}{2}\cdot(\frac {m}{m}\cdot z+1)$, then we have it that:
$x$=$\frac {2\cdot t}{\frac {m}{n}\cdot z+1}$, $\operatorname dx$=$\frac {2\cdot t}{\frac {m}{n}\cdot z+1}\cdot\operatorname dt$
$f_Z(z)$=$\frac {\frac {m}{n}\cdot(\frac {m}{n}\cdot z)^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}(\frac {2\cdot t}{\frac {m}{n}\cdot z+1})^{\frac{m+n}{2}-1}\cdot e^{-t}\frac {2\cdot t}{\frac {m}{n}\cdot z+1}\cdot\operatorname dt$
$\;\;\;\;\;\;\;\;$=$\frac {\frac {m}{n}\cdot(\frac {m}{n}\cdot z)^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot(\frac {2}{\frac {m}{n}\cdot z+1})^{\frac{m+n}{2}}\cdot\int_0^{\infty}t^{\frac {m+n}{2}-1}\cdot e^{-t}\frac {2\cdot t}{\frac {m}{n}\cdot z+1}\cdot\operatorname dt$
$\;\;\;\;\;\;\;\;$=$\frac {\frac {m}{n}\cdot(\frac {m}{n}\cdot z)^{\frac {m}{2}-1}\cdot\Gamma(\frac {m+n}{2})}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot(\frac {m}{n}\cdot z+1)^{\frac{m+n}{2}}}$
$\;\;\;\;\;\;\;\;$=$\frac {(\frac {m}{n})^{\frac {m}{2}}\cdot z^{\frac {m}{2}-1}\cdot\Gamma(\frac {m+n}{2})}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot(\frac {m}{n}\cdot z+1)^{\frac{m+n}{2}}}$
, where $X$, $Y$ are the random variables in chi-square PDF with DOF=$n$, $m$ respectively, and recall that $Z$=$\frac {Y}{m}/\frac {X}{n}$

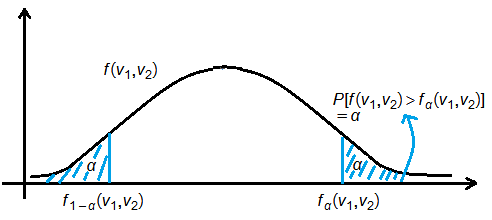
The F Distribution Features

➀$f(\nu_1,\nu_2)$=$\frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2}$=$1/\frac {\frac {\chi_{\nu_2}^2}{\nu_2}}{\frac {\chi_{\nu_1}^2}{\nu_1}}$=$\frac {1}{f(\nu_2,\nu_1)}$

➁$f_{1-\alpha}(\nu_2,\nu_1)$=$\frac {1}{f_{\alpha}(\nu_1,\nu_2)}$, let’s see why.

$\Rightarrow P\lbrack f(\nu_1,\nu_2)<f_\alpha(\nu_1,\nu_2)\rbrack$=$1-\alpha$
$\Rightarrow P\lbrack \frac {1}{f(\nu_2,\nu_1)}<f_\alpha(\nu_1,\nu_2)\rbrack$=$1-\alpha$
$\Rightarrow P\lbrack \frac {1}{f_\alpha(\nu_1,\nu_2)}<f(\nu_2,\nu_1)\rbrack$=$1-\alpha$
$\Leftrightarrow P\lbrack f(\nu_2,\nu_1)>f_{1-\alpha}(\nu_2,\nu_1)\rbrack$=$1-\alpha$
therefore, we have $f_{1-\alpha}(\nu_2,\nu_1)$=$\frac {1}{f_\alpha(\nu_1,\nu_2)}$

Expect Value Of The F Distribution

By definition, $F$=$\frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2}$
➀for all $f \in F$, to ask for its expect value:
$E\lbrack f\rbrack$=$E\lbrack \frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2}\rbrack$
$\;\;\;\;\;\;$=$\frac {\nu_2}{\nu_1}\cdot E\lbrack \frac {\chi_{\nu_1}^2}{\chi_{\nu_2}^2}\rbrack$
$\;\;\;\;\;\;$=$\frac {\nu_2}{\nu_1}\cdot E\lbrack \chi_{\nu_1}^2\rbrack\cdot E\lbrack \frac {1}{\chi_{\nu_2}^2}\rbrack$
, where we have $E\lbrack \chi_{\nu_1}^2\rbrack$=$\nu_1$, next for $E\lbrack \frac {1}{\chi_{\nu_2}^2}\rbrack$.

➁for all $x \in \chi_{\nu_2}^2$,
$E\lbrack \frac {1}{\chi_{\nu_2}^2}\rbrack$=$\int_0^{\infty}\frac {1}{x}\cdot\frac {x^{\frac {\nu_2}{2}-1}\cdot e^{-\frac {x}{\beta}}}{\beta^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\operatorname dx$
$\;\;\;\;\;\;$=$\int_0^{\infty}\frac {1}{x}\cdot\frac {x^{\frac {\nu_2}{2}-1}\cdot e^{-\frac {x}{2}}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\operatorname dx$, where $\beta$=$2$

➂to eliminate the complexity and try to express in terms of $\Gamma(\alpha)$,
let $y$=$\frac {x}{2}$, then we have $2\cdot\operatorname dy$=$\operatorname dx$,
$\Rightarrow\int_0^{\infty}\frac {1}{2\cdot y}\cdot\frac {(2\cdot y)^{\frac {\nu_2}{2}-1}\cdot e^{-\frac {x}{2}}\cdot 2}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\operatorname dy$
$=\frac {2^{\frac {\nu_2}{2}-1}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\int_0^{\infty}y^{(\frac {\nu_2}{2}-1)-1}\cdot e^{-y}\operatorname dy$
$=\frac {1}{2\cdot\Gamma(\frac {\nu_2}{2})}\cdot\Gamma(\frac {\nu_2}{2}-1)$
$=\frac {\Gamma(\frac {\nu_2}{2}-1)}{2\cdot(\frac {\nu_2}{2}-1)\cdot\Gamma(\frac {\nu_2}{2}-1)}$
$=\frac {1}{\nu_2-2}$

Therefore, $E\lbrack f\rbrack$=$\frac {\nu_2}{\nu_1}\cdot\nu_1\cdot\frac {1}{\nu_2-2}$=$\frac {\nu_2}{\nu_2-2}$

Moments Of The F Distribution

Before the variance of F distribution, by using the k-th ordinary moment could we speed up and be recalled that we have used it in the article of chi-square distribution.
➀for all $x \in \chi_{\nu_2}^2$
$E_r\lbrack\frac {1}{\chi_{\nu_2}^2}\rbrack$=$\int_0^{\infty}\frac {1}{x^r}\cdot\frac {x^{\frac {\nu_2}{2}-1}\cdot e^{-\frac {x}{2}}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\operatorname dx$

➁let $y$=$\frac {x}{2}$, then $x$=$2\cdot y$, $\operatorname dx=2\cdot\operatorname dy$
$\Rightarrow\int_0^{\infty}\frac {1}{(2\cdot y)^r}\cdot\frac {(2\cdot y)^{\frac {\nu_2}{2}-1}\cdot e^{-y}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\cdot 2\cdot\operatorname dy$
$=\frac {2\cdot 2^{-r}\cdot 2^{\frac {\nu_2}{2}-1}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\cdot\int_0^{\infty}y^{-r}\cdot y^{\frac {\nu_2}{2}-1}\cdot e^{-y}\operatorname dy$
$=\frac {2^{-r}}{\Gamma(\frac {\nu_2}{2})}\cdot\int_0^{\infty}y^{\frac {\nu_2}{2}-r-1}\cdot e^{-y}\operatorname dy$
$=\frac {2^{-r}}{\Gamma(\frac {\nu_2}{2})}\cdot\Gamma(\frac {\nu_2}{2}-r)$

➂for $r=1$, $\mu_1$, we have it that:
$E_1\lbrack\frac {1}{\chi_{\nu_2}^2}\rbrack$
$=\mu_1$
$=\frac {2^{-1}}{\Gamma(\frac {\nu_2}{2})}\cdot\Gamma(\frac {\nu_2}{2}-1)$
$=\frac {2^{-1}}{(\frac {\nu_2}{2}-1)\cdot\Gamma(\frac {\nu_2}{2}-1)}\cdot\Gamma(\frac {\nu_2}{2}-1)$
$=\frac {1}{\nu_2-2}$

➃for $r=2$, $\mu_2$, we have it that:
$E_2\lbrack\frac {1}{\chi_{\nu_2}^2}\rbrack$
$=\mu_2$
$=\frac {2^{-2}}{\Gamma(\frac {\nu_2}{2})}\cdot\Gamma(\frac {\nu_2}{2}-2)$
$=\frac {2^{-2}}{(\frac {\nu_2}{2}-1)\cdot(\frac {\nu_2}{2}-2)\cdot\Gamma(\frac {\nu_2}{2}-2)}\cdot\Gamma(\frac {\nu_2}{2}-2)$
$=\frac {1}{2^2\cdot\frac {\nu_2-2}{2})\cdot(\frac {\nu_2-4}{2})}$
$=\frac {1}{(\nu_2-2)\cdot(\nu_2-4)}$

Variance Of The F Distribution

Succeeding to results of moments from above paragraph, we proceed to ask for the variance of F distribution. Please recall that we have the 2nd ordinary moment of the chi-square $E_2\lbrack(\chi_{\nu}^2)^2\rbrack=\nu^2+2\cdot\nu$.

➀$Var\lbrack f\rbrack$=$E\lbrack f^2\rbrack$-$E^2\lbrack f\rbrack$, next to figure out $E\lbrack f^2\rbrack$

$E\lbrack f^2\rbrack$
$=E\lbrack (\frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2})^2\rbrack$
$=(\frac {\nu_2}{\nu_1})^2\cdot E\lbrack (\frac {\chi_{\nu_1}^2}{\chi_{\nu_2}^2})^2\rbrack$
$=(\frac {\nu_2}{\nu_1})^2\cdot E\lbrack (\chi_{\nu_1}^2)^2\rbrack\cdot E\lbrack (\frac {1}{\chi_{\nu_2}^2})^2\rbrack$
$=(\frac {\nu_2}{\nu_1})^2\cdot(\nu_1^2+2\cdot\nu_1)\cdot\frac {1}{(\nu_2-2)\cdot(\nu_2-4)}$
$=\frac {\nu_2^2}{\nu_1}\cdot(\nu_1+2)\cdot\frac {1}{(\nu_2-2)\cdot(\nu_2-4)}$

➁therefore, the variance could now be expressed:
$Var\lbrack f\rbrack$
$=E\lbrack f^2\rbrack$-$E^2\lbrack f\rbrack$
$=\frac {\nu_2^2}{\nu_1}\cdot(\nu_1+2)\cdot\frac {1}{(\nu_2-2)\cdot(\nu_2-4)}$-$(\frac {\nu_2}{\nu_2-2})^2$
$=\frac {\nu_2^2\cdot(\nu_1+2)\cdot(\nu_2-2)}{\nu_1\cdot(\nu_2-2)^2\cdot(\nu_2-4)}$-$\frac {\nu_1\cdot\nu_2^2\cdot(\nu_2-4)}{\nu_1\cdot(\nu_2-2)^2\cdot(\nu_2-4)}$
$=\frac {2\cdot\nu_2^2\cdot(\nu_1+\nu_2-2)}{\nu_1\cdot(\nu_2-2)^2\cdot(\nu_2-4)}$
, where $\nu_2>4$ is the condition, it must hold!!!