Introduction To The Bayesian Network

08 Jul 2018

Prologue To Introduction To The Bayesian Network

A Bayesian network is a model of a system, consisting of a number of random varaibles. It provides much more information than simple classifier(like neural networks, support vector machines), when used, the Bayesian network comes out with the probability distribution of the values of the random variable to be predicted.

What is a Bayesian Network?

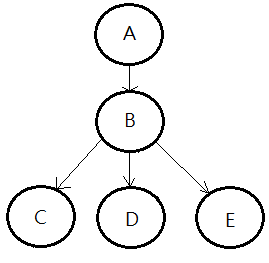
We begin by a simple graph illustration:
➀we can treat the it as a structured, graphical representation of probabilistic relationships between several random variables.
➁it explicitly encodes the conditional independences by the missing arcs.
➂it can efficiently represent the joint PDF(probability distribution function) of the whole network or the combinatorial random variables in the model.
➃it is a generative model, which allows arbitrary queries to be answered.

The Conditional Independence Relationship

In my previous article Introduction To The Conditional Probability, I have guided you through the conditional dependence. This article would then step into the field of conditional independence.

[1] Conditional independence axioms

A tutorial on Bayesian belief networks, Mark L Krieg, p.3 briefly describes the axiomatic basics for the conditional independence, which is in turn from the paper by Pearl, 1988.

Let $X$,$Y$,$Z$ denote any 3 distinct subsets of variables in the universe, called $U$. We define $I(X,Y,Z)_p$ to represent the conditional independence of $X$ from $Y$, given $Z$ in the probabilistic model $p$.
$\;\;I(X,Y,Z)_p$, iff $P(x\vert z,y)$=$P(x\vert z)$ and $P(y)>0$.

The following relationships holds:
➀$I(X,Z,Y)_p$
$\Leftrightarrow P(x,y\vert z)$=$P(x\vert z)\cdot P(y\vert z)$
➁$I(X,Z,Y)_p$
$\Leftrightarrow P(x,y,z)$=$P(x\vert z)\cdot P(y,z)$
➂$I(X,Z,Y)_p$
$\Leftrightarrow\;\exists f,g: P(x,y,z)$=$f(x,z)\cdot g(y,z)$, where $f,g$ are arbitrary functions of conditional probability or joint probability.

Above 3 equilibrium are based on the model that $X$ is the descendent of $Z$, where $Y$ is some unrelated node to both $X$,$Z$.

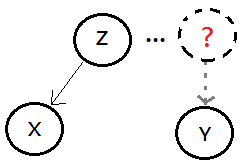
[2] 3 dependencies

They could be treated as 3 types of connections in the Bayesian network, they are:
➀serial connection, knowing $B$ makes $A$ and $C$ independent, this is the intermediate cause.
➁diverging connection, knowing $B$ makes $A$ and $C$ independent, this is the common cause.
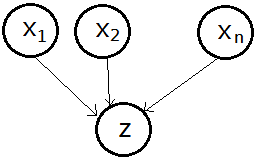
➂converging connection, this is the common effect, not knowing $Y$ makes $X_{1}$,$X_{2}$,...,$X_{n}$ independent.

The Bayesian Network=$(G,\Theta)$

In this article, we define $(G,\Theta)$ of the Bayesian networks to be the graphic representation of models capturing the relationships in between model’s variables, where:
➀$G$ is the DAG(directed acyclic graphic) containing nodes connected by arcs with arrows, the nodes are the random variables, the direction of arcs begins from parent node(s) to its descendent nodes, the child node depends on its parent node.
➁$\Theta$ is the set of parameters in all conditional probability distributions.

Where the DAG is the graphic containing no node of self-recycling path.

The Joint Probability Distribution Of Bayesian Network

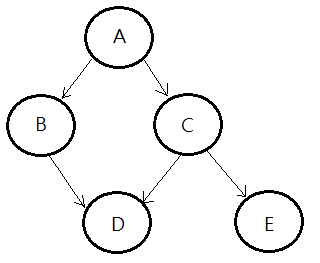
Continue to use above DAG, I’d like to compute the joint probability of all random variables in this Bayesian network, I’m going to illustrate each step of proof:

proof::mjtsai1974

[1]By chain rule, we have:
$P(A,B,C,D,E)$
=$P(E\vert D,C,B,A)$
$\;\;\cdot P(D\vert C,B,A)$
$\;\;\cdot P(C\vert B,A)$
$\;\;\cdot P(B\vert A)$
$\;\;\cdot P(A)$

[2]By the conditional independence in this model, we can further simplify these terms:
➀$P(E\vert D,C,B,A)$=$P(E\vert C)$
➁$P(D\vert C,B,A)$=$P(D\vert C,B)$
➂$P(C\vert B,A)$=$P(C\vert A)$
➃therefore, the full joint probability is thus expressed:
$P(A,B,C,D,E)$
=$P(E\vert C)$
$\;\;\cdot P(D\vert C,B)$
$\;\;\cdot P(C\vert A)$
$\;\;\cdot P(B\vert A)$
$\;\;\cdot P(A)$

The Number Of Parameters In The Bayesian Network

In the Bayesian network, each node represents a random variable, each arc encodes the conditional dependency in between parent and child nodes.

Succeeding to the same DAG, I’d like to decode out the number of parameters encoded in the conditional dependencies in the model, to which the network is trying to approximate.
➀the parameters are not equivalent to the nodes of random variables.
➁the parameters are the compounded conditioning events, depicted in below graph.
➂totally, $1$+$2$+$2$+$4$+$2$, there are $11$ parameters in this probabilistic model of network, compared to the multinomial distruibution, in this case $2^{5}-1$=$31$ parameters.

Such a reduction provides benefits from inference, learning(parameter estimation) and compuutation perspective.

The Concept Of D-Separation

[1] d-separated

Nodes $X$ and $Y$ are d-separated, if on any (undirected)path in between $X$ and $Y$, there exists some random variable $Z$, such that:
➀$Z$ is in a series or diverging connection and $Z$ is known, or
➁$Z$ is in a converging connection, neither $Z$ nor any of its descendent(s) $W$ is known.
There is one alternative condition, that $Z$ is not known, $X$, $Y$ and $W$ are all d-separated.

[2] d-connected

Nodes $X$ and $Y$ are d-connected, if they are not d-separated. The most trivial example is that $Y$ is the descendent of $X$.

[3] conditional independence

Nodes $X$ and $Y$ are d-separated by $Z$, then they are conditionally independent given $Z$.

Addendum

➀A tutorial on Bayesian belief networks, Mark L Krieg
➁A tutorial on learning and inference in the Bayesian networks, Irina Rish