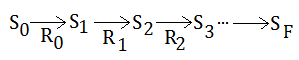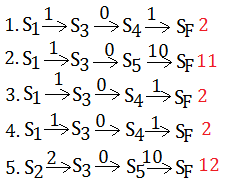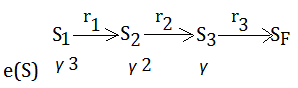Temporal Difference Learning - Part 1
23 Dec 2018Prologue To The Temporal Difference Learning - Part 1
Begin By Intuition
Given below state transition, where $R_{i}$ is the immediate reward associated with $S_{i}$, and we try to predict the expected sum of discounted rewards by TD($\lambda$).
ReCap The Backup In Markov Chain
[Question]Given this Markov chain, where all states are initialized with value $0$, and $S_{3}$ is stochastic with $0.9$ to $S_{4}$, $0.1$ to $S_{5}$.
[Answer]
For $S_{F}$ is the state we end up in, this final state is set to $0$ in its value. As to other states, it’s the expected value of the reward plus the discounted value of the state we end up in.
$V(S)$=
➀$0$ for $S_{F}$.
➁$E\lbrack R_{i}+\gamma\cdot V(S’)\rbrack$, $S’$ is the state we arrive in.
The immediate reward associated are $+1$ with $S_{1}$, $+2$ with $S_{2}$, $0$ with $S_{3}$, $+1$ with $S_{4}$ and $+10$ with $S_{5}$. Let discounted factor $\gamma$=$1$, what is V($S_{3}$)?We’d like to use the backup propagation to figure out the value function of these states:
➀V($S_{4}$)=$1$+$\gamma\cdot 1\cdot 0$=$1$
➁V($S_{5}$)=$10$+$\gamma\cdot 1\cdot 0$=$10$
➂V($S_{3}$)=$0$+$\gamma\cdot(0.9\cdot 1+0.1\cdot 10)$
=$1.9$, where $\gamma$=$1$
➃V($S_{1}$)=$1$+$\gamma\cdot 1\cdot 1.9$=$2.9$
➄V($S_{2}$)=$2$+$\gamma\cdot 1\cdot 1.9$=$3.9$
Estimate From Data In Example
[Question]Given the same Markov chain with $\gamma$=$1$, this is the simulation before we know the whole image of the model.
We'd like to estimate the value of $S_{1}$ after 3 and 4 episodes
, since nothing related to $S_{2}$, just ignore it.
[Hints]::by mjtsai1974The red marked numbers are the value of $S_{1}$ in each episode. By using backup or expect discounted reward could we obtain the same value function of states, even for $\gamma$=$0.9$. Let me do the illustrtation of the 1st episode.
[Answer]
[1]by using backup:
➀$V(S_{4})$=$1+\gamma\cdot 1\cdot 0$
$V(S_{4})$=1 for $\gamma$=$1$ and $0.9$, where $\gamma\cdot 1$, this 1 is the probabilistic transition, since it's the only one path, the probability is $1$.
➁$V(S_{3})$=$0+\gamma\cdot V(S_{4})$
$V(S_{3})$=$1$ for $\gamma$=$1$ and $0.9$ for $\gamma$=$0.9$
➂$V(S_{1})$=$1+\gamma\cdot V(S_{3})$
$V(S_{1})$=$2$ for $\gamma$=$1$ and $1.81$ for $\gamma$=$0.9$
[2]by using expect discounted reward:
➀$V(S_{1})$ expression
=$1$+$\gamma\cdot 1\cdot(0+\gamma\cdot 1\cdot(1+\gamma\cdot 1\cdot 0))$
, where $V(S_{1})$=$2$ for $\gamma$=$1$ and $1.81$ for $\gamma$=$0.9$The appropriate estimate for $V(S_{1})$ after 3 and 4 episodes would be $\frac {2+11+2}{3}$=$5$ and $\frac {2+11+2+2}{4}$=$4.25$ respectively.
To estimate from data is asking to do an expectation, it is just averaging things. We can incrementally compute an estimate for the value of a state, given the previous estimate.
But, it is a big jump for $V(S_{1})$ from $5$ to $4.25$, when it is estimated from eposide 3 to 4. With an inifinite amount of data in an already known Markov chain model, we should get $V(S_{1})$=$2.9$, which is the converged value, could be found in above section ReCap The Backup In Markov Chain.
Because, not enough data, just 3 episodes, an over-representation of the higher reward, that’s why we have higher skewed estimate of $5$ than $4.25$ in 4 episodes.
Computing Estimates Incrementally
[Question]From prior example, we have the value of $S_{1}$=$5$, say $V_{3}(S_{1})$ after 3 episodes, then we ran an eposide, and the return of the episode, the total discounted reward of $S_{1}$ in this distinct 4-th sequence was $2$, say $R_{4}(S_{1})$.
Could we figure out what the new estimate of value of $S_{1}$, say $V_{4}(S_{1})$, just from this information?
[Answer]By weighting, $\frac {3\cdot 5 + 1\cdot 2}{4}$=$4.25$, we could get the same estimate identical to the way of expectation.
[The generalization]Can we generalize it? Yes!
$V_{T}(S_{1})$
=$\frac {(T-1)\cdot V_{T-1}(S_{1})+1\cdot R_{T}(S_{1})}{T}$
=$\frac {(T-1)\cdot V_{T-1}(S_{1})}{T}$+$\frac {1\cdot R_{T}(S_{1})}{T}$
=$\frac {(T-1)\cdot V_{T-1}(S_{1})}{T}$+$\frac {V_{T-1}(S_{1})}{T}$+$\frac {1\cdot R_{T}(S_{1})}{T}$-$\frac {V_{T-1}(S_{1})}{T}$
=$V_{T-1}(S_{1})$+$\alpha_{T}\cdot (R_{T}(S_{1})-V_{T-1}(S_{1}))$
, where we have it that:
➀$\alpha_{T}$=$\frac {1}{T}$, the learning rate(parameter)
➁the temporal difference is the difference between the reward we get at this step and the estimate we had at th eprevious step.
➂$R_{T}(S_{1})-V_{T-1}(S_{1})$ is the error term. If the difference is zero, then no change; if the difference is (big) positive, then, it goes up; if the difference is big negative, then, it goes down.As we get more and more eposides, this learning parameter $\alpha_{T}$ is getting small and small, and making smaller and smaller changes. It’s just like the update rule in perceptrons learning and neural network learning.
The Property Of Learning Rate
By given $V_{T}(S)$=$V_{T-1}(S)$+$\alpha_{T}\cdot(R_{T}(S)-V_{T-1}(S))$, then, $\lim_{T\rightarrow\infty}V_{T}(S)$=$V(S)$, with below 2 properties guarantee the convergence:
proof::mjtsai1974
➀$\sum_{T=0}^{\infty}\alpha_{T}\rightarrow\infty$
➁$\sum_{T=0}^{\infty}(\alpha_{T})^{2}<\infty$I’d like to prove the learning rate property by using geometric series convergence/divergence by Gilbert Strange in Calculus.
➀begin from $T$=$0$, initially $V_{0}(S)$=$C$, some constant, might be zero. And $V_{T}(S)$=$V_{T-1}(S)$=$V_{0}(S)$ at this moment.
➁suppose the equality holds, then expand from $T+1$:
$V_{T+1}(S)$
=$V_{T}(S)$+$\alpha_{T}\cdot(R_{T+1}(S)-V_{T}(S))$
=$V_{T}(S)$+$\alpha_{T}\cdot(R_{T+1}(S)-(V_{T-1}(S)$+$\alpha_{T}\cdot(R_{T}(S)-V_{T-1}(S))))$
=$V_{T}(S)$+$\alpha_{T}\cdot(R_{T+1}(S)-(V_{T-1}(S)$+$\alpha_{T}\cdot(R_{T}(S)-(V_{T-2}(S)$+$\alpha_{T}\cdot(R_{T-1}(S)-V_{T-2}(S))))))$
➂the expand could be continued, but we stop over here for our proof…
=$V_{T}(S)$+$\alpha_{T}\cdot(R_{T+1}(S)-V_{T-1}(S))$
$\;\;$+$\alpha_{T}^{2}\cdot(R_{T}(S)-V_{T-2}(S))$
$\;\;$+$\alpha_{T}^{3}\cdot(R_{T-1}(S)-V_{T-2}(S))$
➃to make it perfect, expand the term $V_{T-2}(S)$, we can get it down the way to $T=0$:
=$V_{T}(S)$+$\alpha_{T}\cdot(R_{T+1}(S)-V_{T-1}(S))$
$\;\;$+$\alpha_{T}^{2}\cdot(R_{T}(S)-V_{T-2}(S))$
$\;\;$+$\alpha_{T}^{3}\cdot(R_{T-1}(S)-V_{T-3}(S))$
$\;\;$+$\alpha_{T}^{4}\cdot(R_{T-2}(S)-V_{T-4}(S))$
$\;\;$+$\alpha_{T}^{5}\cdot(R_{T-3}(S)-V_{T-5}(S))$+…
➄we take $E_{1}$=$R_{T+1}(S)-V_{T-1}(S)$
$\;\;\;\;E_{2}$=$R_{T}(S)-V_{T-2}(S)$
$\;\;\;\;E_{3}$=$R_{T-1}(S)-V_{T-3}(S)$
… , where each $E_{i}$ is a constant, assume they are rather stable, non-variant, then we take these error terms as $E$.
➅then, the whole terms after the first + operator could be expressed as:
$\alpha_{T}\cdot E$+$\alpha_{T}^{2}\cdot E$+$\alpha_{T}^{3}\cdot E$+$\alpha_{T}^{4}\cdot E$+…
=$(\alpha_{T}+\alpha_{T}^{2}+\alpha_{T}^{3}+\alpha_{T}^{4}+…)\cdot E$
=$(\lim_{k\rightarrow\infty}\sum_{i=1}^{k}\alpha_{T}^{i})\cdot E$, then,
$\lim_{k\rightarrow\infty}\sum_{i=1}^{k}\alpha_{T}^{i}$=$\frac {\alpha_{T}}{1-\alpha_{T}}$, for $\left|\alpha_{T}\right|$<$1$, and it holds to have these 2 properties, it is the convergent series, you can see in my prior post Series Convergence.
The $TD(\lambda)$ Algorithm
[The rule]Eposide $T$:
[Notes]
$\;\;$For all $S$, $e(S)$=$0$ at start of eposide, $V_{T}(S)$=$V_{T-1}(S)$
$\;\;$After $S_{t-1}\xrightarrow{r_{t}}S_{t}$:(from step $t-1$ to $t$ with reward $r_{t}$)
$\;\;\;e(S_{t-1})$=$e(S_{t-1})$+$1$:
$\;\;\;\;$Update eligibility of $S_{t-1}$ after arriving to $S_{t}$
$\;\;$For all $S$,
$\;\;V_{T}(S)$=$V_{T-1}(S)$+$\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1}))$
$\;\;\;e(S_{t-1})$=$\lambda\cdot\gamma\cdot e(S_{t-1})$:
$\;\;\;\;$before transite from $S_{t-1}$ to $S_{t}$ in next iterationWhere the $T$ stands for the specific eposide, $t$ is the index for state transition, and $e(S_{t})$ is for the eligibility.
$TD(1)$ Algorithm: $\lambda$=$1$
This is by taking $\lambda$=$1$ in $TD(\lambda)$ algorithm.
[The rule]Eposide $T$:
[Notes]
$\;\;$For all $S$, $e(S)$=$0$ at start of eposide, $V_{T}(S)$=$V_{T-1}(S)$
$\;\;$After $S_{t-1}\xrightarrow{r_{t}}S_{t}$:(from step $t-1$ to $t$ with reward $r_{t}$)
$\;\;\;e(S_{t-1})$=$e(S_{t-1})$+$1$:
$\;\;\;\;$Update eligibility of $S_{t-1}$ after arriving to $S_{t}$
$\;\;$For all $S$,
$\;\;V_{T}(S)$=$V_{T-1}(S)$+$\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1}))$…[A]
$\;\;\;e(S_{t-1})$=$\gamma\cdot e(S_{t-1})$:
$\;\;\;\;$before transite from $S_{t-1}$ to $S_{t}$ in next iteration➀the 2nd part of [A] is sum of the reward plus the the discounted value of the state we just arrived, minus the state value we just left; where these state values are all evaluated in last iteration. It could just be the temporal difference.
[Caution]
➁we are going to apply the temporal difference onto all states, proportional to the eligibility of each distinct state, and the learning rate would be specified for we don’t want it to move too much.
➂after the state has been iterated, decay or decrease its eligibility with $\lambda\cdot\gamma$, in their given value, in $TD(1)$, $\lambda$=$1$.
➃and we are backing up to next state.➀all the $S$ are all being done in similar approach.
➁the value at state $S$(the $S$ in (A)) is going to be updated on this quantity, $r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1})$, which is the same for everybody, doesn't depend on which $S$ we are updating, and $e(S)$ is specific to the state $S$ we are evaluating(looking at).
Example: $TD(1)$ Illustration
[1] Keeping track of changes ultimatelyLet’s walk through the pseudo code in this given example, just to see how value update works.
[2] The expression of the update
➀we are starting off at the beginning of an eposide. Now, the eligibility for all states are all zero.
➁we’d like to keep track of changes ultimately, it’s all going to get added to whatever the previous value.
➂the 1st transition is from $S_{1}$ to $S_{2}$ with reward $r_{1}$, and sets the eligibility $e(S_{1})$ to 1 for $S_{1}$.
➃we’d like to loop through all the states, all of them, and apply the same little update to all of the states.The update has the form:
[3] The update from $S_{1}$ to $S_{2}$
➀whatever the current learning rate is, times the reward which we just experienced, say $r_{1}$, plus the discount factor gamma $\gamma$ times the previous value of the state we newly arrived, minus the the previous value of the state we just left.
➁$\alpha_{T}\cdot(r_{t}+\gamma\cdot V_{T-1}(S_{t})-V_{T-1}(S_{t-1}))$, it is going to get added to all states, such quantity is proportional to the eligibility of that state.After transiting from $S_{1}$ to $S_{2}$, at this moment, the eligibility of $S_{2}$ and $S_{3}$ are $0$, we are only making updating with respect to $S_{1}$.
Before next step from $S_{2}$ to $S_{3}$, be sure to decay current evaluated state $S_{1}$'s eligibility by $\gamma$.
➀$\triangle V_{T}(S_{1})$=$\alpha\cdot(r_{1}+\gamma\cdot V_{T-1}(S_{2})-V_{T-1}(S_{1}))$, where $\alpha_{T}$=$\alpha$ wichi is a constant all the way.
➁$\triangle V_{T}(S_{2})$=$0$
➂$\triangle V_{T}(S_{3})$=$0$[4] The update from $S_{2}$ to $S_{3}$
This is the eligibility after $S_{1}$ to $S_{2}$.
We take next step from $S_{2}$ to $S_{3}$ with reward $r_{2}$. It bumps $S_{2}$'s eligibility from $0$ to $1$.
Before next step from $S_{3}$ to $S_{F}$, be sure to decay current already evaluated states $S_{1}$ and $S_{2}$'s eligibility by $\gamma$.
Current eligibility at this moment are $\gamma$,$1$,$0$ for $S_{1}$,$S_{2}$,$S_{3}$. The update term $\alpha\cdot(r_{2}+\gamma\cdot V_{T-1}(S_{3})-V_{T-1}(S_{2}))$, is independent of which state we are actually changing, we are going to apply it with respect to each state's($S_{1}$,$S_{2}$) eligibility, proportionally.
➀$\triangle V_{T}(S_{1})$
=$\alpha\cdot(r_{1}+\gamma\cdot V_{T-1}(S_{2})-V_{T-1}(S_{1}))$
$\;\;+\gamma\cdot\alpha\cdot(r_{2}+\gamma\cdot V_{T-1}(S_{3})-V_{T-1}(S_{2}))$
=$\alpha\cdot(r_{1}+\gamma\cdot r_{2}+\gamma^{2}\cdot V_{T-1}(S_{3})-V_{T-1}(S_{1}))$
➁$\triangle V_{T}(S_{2})$=$\alpha\cdot(r_{2}+\gamma\cdot V_{T-1}(S_{3})-V_{T-1}(S_{2}))$
➂$\triangle V_{T}(S_{3})$=$0$[5] The update from $S_{3}$ to $S_{F}$
This is the eligibility after $S_{2}$ to $S_{3}$.
Finally, we take next step from $S_{3}$ to $S_{F}$ with reward $r_{3}$. It bumps $S_{3}$'s eligibility from $0$ to $1$. Current eligibility at this moment are $\gamma^{2}$,$\gamma$,$1$ for $S_{1}$,$S_{2}$,$S_{3}$.
The update term $\alpha\cdot(r_{3}+\gamma\cdot V_{T-1}(S_{F})-V_{T-1}(S_{3}))$, is independent of which state we are actually changing, we are going to apply it with respect to each state's($S_{1}$,$S_{2}$,$S_{3}$) eligibility, proportionally.
➀$\triangle V_{T}(S_{1})$
=$\alpha\cdot(r_{1}+\gamma\cdot V_{T-1}(S_{2})-V_{T-1}(S_{1}))$
$\;\;+\gamma\cdot\alpha\cdot(r_{2}+\gamma\cdot V_{T-1}(S_{3})-V_{T-1}(S_{2}))$
$\;\;+\gamma^{2}\cdot\alpha\cdot(r_{3}+\gamma\cdot V_{T-1}(S_{F})-V_{T-1}(S_{3}))$
=$\alpha\cdot(r_{1}+\gamma\cdot r_{2}+\gamma^{2}\cdot r_{3}+\gamma^{3}\cdot V_{T-1}(S_{F})-V_{T-1}(S_{1}))$
➁$\triangle V_{T}(S_{2})$
=$\alpha\cdot(r_{2}+\gamma\cdot V_{T-1}(S_{3})-V_{T-1}(S_{2}))$
$\;\;+\gamma\cdot\alpha\cdot(r_{3}+\gamma\cdot V_{T-1}(S_{F})-V_{T-1}(S_{3}))$
=$\alpha\cdot(r_{2}+\gamma\cdot r_{3}+\gamma^{2}\cdot V_{T-1}(S_{F})-V_{T-1}(S_{2}))$
➂$\triangle V_{T}(S_{3})$=$\alpha\cdot(r_{3}+\gamma\cdot V_{T-1}(S_{F})-V_{T-1}(S_{3}))$Where we have the value of the state $S_{F}$ as $0$, at this ending, even no next state to jump to, we should also decrease each state's eligibility by $\gamma$.
[Notes]
➀$TD(1)$ is the same as the outcome-base update, that is to say we want to see all the discounted rewards on the entire trajectory, and we just update our prediction of the state that they started from with those rewards.
➁in this article, we are talking about the discounted sum of rewards minus the old prediction(evaluated in the last episode $T-1$).
Example: $TD(1)$ Illustration In Repeated States
[The case of repeated states][But, mjtsai's viewpoint]
If we follow up $TD(1)$ rule, you might get:
$\triangle V_{T}(S_{F})$=$\alpha\cdot(r_{1}’$+$\gamma\cdot V_{T-1}(S_{F})-V_{T-1}(S_{1}))$
➀the online course said that it a mistake, for you go to $S_{1}$, you saw $S_{1}$ transite to $S_{2}$ with $r_{1}$, therefore you just ignore anything you learned along the way.
➁the $TD(1)$ rule lets you do is, when you see $S_{1}$ again, and sort of backup its value, you’re actually capturing the fact the last time you were in $S_{1}$, you actually went to $S_{2}$ and saw $r_{1}$.
➂it’s just like outcome-base on updates, now with extra learning or inside the eposide learning from head of the trajectory.Suppose you have just completed the 1st run and reach $S_{F}$, now you are transiting to $S_{1}$ again, the eligibility of all states and state transition diagram are given in below:
Such eligibility is not yet in the ending of this transition, it is in the beginning. If you complete the transition and would like to start to transit from $S_{1}$ to $S_{2}$, be sure to remember to decay all the eligibility by $\gamma$, guess what, it should be $\gamma^{4}$,$\gamma^{3}$,$\gamma^{2}$,$\gamma$ for $S_{1}$,$S_{2}$,$S_{3}$,$S_{F}$.
➀the update term of $S_{F}$ in eposide $T$:
$\triangle V_{T}(S_{F})$=$\alpha\cdot(r_{1}’$+$\gamma\cdot V_{T-1}(S_{1})-V_{T-1}(S_{F}))$
➁the update term of $S_{1}$ when transiting from $S_{F}$ to $S_{1}$:
$\triangle V_{T+1}(S_{1})$
=$\triangle V_{T}(S_{1})$+$laerning\;rate\cdot e(S_{1})\cdot\triangle V_{T}(S_{F})$
=$\alpha\cdot(r_{1}+\gamma\cdot r_{2}+\gamma^{2}\cdot r_{3}+\gamma^{3}\cdot V_{T-1}(S_{F})-V_{T-1}(S_{1}))$
$\;\;+\alpha\cdot\gamma^{3}\cdot(r_{1}’$+$\gamma\cdot V_{T-1}(S_{1})-V_{T-1}(S_{F}))$; where the $\triangle V_{T+1}(S_{1})$ term is the initial temporal difference of $S_{1}$ in the beginning of eposide $T+1$, while $\triangle V_{T}(S_{1})$=$0$ is the initial update term in the beginning of eposide $T$, if we treat eposide $T$ the very first eposide in this case of repeated states.
➂the update term of $S_{1}$ when transiting from $S_{F}$ to $S_{1}$, in the eposide $T$ to $T+1$(the very 1st repeat) could be:
$\alpha\cdot(r_{1}+\gamma\cdot r_{2}+\gamma^{2}\cdot r_{3}+\gamma^{3}\cdot r_{1}’-V_{T-1}(S_{1})\cdot(1-\gamma^{4}))\cdot\gamma^{0}$
, then in the eposide $T+n-1$ to $T+n$(the n-th repeat) could becomes:
$\alpha\cdot(r_{1}+\gamma\cdot r_{2}+\gamma^{2}\cdot r_{3}+\gamma^{3}\cdot r_{1}’-V_{T+n-2}(S_{1})\cdot(1-\gamma^{4}))\cdot\gamma^{n-1}$
, this says in the n-th repeat, the update term of $S_{1}$ in this example should be:
$\alpha\cdot(r_{1}+\gamma\cdot r_{2}+\gamma^{2}\cdot r_{3}+\gamma^{3}\cdot r_{1}’-V_{T+n-2}(S_{1})\cdot(1-\gamma^{4}))\cdot\gamma^{n-1}$From above deduction, we can say that the repeated state influence on temporal difference depends on how far it is to be repeated, that is how many state changes in between the repeated state, the longer the smaller the impact it is!!
Also, the number of times the trajectory has been repeated is a factor expressed in term of $\gamma$ with the exponent of this number minus 1.
[The repeated update term of $S_{2}$::mjtsai1974]I’d like to generalize the expression of update term of $S_{2}$ in the repeated case. Below exhibits the eligibility upgrade in the 1st repeation of $S_{2}$.
Next to investigate the update term of $S_{2}$, the initial temporal difference of $S_{2}$ in eposide $T+1$ consists of below 3 parts:
➀$\alpha\cdot(r_{2}$+$\gamma\cdot r_{3}$+$\gamma^{2}\cdot V_{T-1}(S_{F})-V_{T-1}(S_2))$
This is the part of update term of $S_{2}$ after transiting to $S_{F}$, in eposide $T$.
➁$\alpha\cdot\gamma^{2}\cdot(r_{1}’+\gamma\cdot V_{T-1}(S_{1})-V_{T-1}(S_{F}))$
This is the part of update term of $S_{2}$ contributed from $S_{F}$ to $S_{1}$, be noted that the eligibility of $S_{2}$ is $\gamma^{2}$ at this moment in eposide $T$.
➂$\alpha\cdot\gamma^{3}\cdot(r_{1}+\gamma\cdot V_{T}(S_{2})-V_{T}(S_{1}))$
This is the part of update term of $S_{2}$ contributed when transiting from $S_{1}$ to $S_{2}$ in eposide, watch out, it’s $T+1$ now, thus, we use $V_{T}(S_{1})$, $V_{T}(S_{2})$. The eligibility of $S_{2}$ at this moment is $\gamma^{3}$.Next to add up ➀,➁,➂, we get this expression:
$\triangle V_{T+1}(S_{2})$
=$\alpha\cdot(r_{2}+\gamma\cdot r_{3}+\gamma^{2}\cdot r_{1}’+\gamma^{3}\cdot r_{1}$
$\;\;$+$\gamma^{4}\cdot V_{T}(S_{2})-V_{T-1}(S_{2})$
$\;\;$+$\gamma^{3}\cdot V_{T-1}(S_{1})-\gamma^{3}\cdot V_{T}(S_{1}))$…[A]Can we treat $\gamma\cdot V_{T}(S_{2})\approx V_{T-1}(S_{2})$? Suppose we'd like to decay in a linear, gentle fashion, and $\gamma\rightarrow 1$, after a period of some horizon, the value of a state would just converge, therefore, above expression becomes:
$\alpha\cdot(r_{2}+\gamma\cdot r_{3}+\gamma^{2}\cdot r_{1}’+\gamma^{3}\cdot r_{1}$
$\;\;$-$V_{T-1}(S_{2})(1-\gamma^{3})$
$\;\;$+$\gamma^{3}\cdot (V_{T-1}(S_{1})-V_{T}(S_{1})))$
, where $V_{T-1}(S_{1})\rightarrow V_{T}(S_{1})$ after some period of time, $V_{T-1}(S_{1})-V_{T}(S_{1})\approx 0$ is reasonable, this term could be safely tossed out.However, we are talking about the initial temporal difference of $S_2$ in eposide $T+1$, we should evaluate on the value of $S_{2}$ in eposide $T$. Therefore, back to [A], this time, we choose $V_{T}(S_{2})\approx V_{T-1}(S_{2})$, this holds for convergence. The whole equation becomes:
$\alpha\cdot(r_{2}+\gamma\cdot r_{3}+\gamma^{2}\cdot r_{1}’+\gamma^{3}\cdot r_{1}$
$\;\;$-$V_{T}(S_{2})(1-\gamma^{4}))$It is just the update term of $S_{2}$, $\triangle V_{T+1}(S_{2})$ after its 1st repeat, the same manner as it is in $S_{1}$!!
This says in the n-th repeat, the update term of $S_{2}$ in this example should be:
[The formal expression of the update term in repeated case::mjtsai1974]
$\alpha\cdot(r_{2}+\gamma\cdot r_{3}+\gamma^{2}\cdot r_{1}’+\gamma^{3}\cdot r_{1}$
$\;\;$-$V_{T+n-1}(S_{2})(1-\gamma^{4}))\cdot\gamma^{n-1}$Here, I’d like to make this claim, for the trajectory containing states $\{S_{1}$,$S_{2}$,…,$S_{k}\}$ with the repeated path from $S_{k}$ to $S_{1}$, the update term of $S_{i1}$ in the n-th repeat could be generalized in below expression:
[Cautions]
$\alpha\cdot(r_{i1}+\gamma\cdot r_{i2}+\gamma^{2}\cdot r_{i3}$
+$…+\gamma^{k-1}\cdot r_{ik}-V_{T+n-1}(S_{i1}))\cdot \gamma^{n-1}$, where
$(i1,i2,…,ik)$
=$\{(1,2,3,…,k),$
$\;(2,3,…,k-1,k,1),$
$\;(3,4,…,k,1,2),$
…
$(k,1,2,…,k-2,k-1)\}$Cautions must be made that there exists some other alternative for the deduction of update term expression in repeated case, to be conti in the incoming future.