Model-Based RL Algorithm RMAX - Part 1

08 Feb 2020

Prologue To Model-Based RL Algorithm RMAX - Part 1

RMAX is a simple model-based reinforcement learning algorithm that can attain near-optimal average reward in polynomial time.

MDP Model Construct From Given Data

[Question]

Here is the condition, suppose you are given:
➀a sample of probabilistic transitions and immediate rewards pertaining to a MDP model
➁the full set of states is known in advance
➂but, only the contour, exclusive of the path in between states
➃all states are initialized as unknown

We don’t have the whole MDP yet, what would you do to construct a complete MDP model? What do we do along the way?

[Answer]

We would be able to refer to the Temporal Difference Learning - Part 1, Temporal Difference Learning - Part 2, Temporal Difference In Q Form in my prior post, which is a model-free algorithm.

However, we are given the full set of states, the suggestion would be made to use the RMAX, which is a model-based algorithm.

Before We Enter RMAX Algorithm

[1] Brief description

The approach used by RMAX has been refered to as the optimism in the face of uncertainty heuristic. It propose a specific approach in which the choice in between exploration and exploitation is implicit.

The major insight behind this algorithm is the optimal policy with respect to the agent’s fictitious model has a very interesting and useful property that it is always optimal or it leads to efficient learning.

[2] Preliminaries

The RMAX algorithm was presented in the context of a model called stochastic game in R-max: A General Polynomial Time Algorithm for Near-Optimal Reinforcement Learning, Ronen I. Brafman, CS in Ben-Gurion University, Moshe Tennenholtz, CS in Stanford University. Stochastic game is more general than MDP, because it doesn't necessarily assume that the environment is stochastic.

Please recall in MDP, the execution of the action might not go as well as it has been expected, it is a stochastic environment.

A stochastic game is a model of multi-agent interaction. It has a set of players, each of whom chooses some action to perform from within a given set of actions. As a result of the combinatory choices, some outcome is obtained and is described numerically in the form of a payoff vector, vector of values, one for each of the players.

The RMAX was developed on 2 palyers, fixed-sum games, in which the sum of values in the payoff vector is constant. The player under our control is called the agent, whereas the other one is the adversary.

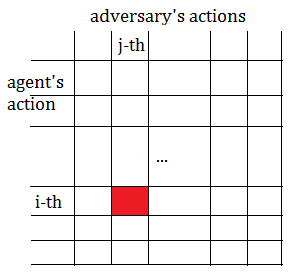
The game is commonly described in strategic form of matrix, the rows of a matrix correspond to the agent’t actions and the columns correspond to the adversary’s actions. The entry of row i and column j contains the rewards obtained for the agent chooses i-th and the adversary chooses the j-th action.

In stochastic game, the player plays a sequence of standard games, which represents the states in normal MDP. After playing a game, it obtains rewards and transits to a new game(or maybe stay in the same place), in both models, actions lead to transitions between states, such similarity could be found.

You could treat MDP as an stochastic game in which the adversary has only a single action at each state.

The RMAX Algorithm

[Input]

Below are the basic defines:
➀$N$: the number of stage games(or states).
➁$k$: the number of actions for each state.
➂$\varepsilon$: the error bound.
➃$\delta$: the algorithm’s failure probability.
➄$R_{max}$: the upper bound on the reward function.
➅$T$: the maximum number of steps for the optimal policy of the algorithm to get $\varepsilon$ close to the average expected(undiscounted) reward.

[Inintialize]

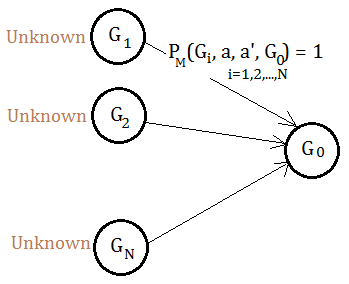
Initialize by constructing a model $M^{'}$ consisting of
➀$N+1$ stage games, ${G_{0},G_{1},…,G_{N+1}}$, corresponding to the real states.
➁$k$ actions, ${a_{1},…,a_{k}}$, which would then be played by the agent and the adversary.
➂set each $G_{i}$ in unknown status.

Where the $G_{0}$ is an additional fictitious game, of which we are in need to initialize the probability for each $G_{i}$ to transite to $G_{0}$ by the agent choosing action $a$ and the adversary choosing $a^{'}$ to be $1$, that is $P_{M}(G_{i},G_{0},a,a^{'})$=$1$, $i$=${0,1,…,N}$.

Cautions must be made that the RMAX Algorithm is using the constructed model $M^{'}$ to approximate the real model $M$, that’s why it is $P_{M}(G_{i},G_{0},a,a^{'})$, not $P_{M^{'}}(G_{i},G_{0},a,a^{'})$.

[Repeat]

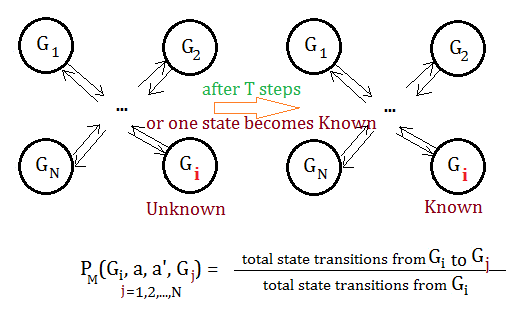
• Compute an optimal $T$-step policy and take action:
  ➀execute this policy for $T$-steps.
  ➁or until a new entry of $G_{i}$ becomes known.

• Keep track of action execution results:
  ➀update the reward thus obtained upon state transition from $G_{i}$ to $G_{j}$ after the execution of joint action of actions $a$ and $a^{'}$ for its very first time.
  ➁update the set of states thus reached in accordance to each action pair $(a,a^{'})$ in $G_{i}$.
  ➂if this entry of $G_{i}$ has been explored over $K_{1}$ times, in other words, the set of states reached from this $G_{i}$ contains $K_{1}$ elements, mark this $G_{i}$ as known, and update the transition probabilities in the unit of distinct transition from $G_{i}$ to $G_{j}$.

Where $K_{1}$=$max((\frac {4\cdot N\cdot T\cdot R_{max}}{\varepsilon})^{3},-6\cdot ln^{3}(\frac {\delta}{6\cdot N\cdot k^{2}}))+1$, which would then be proved in the following secction.

[Brief summary]

The RMAX algorithm constructs a model $M^{'}$ to approximate the real model $M$, by initializing all states as unknown and the probability for each $G_{i}$ of all action pairs $(a,a^{'})$ to $G_{0}$ be $1$.

Based on model $M^{'}$, compute an optimal $T$-step policy, follow from the departuring state in each eposide, say $G_{i}$, keep record of all states reached in accordance to the execution of action pairs $(a, a^{'})$.

At the moment $T$ steps has been reached or the departuring $G_{i}$ turns into known, update the probabilistic transition from this state to its next states. Each time, after such $G_{i}$ has been updated, recompute an optimal $T$-step policy and repeat.

Addendum

➀Exploring Deterministics MDP, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
➁R-max: A General Polynomial Time Algorithm for Near-Optimal Reinforcement Learning, Ronen I. Brafman, CS in Ben-Gurion University, Moshe Tennenholtz, CS in Stanford University