Model-Based RL Algorithm RMAX - Part 3

28 Feb 2020

Prologue To Model-Based RL Algorithm RMAX - Part 3

The major insight behind the RMAX algorithm is the property that it is always either optimal or it leads to efficient learning.

The RMAX Property: Implicit Explore Or Exploit

At each point during the learning process, the agent can either choose one of below:
➀to exoplore to other states, or
➁to exploit over the same state.

If the agent follows an optimal policy with respect to the model it maintains for $T$ steps, it will either attain near-optimal average reward or it will update the statistics for one of the unknown states with sufficient high probability.

The choice in between exploration and exploitation is implicit.

Prerequisites For Implicit Explore Or Exploit

[1] Basic definition

Before we prove the choice in between exploration and exploitation is implicit, there shall exist definition of prerequisites to make this theorem of property more concrete:
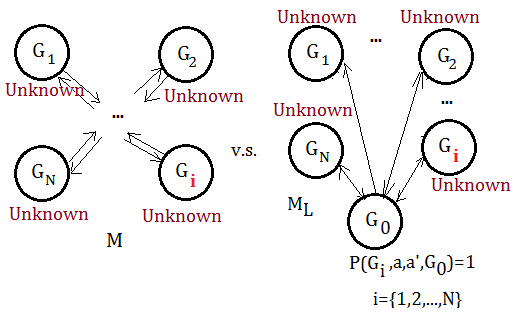
➀define $M$ to be a stochastic game.
➁define $L$ to be a set of unknown states in the form of $(G_{i},a,a^{'})$, that is to say $G_{i}$ is an unknown state.
➂define $M_{L}$ to be a stochastic game identical to $M$, except that $M_{L}$ contains an extra $G_{0}$ state with $P(G_{i},a,a^{'},G_{0})$=$1$ for any $G_{i}\in L$, and the reward is $R_{max}$ for the agent, and $0$ for the adversary.

[2] More detail

Take a more close look in above definition:

• $M_{L}$ is the deduced model of $M$

  ➀in the beginning of RMAX algorithm, we treat all states as unknown.

• After explore or exploit over some horizon in the given sampling of data:
  ➀the reward of known states in $M_{L}$ is at least as large as in $M$, in the instance of $G_{K}$.
  ➁the optimal policy deduced out in $M_{L}$ is also optimal with respect to $M$, could be applied onto $M$. Because $M_{L}$ is almost the same as $M$, except that $M_{L}$ has an extra $G_{0}$ with transitive probability to $1$ from all other states to $G_{0}$.

Base on all above, we’d like to prove the nature of implicit or explicit explore will either attains optimal reward or leads to efficient learning.

Implicit Explore Or Exploit Lemma

Construct the scenario by below list conditions:
➀let $M$ and $M_{L}$ be the same models described above
➁let $\rho$ be any arbitrary policy of the adversary
➂let $0<\alpha<1$
➃let $s$ be any state

When you deduce out an optimal policy $R_{-max}^{ML}$ on the simulated model $M_{L}$ and apply it on the target model $M$, you will either have one of below holds:
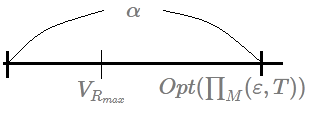
➀$V_{R_{max}}>Opt(\prod_{M}(\varepsilon,T))-\alpha$, where $V_{R_{max}}$ is just the expected $T$-step average reward for $R_{-max}^{ML}$ applied on $M$
➁an unknown entry will be played in the course of running $R_{-max}^{ML}$ on $M$ for $T$ steps with the probability of at least $\frac {\alpha}{R_{max}}$

Such deduced out policy $R_{-max}^{ML}$ on $M_{L}$ is the RMAX policy!!

proof::mjtsai1974

Below illustrates the majority of the lemma:

[1]Begin from the difference in between $V_{R_{max}}$ and $Opt(\prod_{M}(\varepsilon,T))$

➀by artificial design we’d like to have our expected average reward after the execution of RMAX to be greater than the optimal reward of the optimal policy minus $\alpha$, because that would be a little more close to the optimal policy’s reward.

➁$\vert U_{M}(\varepsilon,R_{-max}^{M_{L}},s,T)-U_{M}(\varepsilon,\pi,s,T)\vert$
=$\vert\sum_{q}P(q)\cdot V_{M}(R_{-max}^{M_{L}},q)+\sum_{r}P(r)\cdot V_{M}(R_{-max}^{M_{L}},r)$
$-\sum_{q}P(q)\cdot V_{M}(\pi,q)-\sum_{r}P(r)\cdot V_{M}(\pi,r)\vert$
$\leq\vert\sum_{q}P(q)\cdot V_{M}(R_{-max}^{M_{L}},q)-\sum_{q}P(q)\cdot V_{M}(\pi,q)\vert$
$\;\;$+$\vert\sum_{r}P(r)\cdot V_{M}(R_{-max}^{M_{L}},r)-\sum_{r}P(r)\cdot V_{M}(\pi,r)\vert$

where we have $p$=$\{q,r\}$, $q$ is the path containing all known states, whereas $r$ is the path leads to unknown target/next state.

and $\vert a+b-c-d\vert\leq\vert a-c\vert+\vert b-d\vert$, since $a-c$ might be negative!!

➂due to $q$ is the path to all known states, we have it holds $\vert\sum_{q}P(q)\cdot V_{M}(R_{-max}^{M_{L}},q)-\sum_{q}P(q)\cdot V_{M}(\pi,q)\vert$=$0$

➃the inequality becomes
$\vert U_{M}(\varepsilon,R_{-max}^{ML},s,T)-U_{M}(\varepsilon,\pi,s,T)\vert$
$\leq\vert\sum_{r}P(r)\cdot V_{M}(R_{-max}^{M_{L}},r)-\sum_{r}P(r)\cdot V_{M}(\pi,r)\vert$
$\leq\alpha$
$\leq\sum_{r}P(r)\cdot R_{max}$

and $\alpha\neq 0$, for some $\alpha$ under the condition that $M_{L}\rightarrow_{\alpha}M$, this just holds for $R_{max}$ is just the upper bound for unknown state in RMAX algorithm.

➄then, we have $P(r)\geq\frac {\alpha}{R_{max}}$ just holds

We next to go back to prove the artificial target that the real reward of RMAX is within optimal reward minus something, say $\alpha$.

[2]The real reward of RMAX is within optimal reward minus $\alpha$

➀from above deduction, we already have
$\vert U_{M}(\varepsilon,R_{-max}^{M_{L}},s,T)-U_{M}(\varepsilon,\pi,s,T)\vert\leq\alpha$

➁take off the absolute function, we have below inequality
$U_{M}(\varepsilon,\pi,s,T)-\alpha\leq U_{M}(\varepsilon,R_{-max}^{ML},s,T)\leq U_{M}(\varepsilon,\pi,s,T)+\alpha$

For the left part, it just proves, and we need to step over to the right side.

[3]Step over to the right side

➀since $U_{M_{L}}(\varepsilon,R_{-max}^{M_{L}},s,T)$ is at least as large as $U_{M}(\varepsilon,\pi,s,T)$, see above prerequisites section for detail, therefore it holds
$U_{M}(\varepsilon,\pi,s,T)\leq U_{M_{L}}(\varepsilon,R_{-max}^{M_{L}},s,T)$

➁we have it that
$U_{M}(\varepsilon,R_{-max}^{M_{L}},s,T)\leq U_{M}(\varepsilon,\pi,s,T)+\alpha\leq U_{M_{L}}(\varepsilon,R_{-max}^{M_{L}},s,T)+\alpha$

➂for $R_{-max}^{ML}$ deduced on $M_{L}$, its reward would be at least as large as the optimal policy in $M$, therefore,
$U_{M}(\varepsilon,R_{-max}^{M_{L}},s,T)-\alpha\leq U_{M_{L}}(\varepsilon,R_{-max}^{M_{L}},s,T)$

➃well, we have the deduced out $R_{-max}^{M_{L}}$ on $M_{L}$ is also the optimal policy with respect to $M$, then
$U_{M}(\varepsilon,\pi,s,T)-\alpha\leq U_{M_{L}}(\varepsilon,R_{-max}^{M_{L}},s,T)$

➄as a result that the reward obtained after the execution of $R_{-max}^{M_{L}}$ on $M$ is no less than the reward btained by $R_{-max}^{M_{L}}$ on $M_{L}$, hence
$U_{M}(\varepsilon,\pi,s,T)-\alpha\leq U_{M_{L}}(\varepsilon,R_{-max}^{M_{L}},s,T)\leq U_{M}(\varepsilon,R_{-max}^{M_{L}},s,T)$

We finally go back to the left side of $U_{M}(\varepsilon,\pi,s,T)-\alpha\leq U_{M}(\varepsilon,R_{-max}^{M_{L}},s,T)$ from the righ side.

Addendum

➀R-max: A General Polynomial Time Algorithm for Near-Optimal Reinforcement Learning, Ronen I. Brafman, CS in Ben-Gurion University, Moshe Tennenholtz, CS in Stanford University