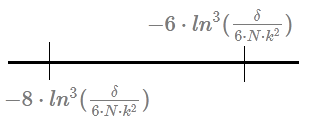Model-Based RL Algorithm RMAX - Part 4
26 Mar 2020Prologue To Model-Based RL Algorithm RMAX - Part 4
The RMAX Theorem
[Theorem of optimality and convergence]Given below condition:
➀let $M$ be the stochastic game with $N$ states and $k$ actions.
➁let $0 < \delta < 1$ and $\varepsilon > 0$ be constants, where $\delta$ is the error probability and $\varepsilon$ is the error term.
➂denote the policy for $M$ whose $\varepsilon$-return mixing time is $T$ by $\prod_{M}(\varepsilon,T)$.
➃denote the optimal expected return by such policy by $Opt(\prod_{M}(\varepsilon,T))$.Then, with probability of no less than $1-\delta$ the RMAX algorithm will attain an expected return of $Opt(\prod_{M}(\varepsilon,T))-2\cdot\varepsilon$, within a number of steps polynomial in $N$,$k$,$T$,$\frac {1}{\varepsilon}$ and $\frac {1}{\delta}$.
Notes::mjtsai1974Why the execution of the RMAX algorithm will attain an expected return of $Opt(\prod_{M}(\varepsilon,T))-2\cdot\varepsilon$?
As a result of the fact that the optimal policy is defined on $\varepsilon$-return mixing time of $T$, the real return of the execution of the RMAX algorithm must be smaller than it, thus we choose it to be $-2\cdot\varepsilon$.
Why the RMAX algorithm is polynomial?
[1] Recap on implicit explore or exploit lemmaThe implicit explore or exploit lemma guarantees that the policy generated from the simulated model $M_{L}$ onto the target model $M$ could either leads to $\alpha$ close to optimal reward or explore efficiently with hight probability of at least $\frac {\alpha}{R_{max}}$, where $M_{L}\rightarrow_{\alpha}M$ and $\alpha$=$\frac {\varepsilon}{N\cdot T\cdot R_{max}}$.
[2] Due to $\alpha$ approximationSince $\alpha$=$\frac {\varepsilon}{N\cdot T\cdot R_{max}}$, the $T$ step phases in which we are exploring in the execution of the RMAX algorithm is polynomial in $N$,$T$,$\varepsilon$.
[3] Learn over $N$ states and $k^{2}$ actionsThere are totally $N$ states(or stage games) in model $M$ with $k$ actions for the agent and the adversary, therefore, we have a polynomial number of parameters to learn, say $N$ and $k$.
[4] The probability to update the unknown informationThe probability the RMAX alrorithm to turn a state from unknown to known or to update statistics information is polynomial in $\varepsilon$,$T$,$N$.
[Notes] A brief summaryBase on all of above, by sampling in a large number of times, the implicit explore or exploit lemma guarantees the least probabilistic exploration, and we can ensure that the fail rate in attaining the optimal reward is quiet small, say $\delta$.
The RMAX algorithm claims that we can get near optimal reward with probability $1-\delta$ by sampling a sufficient large number of trials over the same state, which is polynomial in $\frac {1}{\delta}$.
Watch out that each trial contains either exploration or exploitation, next to prove this theorem.
The RMAX Theorem Proof::1
[1] The accuracy in the estimate of transitive probabilityFirst, we’d like to prove that the estimate of transitive probability in the implicit explore or exploit is accurate.
The majority focus on the number of trials in this same state, that is how many times of state transition in this same state for explore or exploit could we believe that the estimated transitive probability is accurate?
[2] By sampling in a large number of trials over the same state
How many number of trials on $G_{i}$(in this same state) could we update the transitive statistics of $G_{i}$?
➀suppose there exists such transitive probability $p$ on $G_{i}$, it could not be guaranteed with probability $1$, that is $0\leq p\leq 1$.
➁totally, there are $N\cdot k^{2}$ such probabilities, for we have $N$ states, with agent and adversary each having $k$ actions.
➂treat the random variable $X_{i}$ to be the distinct trial on state $G_{i}$, with above denoted transitive probability $p$ to transite from state $G_{i}$ to $G_{i^{'}}$, that is to say
- The value of $X_{i}$=$1$, iff it transits from $G_{i}$ to $G_{i^{'}}$ with probability $p$; otherwise, the value of $X_{i}$=$0$, iff it just revisits over the same state $G_{i}$ with probability $1-p$.
➃let $Z_{i}$=$X_{i}-p$, then
$E\lbrack Z_{i}\rbrack$
=$E\lbrack X_{i}-p\rbrack$
=$E\lbrack X_{i}\rbrack$-$p$
=$1\cdot p$-$p$
=$0$, and $\vert Z_{i}\vert\leq 1$
- By Chernoff Bounds For Bernoulli Random Variable
We have $P(\sum_{i=1}^{n}Z_{i}>a)<e^{-\frac {a^{2}}{2\cdot n}}$, where $Z_{1}$,$Z_{2}$,…,$Z_{n}$ are the $n$ distinct independent trials on state $G_{i}$, and $a$ is the error term, such inequality is to ask for the error probability that after $n$ independent trials on state $G_{i}$, the total estimate bias is greater than the error term $a$. This error probability is upper bounded by $e^{-\frac {a^{2}}{2\cdot n}}$.➄if we perform the test on this state $G_{i}$ for $K_{1}$ times, then we have the inequality holds
$P(\sum_{i=1}^{K_{1}}Z_{i}>K_{1}^{\frac {2}{3}})<e^{-\frac {K_{1}^{\frac {1}{3}}}{2}}$
The RMAX paper would like to restrict the total loss(or bias) in the estimate of transitive probability $p$ on $G_{i}$ over $K_{1}$ times to be less than $K_{1}^{\frac {2}{3}}$ and such error probability is upper bounded by $e^{-\frac {K_{1}^{\frac {1}{3}}}{2}}$.
- Inequality symmetry and regularization
If we take $Z_{i}^{'}$=$p-X_{i}$,
then $P(\sum_{i=1}^{K_{1}}Z_{i}^{'}>K_{1}^{\frac {2}{3}})<e^{-\frac {K_{1}^{\frac {1}{3}}}{2}}$,
therefore, $P(\vert\sum_{i=1}^{K_{1}}(X_{i}-p)\vert>K_{1}^{\frac {2}{3}})<2\cdot e^{-\frac {K_{1}^{\frac {1}{3}}}{2}}$ by symmetry,
finally, $P(\vert\frac {\sum_{i=1}^{K_{1}}X_{i}}{K_{1}}-p\vert>K_{1}^{-\frac {1}{3}})<2\cdot e^{-\frac {K_{1}^{\frac {1}{3}}}{2}}$.➅back to our departuring point that the RMAX algorithm would like to attain/get close to the optimal reward with probability $1-\delta$, where $\delta$ is the error probability.
- To limit the probabilistic failure of the estimated transitive probability
We want this probabilistic failure smaller than $\delta$, in the paper proof, it was upper bounded by $\frac {\delta}{3\cdot N\cdot k^{2}}$, this would be definitely be smaller than $\delta$, by taking $2\cdot e^{-\frac {K_{1}^{\frac {1}{3}}}{2}}<\frac {\delta}{3\cdot N\cdot k^{2}}$.
- To limit the total estimated loss after $K_{1}$ trials
In the paper proof, we choose the error term to be expressed as $K_{1}^{-\frac {1}{3}}<\frac {\varepsilon}{2\cdot N\cdot T\cdot R_{max}}$, then the total estimated loss must be less than $\varepsilon$.
➆expand from $2\cdot e^{-\frac {K_{1}^{\frac {1}{3}}}{2}}<\frac {\delta}{3\cdot N\cdot k^{2}}$
$\Rightarrow K_{1}>-8\cdot ln^{3}(\frac {\delta}{6\cdot N\cdot k^{2}})$
, and we can choose $K_{1}>-6\cdot ln^{3}(\frac {\delta}{6\cdot N\cdot k^{2}})$ to narrow down the interval of probabilistic estimation failure.
➇expand from $K_{1}^{-\frac {1}{3}}<\frac {\varepsilon}{2\cdot N\cdot T\cdot R_{max}}$
$\Rightarrow K_{1}>(\frac {2\cdot N\cdot T\cdot R_{max}}{\varepsilon})^{3}$
, and $K_{1}>(\frac {4\cdot N\cdot T\cdot R_{max}}{\varepsilon})^{3}$ holds for it.Finally, $K_{1}$=$max((\frac {4\cdot N\cdot T\cdot R_{max}}{\varepsilon})^{3},-6\cdot ln^{3}(\frac {\delta}{6\cdot N\cdot k^{2}}))+1$, after this $K_{1}$ trials over the same state, we are confident to to turn a state from unknown to known or to update its statistics information, we believe that the estimated transitive probability is accurate.
The RMAX Theorem Proof::2
The implicit explore or exploit lemma yields a transitive probability of $\frac {\alpha}{R_{max}}$, we next show that after pure exploration over $K_{2}$ trials on this same state $G_{i}$, we can obtain $K_{1}$ required visits on $G_{i}$.
➀let $X_i$ be the random variable of indicator for each trial, whose value is $1$ iff it transits from $G_{i}$ to $G_{i^{'}}$; or $0$ iff it justs exploits in the same $G_{i}$.
➁let $Z_{i}$=$X_{i}-\frac {\alpha}{R_{max}}$ and $Z_{i}^{'}$=$\frac {\alpha}{R_{max}-X_{i}}$, then $E\lbrack Z_{i}\rbrack$=$0$ and $E\lbrack Z_{i}^{'}\rbrack$=$0$ respectively.
- By Chernoff Bounds For Bernoulli Random Variable
$P(\vert\sum_{i=1}^{K_{2}}(X_{i}-\frac {\alpha}{R_{max}})\vert>K_{2}^{\frac {1}{3}})<2\cdot e^{-\frac {K_{2}^{-\frac {1}{3}}}{2}}$
$\Rightarrow P(\vert\sum_{i=1}^{K_{2}}X_{i}-\frac {K_{2}\cdot\alpha}{R_{max}}\vert>K_{2}^{\frac {1}{3}})<2\cdot e^{-\frac {K_{2}^{-\frac {1}{3}}}{2}}$- To limit the error terms
Take $2\cdot e^{-\frac {K_{2}^{-\frac {1}{3}}}{2}}<\frac {\delta}{3\cdot N\cdot k^{2}}$
, and take $\frac {K_{2}\cdot\alpha}{R_max}+K_{2}^{\frac {1}{3}}>K_{1}\cdot N\cdot k^{2}$
, for totally we have $N\cdot k^{2}\cdot K_{1}$ number of visits to unknown slots. These guarantee that the fail probability less than $\frac {\delta}{3}$, which is much smaller than $\delta$.- Why $K_{2}^{\frac {1}{3}}$ as the error term instead of $K_{2}^{\frac {2}{3}}$?
The design of this proof is to find the least $K_{2}$ pure exploration trials, thus guarantees that we could have $K_{1}$ visits on this same state. Since $K_{1}$ contains exploration and exploitation, $K_{2}\leq K_{1}$, therefore, the error term is expressed in terms of $K_{2}^{\frac {1}{3}}$, rather than $K_{2}^{\frac {2}{3}}$!! We want a smaller $K_{2}<K_{1}$ and $K_{2}^{\frac {1}{3}}<K_{1}^{\frac {2}{3}}$.
The RMAX Theorem Proof::3
This section discuss the scenario that we perform $T$-step iterations without learning, that is to say it exploits over $T$ steps, and the optimal expected reward would be $Opt(\prod_{M}(T,\varepsilon))-\varepsilon$.
- The actual return may be lower
Since the actual reward after execution of the RMAX algorithm would be some distance from optimal reward, it is at most $Opt(\prod_{M}(T,\varepsilon))-\varepsilon$, it is lower than $Opt(\prod_{M}(T,\varepsilon))-\varepsilon$, which is plausible. If we prevent it from exploring, we are at least staying in some local suboptimal.
- We want it to be more closer
To align the design in above section, we choose the real return of exploitation after $T$-step iterations to be $Opt(\prod_{M}(T,\varepsilon))-\frac {3}{2}\varepsilon$, then it is $\frac {1}{2}\varepsilon$ close to the optimal reward $Opt(\prod_{M}(T,\varepsilon))-\varepsilon$. The RMAX paper upper bound the failure probability by $\frac {\delta}{3}$.➀take $X_{i}$ to be the actual reward obtained in each trial
➁treat $\mu$ as the optimal reward
➂then by $y_{i}$=$\frac {\mu-X_{i}}{R_{max}}$ could we stablize the standard deviation, since it is bounded by $R_{max}$
➃suppose $Z$=$M\cdot N\cdot T$, where $M>0$, after $Z$ exploitations, the failure probability that the total loss greater than $Z^{\frac {2}{3}}$ is upper bounded by $e^{-\frac {Z^{\frac {1}{3}}}{2}}$
- By Chernoff Bounds For Bernoulli Random Variable
$P(\sum_{i=1}^{Z}Y_{i}>Z^{\frac {2}{3}})<e^{-\frac {Z^{\frac {1}{3}}}{2}}$
$\Rightarrow P(\sum_{i=1}^{Z}\frac {\mu-X_{i}}{R_{max}}>Z^{\frac {2}{3}})<e^{-\frac {Z^{\frac {1}{3}}}{2}}$
$\Rightarrow P(\sum_{i=1}^{Z}\frac {\mu-X_{i}}{Z\cdot R_{max}}>Z^{-\frac {1}{3}})<e^{-\frac {Z^{\frac {1}{3}}}{2}}$
$\Rightarrow P(\sum_{i=1}^{Z}\frac {\mu-X_{i}}{Z}>\frac {R_{max}}{Z^{\frac {1}{3}}})<e^{-\frac {Z^{\frac {1}{3}}}{2}}$➄by choosing $M$ such that
$\frac {R_{max}}{Z^{\frac {1}{3}}}<\frac {\varepsilon}{2}$ and $e^{-\frac {Z^{\frac {1}{3}}}{2}}<\frac {\delta}{3}$
$\Rightarrow Z>(\frac {2\cdot R_Max}{\varepsilon})^{3}$ and $Z>6\cdot ln^{3}(\frac {\delta}{3})$,
We thus have the failure probability less than $\frac {\delta}{3}$ for the real return obtained is $\frac {\varepsilon}{2}$ far away from the optimal reward.