Partial Observable Markov Decision Process - Part 1

21 Jul 2020

Prologue To Partial Observable Markov Decision Process - Part 1

This post is an entry of POMDP(Partial Observable Markov Decision Process), from the most foundamental to the belief update.

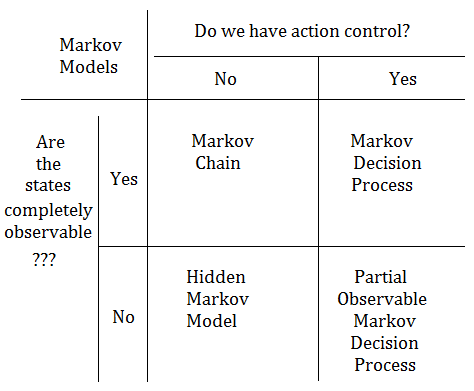
Summary Of All Markov Models

[1] Markov chain

➀finite number of discrete states with probabilistic transition between states.
➁the Makrov property is that next state is determined by current state only!!

[2] Hidden Markov model

➀all the same in Markov chain, except that we're unsure which state we are in.
➁the current state emits an observation.

[3] Markov decision process

➀finite number of discrete states.
➁probabilistic transition between states and executable actions in each state.
➂next state is determined by current state and current action.
➃the execution of an action might lead to unexpected result due to random stochasticity.

[4] Partial observal Markov decision process

➀all the same as Markov decision process, except that we're unsure which state we are in.
➁the current state emits an observation.

Below table exhibits the summary:

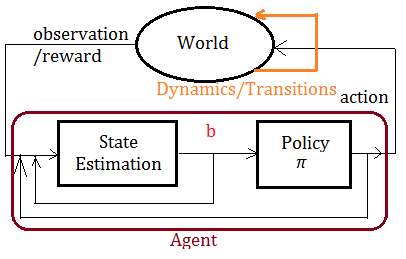
Belief State In POMDP

Below exhibits the POMDP model, wherein the probability distribution is over the world states with true state is only partially observable.

➀the agent keeps/maintains an internal belief state, say $b$, that summarizes its experience.
➁the agent makes state estimation to update from belief state $b$ to next belief state $b^{'}$, based on the last action it has taken, the current observation it has made, and the previous belief state $b$.

[Question]Why Belief State in POMDP?

[Answer]

➀the state of the real world is only partially observable.
➁the agent needs to learn how the observations might aid its performance.
➂there might exists no immediate observation pertaining to the desired state.
$\Rightarrow$This rerveals that the states are probabilistically distributed over the given observations at any time, such probability distribution varies over time, that’s why we have belief state from initial $b$ to $b^{'}$, or say from $b_{0}$ to $b_{1}$, $b_{2}$,…,$b_{i}$, $b_{i+1}$,…,$b_{\infty}$.

➃the whole POMDP is illustrated/iterated in the environment of uncertainty.
➄uncertainty about action outcome, about the world state due to imperfect(partial) information.

POMDP Parameters

➀initial belief:
$b(S)$=$P(S)$, this means the probability for we are in state $S$.
➁belief state updating:
$b^{'}(S^{'})$=$P(S^{'}|O,A,b)$, this represents the probability for we are in state $S^{'}$, given that we take action $A$, make observation $O$, from previous belief state distribution, say $b$.
➂observation function:
$\Omega(S^{'},A,O)$=$P(O|S^{'},A)$, it represents the probability for we make observation $O$, given that we are transiting to state $S^{'}$, by taking action $A$.
➃transitive probability:
$T(S,A,S^{'})$=$P(S^{'}|S,A)$, it represents the probability for we transit from $S$ to $S^{'}$, by taking action $A$.
➄rewards:
$R(A,b)$=$\sum_{S}R(S,A)\cdot b(S)$, where $R(S,A)$ is the same as it is in MDP, and the reward is summing over the reward by taking action $A$ with proportion to the probabilistic distribution for each state $S$ in $b$.

Understand The Belief State $b$

Suppose we are given $n$ underlying states, a discrete state space of size $n$, then the belief state $b$ is a vector of $n$ states.

Partial observable turns discrete problem of $n$ states into continuous problem, a POMDP with $n$ states induces an $n$-dimensional belief-MDP.

• Why?

[Answer]

The true state is only partial observable, where $b(S)$=probability of being in state $S$.
At each step, the agent:
➀takes some action, say $A$
➁transites to next state $S^{'}$ form state $S$
➂makes observation $O$, with probability $P(O|S^{'},A)$
➃suppose we are given initial belief state $b$, after ➀,➁,➂, the probabilistic distribution over the belief state would definitely be changed.

• The posterior belief
  That’s why we need to make belief update, say the posterior belief:
  $b^{'}(S^{'})$=$\alpha\cdot P(O|S^{'},A)\cdot\sum_{S}P(S^{'}|S,A)\cdot b(S)$
  , where $\alpha$ is certain coefficient, such belief update is continuous rather than discrete!!!

• Continuous belief update

  POMDP could be regarded as continuous belief update over underlying MDP states, as the agent’s belief is encoded through a continuous belief state.
  Each MDP state is a probability distribution(continuous belief state) over the state of the original POMDP.

POMDP: Belief Update

$b^{'}(S^{'})$
=$P(S^{'}|A,O,b)$, we believe we are in state $S^{'}$, given observation $O$
=$P(O|S^{'},A,b)\cdot\frac {P(S^{'}|A,b)}{P(O|A,b)}$

mjtsai think we can treat $b'(S')$ as $P(S'|O)$ in viewpoint of Bayer theorem.

• $P(O|S^{'},A,b)$
  ➀it is the probability that we make observation $O$, given that we are in state $S^{'}$, by taking action $A$, probabilistically distributed over belief state $b$(or say from previous belief state $b$).
  ➁therefore, we can treat $P(O|S^{'},A,b)$=$P(O|S^{'})$

• $P(S^{'}|A,b)$
  This stands for the probability that we are in $S^{'}$, given action $A$ has been taken, from belief state $b$
  , where $P(S^{'}|A,b)$=$\sum_{S}P(S^{'}|A,S)\cdot b(S)$ and this $b$ is to be believed a vector of states, a vector of state space.

• $P(O|A,b)$
  This indicates we make observation $O$, given that we has taken action $A$, from belief state $b$
  , this is a normalization factor, where
  $P(O|A,b)$
  =$\sum_{S^{''}}P(O|S^{''})\cdot P(S^{''}|A,b)$
  =$\sum_{S^{''}}P(O|S^{''})\cdot\sum_{S}P(S^{''}|A,S)\cdot b(S)$

Notes::mjtsai1974

This expression is asking for the probability of the fact that we are in state $S^{'}$, given that we make observation $O$, by taking action $A$, from somewhat belief state $b$.

It could be further expanded as the qualitative probability that we make observation $O$, given that we are in state $S^{'}$, by taking action $A$, from belief state $b$. Such likeli in turn multiplied by the probabilty, which is a prior that we are in $S^{'}$, by taking action $A$, from belief state $b$. Finally, over the total/marginal probability probability that we make observation $O$, given that we take action $A$, from somewhat belief state $b$.

Addendum

➀Partial Observable Markov Decision Process, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
➁Partially Observable Markov Decision Process, Geoff Hollinger, 2007 fall
➂Prof. Dr.-Ing. Stefan Kopp, 2010, Bielefed University