23 Apr 2018
Prologue To The Poisson Process Inter-arrival Times
On the way to the Poisson distribution, the inter-arrival times could be easily found, and both exponential and Poisson distribution could be an appropriate modeling of it. Formally, inter-arrival times could be distributed in gamma probability as a result of the nature of exponential distribution.
The Inter-arrival Times
Given that $X_{1}$,$X_{2}$,…,$X_{n}$ are random variables with event outcome occurrences arrived at specific time. To make it more formally, we take the difference $T_{i}$=$X_{i}$-$X_{i-1}$ as the inter-arrival times.
The Very First Inter-arrival Times Follows Exponential Distribution
We start to derive the probability distribution of inter-arrival times, let’s focus on the very first one as the prelude.
➀take $T_{1}$=$X_{1}$ as the very first arrival time.
➁the probability of first arrival at time greater than t is equivalent to the probability of zero arrival within time $[0,t]$.
$P(T_{1}\le t)$
=1-$P(T_{1}>t)$=1-$P(N_{[0,t]}=0)$=1-$e^{-\lambda\cdot t}$
, where $\lambda$ is the intensity, the rate of event occurrence.
The very first inter-arrival times is itself an exponential distribution.
The Distribution Of Distinct Inter-arrival Times
If you take a close look at the random arrivals over the horizon, trivially, numerous distinct inter-arrival times could be found.
Suppose you are given two adjacent inter-arrival times, $T_{i}$=$s$,$T_{i+1}$=$t$. We are asking the probability for we have the second arrival after time duration $t$, under the condition that we have the first arrival with regards to $T_{i}$=$s$.
This turns into the conditional probability.
$P(T_{i+1}>t|T_{i}=s)$
=$P(T_{i+1}>t,T_{i}=s|T_{i}=s)$
=$P(N_{(s,s+t]}=0,N_{[0,s]}=1|N_{[0,s]}=1)$
=$\frac {P(N_{(s,s+t]}=0\cap N_{[0,s]}=1)}{P(N_{[0,s]}=1)}$
=$\frac {P(N_{(s,s+t]}=0)\cdot P(N_{[0,s]}=1)}{P(N_{[0,s]}=1)}$…independence
=$P(N_{(s,s+t]}=0)$
=$e^{-\lambda\cdot(t)}$
Therefore, $P(T_{i+1}\le t|T_{i}=s)$=1-$P(T_{i+1}>t|T_{i}=s)$=1-$e^{-\lambda\cdot(t)}$
We can claim that each distinct inter-arrival times has an exponential distribution. Some textbook treat it as the one-dimensional Poisson process.
The Joint Distribution Of Random Arrivals::mjtsai1974
Due to the nature of the exponential distribution, we can then derive the joint distribution of numerous random arrivals in the unit of each distinct inter-arrival times as a whole.
By one-dimensional Poisson process, we know that all $T_{i}$’s are independent and each has an $Exp(\lambda\cdot t)$ distribution, where $t$ is the inter-arrival times. Let me state below claim:
➀$T_{i}$=$X_{i}$-$X_{i-1}$
➁$X_{i}$=$T_{i}$+$T_{i-1}$
➂where ➀,➁is the rule for each new arrival, $T_{0}$=$X_{0}$=$0$ by default.
Then, $F_{T_{i}}$=$P(T_{i}\le t)$=1-$e^{-\lambda\cdot t}$, for $i$=$1$,$2$,$3$,…
I’d like to prove that the joint distribution of random arrivals is just a gamma distribution.
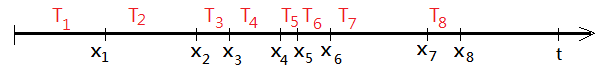
proof::mjtsai1974
[1]begin by time tick at $0$, say we use $X_{1}$ as the random variable to represent the first one arrival within whatever time length $t$ is, denote time period $[0,t]$ as $T_{1}$.
➀$F_{X_{1}}(t)$=$F_{T_{1}+T_{0}}(t)$=$P(T_{1}\le t)$=1-$e^{-\lambda\cdot t}$, where $T_{0}$=$0$
➁$f_{X_{1}}(t)$=$\lambda\cdot e^{-\lambda\cdot t}$
Trivially, by previous section, each $X_{i}$ just has an exponential distribution.
[2]for whatever $T_{1}$ is, after that, say we’d like to have the second arrival within time length $t$, and use the $X_{2}$ as the random variable for the second arrival.
➀$T_{2}$=$X_{2}$-$X_{1}$ and $X_{2}$=$T_{2}$+$T_{1}$
➁$F_{X_{2}}(t)$
=$F_{T_{2}+T_{1}}(t)$
=$P(T_{2}+T_{1}\le t)$…take $Y$=$T_{1}$,$X$=$T_{2}$
=$\int_{0}^{t}\int_{0}^{t-y}f_{X}(x)\cdot f_{Y}(y)\operatorname dx\operatorname dy$
=$\int_{0}^{t}F_{X}(t-y)\cdot f_{Y}(y)\operatorname dy$
➂differentiate $F_{X_{2}}(t)$ with respect to its current variable, say $t$.
$f_{X_{2}}(t)$
=$\int_{0}^{t}f_{X}(t-y)\cdot f_{Y}(y)\operatorname dy$
=$\int_{0}^{t}\lambda\cdot e^{-\lambda\cdot(t-y)}\cdot\lambda\cdot e^{-\lambda\cdot y}\operatorname dy$
=$\lambda^{2}\cdot e^{-\lambda\cdot t}\int_{0}^{t}\operatorname dy$
=$\lambda^{2}\cdot t\cdot e^{-\lambda\cdot t}$
If you set $X$=$T_{1}$,$Y$=$T_{2}$ in deduction, still the same result you can get.
[3]for whatever $T_{2}$ is, after that, we use the $X_{3}$ as the random variable for the third arrival, and would like to have it within time length $t$.
➀$X_{3}$=$T_{3}$+$T_{2}$+$T_{1}$
➁$F_{X_{3}}(t)$
=$F_{T_{3}+T_{2}+T_{1}}(t)$
=$P(T_{3}+T_{2}+T_{1}\le t)$…take $Y$=$T_{2}$+$T_{1}$,$X$=$T_{3}$
=$\int_{0}^{t}\int_{0}^{t-y}f_{X}(x)\cdot f_{Y}(y)\operatorname dx\operatorname dy$
=$\int_{0}^{t}F_{X}(t-y)\cdot f_{Y}(y)\operatorname dy$
➂differentiate $F_{X_{3}}(t)$ with respect to its current variable, say $t$.
$f_{X_{3}}(t)$
=$\int_{0}^{t}f_{X}(t-y)\cdot f_{Y}(y)\operatorname dy$
=$\int_{0}^{t}\lambda\cdot e^{-\lambda\cdot(t-y)}\cdot(\lambda)^{2}\cdot y\cdot e^{-\lambda\cdot y}\operatorname dy$
=$\lambda^{3}\cdot e^{-\lambda\cdot t}\int_{0}^{t}y\operatorname dy$
=$\frac {1}{2}\cdot\lambda^{3}\cdot t^{2}\cdot e^{-\lambda\cdot t}$
If you set $X$=$T_{2}$+$T_{1}$,$Y$=$T_{3}$ in deduction, still the same result you can get.
[4]repeat above procedure until $n\rightarrow\infty$, we will have $F_{X_{n}}(t)$ holds to have its derivative $f_{X_{n}}(t)$=$\frac {\lambda\cdot(\lambda\cdot t)^{n-1}\cdot e^{-\lambda\cdot t}}{(n-1)!}$, for $n$=$1$,$2$,…, where $\Gamma(n)$=$(n-1)!$.
[5]by means of mathematics induction, we can conclude that the joint distribution of random arrivals is just a gamma distribution. Be recalled that $f_{X_{n}}(t)$=$\frac {\lambda\cdot(\lambda\cdot t)^{n-1}\cdot e^{-\lambda\cdot t}}{(n-1)!}$ is a gamma probability function in Introduction To The Gamma Distribution.
Example: Illustrate The Poisson Probability For Points Distribution
Suppose you are given $n$ points randomly generated within an interval, how to evaluate the points location? Just treat the inter-arrival times as the location info, it suffice to evaluate the probability of points arrival by means of Poisson distribution.
Let’s say the interval is $[0,a]$, explore one arrival case within this interval as a beginning.
[1]assume $0<s<a$, we now know one arrival occurred within $[0,a]$, the probability of this one arrival occurrence within $s$, under the condition that this occurrence is within $[0,a]$:
$P(X_{1}\le s|N_{[0,a]}=1)$
=$P(X_{1}\le s,N_{[0,a]}=1|N_{[0,a]}=1)$
=$P(N_{(0,s]}=1,N_{[0,a]}=1|N_{[0,a]}=1)$
=$P(N_{(0,s]}=1,N_{[s,a]}=0|N_{[0,a]}=1)$
=$\frac {\lambda\cdot s\cdot e^{-\lambda\cdot s}\cdot e^{-\lambda\cdot(a-s)}}{\lambda\cdot a\cdot e^{-\lambda\cdot a}}$
=$\frac {s}{a}$
$X_{1}$ is uniformly distributed within $[0,a]$
, given the event ${N_{[0,a]}=1}$ as the condition, since $\sum_{i=1}^{s}\frac {1}{a}$=$\frac {s}{a}$.
[2]suppose that there are two arrivals in $[0,a]$, that is $N_{[0,a]}=2$, and given $0<s<t<a$, we can show $P(X_{1}\le s,X_{2}\le t|N_{[0,a]}=2)$=$\frac {t^{2}-(t-s)^{2}}{a^{2}}$.
proof::mjtsai1974
➀this is to ask out the probability that first arrival falls within $[0,s]$, the second arrival falls within $(s,t]$. Below graph exhibits the possible cases.
 ➁by above table, we just need to accumulate the probability of the case (1) and (2), which is equivalent to substract the probability of two event occurrences in $(s,t]$ from the probability that two event arrivals in $[0,t]$.
➁by above table, we just need to accumulate the probability of the case (1) and (2), which is equivalent to substract the probability of two event occurrences in $(s,t]$ from the probability that two event arrivals in $[0,t]$.
$P(X_{1}\le s,X_{2}\le t|N_{[0,a]}=2)$
=$\frac {P(X_{1}\le s,X_{2}\le t\cap N_{[0,a]}=2)}{P(N_{[0,a]}=2)}$
=$\frac {P(X_{1},X_{2}\le t)-P(s<X_{1},X_{2}\le t)}{P(N_{[0,a]}=2)}$
=$\frac {P(N_{[0,t]}=2)\cdot P(N_{(t,a]}=0)-P(N_{[0,s)}=0)\cdot P(N_{[s,t]}=2)\cdot P(N_{(t,a]}=0)}{P(N_{[0,a]}=2)}$
=$\frac {\frac {(\lambda\cdot t)^{2}}{2!}\cdot e^{-\lambda\cdot t}\cdot\frac {(\lambda\cdot(a-t))^{0}}{0!}\cdot e^{-\lambda\cdot(a-t)}-\frac {(\lambda\cdot s)^{0}}{0!}\cdot e^{-\lambda\cdot s}\cdot\frac {(\lambda\cdot(t-s))^{2}}{2!}\cdot e^{-\lambda\cdot(t-s)}\cdot\frac {(\lambda\cdot(a-t))^{0}}{0!}\cdot e^{-\lambda\cdot(a-t)}}{\frac {(\lambda\cdot a)^{2}}{2!}\cdot e^{-\lambda\cdot a}}$
=$\frac {\frac {(\lambda\cdot t)^{2}}{2!}\cdot e^{-\lambda\cdot t}-\frac {(\lambda\cdot(t-s))^{2}}{2!}\cdot e^{-\lambda\cdot(t-s)-\lambda\cdot s-\lambda\cdot(a-t)}}{\frac {(\lambda\cdot a)^{2}}{2!}\cdot e^{-\lambda\cdot a}}$
=$\frac {\frac {(\lambda\cdot t)^{2}}{2!}\cdot e^{-\lambda\cdot t}-\frac {(\lambda\cdot(t-s))^{2}}{2!}\cdot e^{-\lambda\cdot a}}{\frac {(\lambda\cdot a)^{2}}{2!}\cdot e^{-\lambda\cdot a}}$
=$\frac {t^{2}-(t-s)^{2}}{a^{2}}$
Cautions must be made that the event order just matters.
➂$P(X_{1}\le s,X_{2}\le t|N_{[0,a]}=2)$
=$\frac {t^{2}-(t-s)^{2}}{a^{2}}$
=$\frac {t-(t-s)}{a}\cdot\frac {t+(t-s)}{a}$
=$\frac {s}{a}\cdot\frac {t+(t-s)}{a}$
=$\frac {s}{a}\cdot\frac {t}{a}$+$\frac {s}{a}\cdot\frac {(t-s)}{a}$
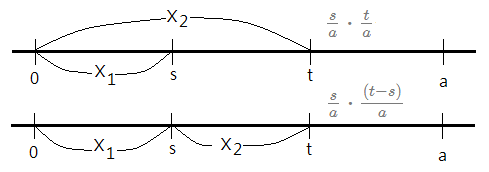
$X_{1}$,$X_{2}$ are uniformly distributed within $[0,a]$
, given the event ${N_{[0,a]}=2}$ as the condition.
Therefore, we can claim that the Poisson process has $n$ random arrivals in time inteerval $[a,b]$, the locations of these points are independent distributed, and each of them has a uniform distribution.
22 Apr 2018
Prologue To The Poisson Distribution
In probability theory and statistics, the Poisson distribution is the process developed with a hope to approximate the scenario of random arrival within a given time period.
The random variable of the interarrival time modeled by the Poisson process is identical to the result deduced out by the exponential distribution, we could also express the interarrival time as kind of a special case of gamma distribution.
The Poisson Process Illustration
The Poisson process is a simple kind of random process, describing random points distribution in time or space. It is developedn based on be low two assumptions:
[1]homogeneity: it assumes the rate $\lambda$ of event occurrence is constant over time. The expected unmber of random point arrivals over time period $t$ is $\lambda\cdot t$.
[2]independence: it assumes all random occurrences are independent. This says that the number of arrivals over disjoint time intervals are independent random variables.
Next the illustration of the procerss.
➀suppose within a time interval $[0,t]$, the arrival of points or the occurrence of events are random and is represented by random variables $X_{1}$, $X_{2}$, $X_{3}$…, and this scenario is compliants with homogeneity and independence.
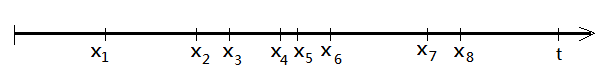 This article denotes the total number of occurrences within $[0,t]$ as $N([0,t])$, or just abbreviating $N_{t}$ for over time length $t$. The homogeneity implies that $E\lbrack N_{t}\rbrack$=$\lambda\cdot t$.
This article denotes the total number of occurrences within $[0,t]$ as $N([0,t])$, or just abbreviating $N_{t}$ for over time length $t$. The homogeneity implies that $E\lbrack N_{t}\rbrack$=$\lambda\cdot t$.
➁to be more precisely approximate to the distribution of such random arrivals, we divide the time period $t$ by $n$, to be believed that $n$ is large enough.
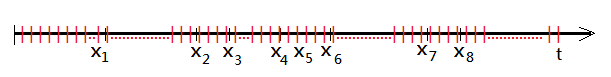 Then we have each distinct subinterval of time length $\frac {1}{n}$, and each subinterval would just have success of $1$ arrival, or failure of $0$ arrival, which itself is a Bernoulli distribution.
Then we have each distinct subinterval of time length $\frac {1}{n}$, and each subinterval would just have success of $1$ arrival, or failure of $0$ arrival, which itself is a Bernoulli distribution.
➂each subinterval has time length $\frac {t}{n}$, the $i$-th subinterval ranges from time $\frac {(i-1)\cdot t}{n}$ to $\frac {i\cdot t}{n}$. We take $R_{i}$ as the $i$-th event in each distinct subinterval.
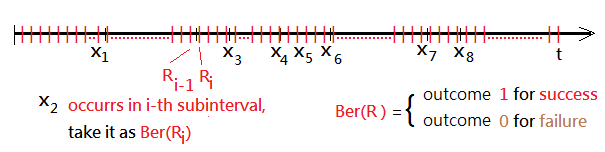 The Bernoulli random variable would have its outcome as $1$ for success and $0$ for failure in its distribution. So the expected value of the $i$-th arrival is:
The Bernoulli random variable would have its outcome as $1$ for success and $0$ for failure in its distribution. So the expected value of the $i$-th arrival is:
$E\lbrack R_{i}\rbrack$=$1\cdot P_{i}$+$0\cdot F_{i}$, where $F_{i}$=$1$-$P_{i}$ for each $i$, and $P_{i}$=$\frac {\lambda\cdot t}{n}$.
➃we then accumulate all outcomes of all $R_{i}$, trivially, the total number of event occurrences remains the same.
$N_{t}$=$R_{1}$+$R_{2}$+…+$R_{i}$+…+$R_{n}$, the point is that each $R_{i}$ is independent random variable, now the original random process behaves in the Binomial distribution as a whole, therefor $N_{t}$ has Binomial distribution of Bin($n$,$p$), where $p$=$\frac {\lambda\cdot t}{n}$.
➄$C_{k}^{n}(\frac {\lambda\cdot t}{n})^{k}\cdot(1-\frac {\lambda\cdot t}{n})^{n-k}$ is the probability we have $k$ arrivals in the Binomial distribution, and the value of $n$ really matters. To get rid of this concern, we treat $n$ as infinity.
$\lim_{n\rightarrow\infty}C_{k}^{n}(\frac {\lambda\cdot t}{n})^{k}\cdot(1-\frac {\lambda\cdot t}{n})^{n-k}$
=$\lim_{n\rightarrow\infty}C_{k}^{n}(\frac {1}{n})^{k}\cdot(\lambda\cdot t)^{k}\cdot(1-\frac {\lambda\cdot t}{n})^{n-k}$
➅$\lim_{n\rightarrow\infty}C_{k}^{n}(\frac {1}{n})^{k}$
=$\lim_{n\rightarrow\infty}\frac {n}{n}\cdot\frac {n-1}{n}\cdot\frac {n-2}{n}\cdot\cdot\cdot\frac {n-k+1}{n}\cdot\frac {1}{k!}$
=$\frac {1}{k!}$…by using some algebra
➆$\lim_{n\rightarrow\infty}(1-\frac {\lambda\cdot t}{n})^{n-k}$
=$\lim_{n\rightarrow\infty}(1-\frac {\lambda\cdot t}{n})^{n}\cdot(1-\frac {\lambda\cdot t}{n})^{k}$
=$e^{-\lambda\cdot t}$
where by calculus, $\lim_{n\rightarrow\infty}(1-\frac {\lambda\cdot t}{n})^{n}$=$e^{-\lambda\cdot t}$,
and $\lim_{n\rightarrow\infty}(1-\frac {\lambda\cdot t}{n})^{k}$=$1$.
➇thus the probability we have $k$ random arrivals is deduced out below:
$P(N_{t}=k)$
=$\lim_{n\rightarrow\infty}C_{k}^{n}(\frac {\lambda\cdot t}{n})^{k}\cdot(1-\frac {\lambda\cdot t}{n})^{n-k}$
=$\lim_{n\rightarrow\infty}C_{k}^{n}(\frac {1}{n})^{k}\cdot(\lambda\cdot t)^{k}\cdot(1-\frac {\lambda\cdot t}{n})^{n-k}$
=$\frac {(\lambda\cdot t)^{k}}{k!}\cdot e^{-\lambda\cdot t}$
The Poisson Distribution Definition
By the illustration step ➇, we have $\frac {(\lambda\cdot t)^{k}}{k!}\cdot e^{-\lambda\cdot t}$ as the probability of $k$ random arrivals, we have below formal claim the definition of the Poisson distribution, as a result of the fact that $e^{-\lambda\cdot t}\cdot\sum_{k=0}^{\infty}\frac {(\lambda\cdot t)^{k}}{k!}$=$1$.
[Definition]
For any discrete random variable X with parameter $\mu$, it is said to have a Poisson distribution if its probability mass function is given by
$P(X=k)$=$\frac {(\mu)^{k}}{k!}\cdot e^{-\mu}$, for $k$=$0$,$1$,$2$,…, denote it as $Pois(\mu)$, where
➀$\mu$=$\lambda\cdot t$, and $\lambda$ is a constant event occurrence rate in the format of (event counts)/(time unit).
➁$t$ is the period of time in the unit with respect to the time unit of the rate by $\lambda$.
Please recall that we use the term probability mass function, since this random process is deducing from a rather discrete distributed case.
Expect Value And Variance Of The Poisson Distribution
Succeeding to above paragraphs, we know that probability for each distinct $R_{j}$ to have event occurrence is $\frac {\lambda\cdot t}{n}$, which is a great add-in and a short-cut to the expect value and variance.
[1]expect value
$E\lbrack N_{t}\rbrack$
=$E\lbrack\sum_{i=1}^{n}R_{i}\rbrack$
=$\sum_{i=1}^{n}E\lbrack R_{i}\rbrack$
=$n\cdot\frac {\lambda\cdot t}{n}$
=$\lambda\cdot t$…hold for $n\rightarrow\infty$
[2]variance::mjtsai
➀begin from the Binomial variance.
$Var\lbrack N_{t}\rbrack$
=$Var\lbrack\sum_{i=1}^{n}R_{i}\rbrack$
=$Var\lbrack R_{1}+R_{2}+…+R_{n}\rbrack$
=$Var\lbrack R_{1}\rbrack$+$Var\lbrack R_{2}\rbrack$+…+$Var\lbrack R_{n}\rbrack$
➁for each $i$,
$Var\lbrack R_{i}\rbrack$
=$E\lbrack R_{i}^{2}\rbrack$-$E^{2}\lbrack R_{i}\rbrack$
=$1^{2}\cdot p+0^{2}\cdot(1-p)$-$p^{2}$
=$p$-$p^{2}$, where $p$ is the success probability
=$p\cdot(1-p)$, take $p$=$\frac {\lambda\cdot t}{n}$
➂go to the Poisson case $n\rightarrow\infty$:
$\lim_{n\rightarrow\infty}Var\lbrack N_{t}\rbrack$
=$\lim_{n\rightarrow\infty}n\cdot p\cdot(1-p)$
=$\lim_{n\rightarrow\infty}n\cdot \frac {\lambda\cdot t}{n}\cdot(1-\frac {\lambda\cdot t}{n})$
=$\lambda\cdot t$, where $\lim_{n\rightarrow\infty}(1-\frac {\lambda\cdot t}{n})$=$1$
You can also see Poisson variance proof on WiKi. We found that the Poisson distribution has the same expect value and variance.
Example: Simple Poisson Probability Illustration
Given that $\lambda$ is the constant rate for the event occurrence over time, then the probability of one arrival within $[0,2s]$ would just be $P(N_{2s}=1)$=$\frac {\lambda\cdot 2s}{1!}\cdot e^{-\lambda\cdot 2s}$.
And one arrival within $[0,2s]$ is identical to the case that one arrival within $[0,s]$, zero arrival within $[s,2s]$ or the case that zero arrival within $[0,s]$, one arrival within $[s,2s]$. Therefore,
$P(N_{2s}=1)$
=$P(N_{[0,s]}=1,N_{[s,2s]}=0)$+$P(N_{[0,s]}=0,N_{[s,2s]}=1)$
=$(\frac {\lambda\cdot s}{1!}\cdot e^{-\lambda\cdot s})\cdot(\frac {(\lambda\cdot s)^{0}}{0!}\cdot e^{-\lambda\cdot s})$+$(\frac {(\lambda\cdot s)^{0}}{0!}\cdot e^{-\lambda\cdot s})\cdot(\frac {\lambda\cdot s}{1!}\cdot e^{-\lambda\cdot s})$
=$\frac {\lambda\cdot 2s}{1!}\cdot e^{-\lambda\cdot 2s}$
Addendum
➀A Modern Introduction to Probability and Statistics, published by Springer.
08 Mar 2018
Prologue To The Hoeffding Bounds
The Hoeffding lemma and Hoeffding inequality are pervasively found in tremendous papers
and lectures in machine learning, statistics, probability theory, such inequality relates the random variables
belonging to the same distribution, to facilitate stepping toward the minimum bias with the suggested sampling size.
The Mjtsai1974 Light Weight Upper Bound
Before stepping into the major topic, make ourself a tiny break in a corner with a rather simple inequality, constrain still the same random variable as Hoeffding lemma. It’s just the trivial finding during my proof in these Hoeffding bounds. I nicknamed it the Mjtsai1974 Light Weight Upper Bound.
Given $X\in\lbrack a,b\rbrack$, it’s a random variable with $E\lbrack x\rbrack$=$0$, then for any $s>0$, we have $E\lbrack e^{s\cdot X}\rbrack\le e^{s\cdot(a-b)}$
proof::mjtsai1974
➀by given $X\in\lbrack a,b\rbrack$, take $\lambda$=$\frac {x-a}{b-a}$,
we just have $x$=$(1-\lambda)\cdot a$+$\lambda\cdot b$.
➁since $g(E\lbrack s\cdot X\rbrack)\le E\lbrack g(s\cdot X)\rbrack$ by Jensen's inequality for any convex function $g(X)$=$e^{X}$, then
$e^{(1-\lambda)\cdot s\cdot a+\lambda\cdot s\cdot b}\le (1-\lambda)\cdot e^{s\cdot a}+\lambda\cdot e^{s\cdot b}$
$\Rightarrow E\lbrack e^{(1-\lambda)\cdot s\cdot a+\lambda\cdot s\cdot b}\rbrack\le E\lbrack (1-\lambda)\cdot e^{s\cdot a}+\lambda\cdot e^{s\cdot b}\rbrack$
➂that is to say, for any $x\in X$, we have
$E\lbrack e^{s\cdot x}\rbrack$
$\le E\lbrack (1-\lambda)\cdot e^{s\cdot a}+\lambda\cdot e^{s\cdot b}\rbrack$
=$E\lbrack (\lambda+(1-\lambda)\cdot e^{s\cdot a-s\cdot b})\cdot e^{s\cdot b}\rbrack$
=$E\lbrack (\frac {x-a}{b-a}+(\frac {b-x}{b-a})\cdot e^{s\cdot a-s\cdot b})\cdot e^{s\cdot b}\rbrack$
=$(\frac {-a}{b-a}+(\frac {b}{b-a})\cdot e^{s\cdot (a-b)})\cdot e^{s\cdot b}$…$E\lbrack x\rbrack$=$0$
, which is equivalent to ask for its approximation.
➃take $p$=$\frac {-a}{b-a}$, then $1-p$=$\frac {b}{b-a}$. From the two equalities, we can deduce out two expressions for $b$:
$b$=$\frac {a\cdot (p-1)}{p}$ and $b$=$(1-p)\cdot (b-a)$
Choose $b$=$(1-p)\cdot (b-a)$ to express $b$, then above inequality becomes
$E\lbrack e^{s\cdot x}\rbrack$
$\le (\frac {-a}{b-a}+(\frac {b}{b-a})\cdot e^{s\cdot (a-b)})\cdot e^{s\cdot b}$
=$((1-p)\cdot e^{s\cdot (a-b)}+p)\cdot e^{s\cdot (1-p)\cdot (b-a)}$
=$((1-p)\cdot e^{s\cdot (a-b)}+p)\cdot e^{s\cdot (p-1)\cdot (a-b)}$
The reason we choose such $b$ expression is to simplify the inequality.
➄take $u$=$a-b$,$\theta(u)$=$((1-p)\cdot e^{s\cdot u}+p)\cdot e^{s\cdot (p-1)\cdot u}$, then
$ln\theta(u)$
=$ln((1-p)\cdot e^{s\cdot u}+p)$+$s\cdot (p-1)\cdot u$
$\le ln((1-p)\cdot e^{s\cdot u}+p)$…since $p-1\le 0$
$\le ln((1-p)\cdot e^{s\cdot u})$…since $p\le 1$
$\le ln(e^{s\cdot u})$
=$s\cdot u$
, then $\theta(u)\le e^{s\cdot u}$
Therefore, $E\lbrack e^{s\cdot X}\rbrack\le e^{s\cdot(a-b)}$ is thus proved, this is a simple, light weight inequality, I denote it Mjtsai1974 Light Weight Upper Bound.
The Hoeffding Lemma
Given $X\in\lbrack a,b\rbrack$, it’s a random variable with $E\lbrack x\rbrack$=$0$, then for any $s>0$, we have $E\lbrack e^{s\cdot X}\rbrack\le e^{\frac {s^2\cdot(b-a)^2}{8}}$
proof::mjtsai1974
We would inherit from ➄ in the proof of Mjtsai1974 Light Weight Upper Bound, begin from $ln\theta(u)$=$ln((1-p)\cdot e^{s\cdot u}+p)$+$s\cdot (p-1)\cdot u$, where $u$=$a-b$,$\theta(u)$=$((1-p)\cdot e^{s\cdot u}+p)\cdot e^{s\cdot (p-1)\cdot u}$.
➀take $M(u)$=$ln\theta(u)$, by Taylor theorem, for $w\in\lbrack u,0\rbrack$, where in this case $u\le 0$, we have
$\lim_{w\rightarrow u}M(w)$
$\approx ln\theta(u)$+$\frac {ln^{′}\theta(u)}{1!}\cdot (w-u)$+$\frac {ln^{″}\theta(u)}{2!}\cdot (w-u)^2$+$\frac {ln^{′″}\theta(u)}{3!}\cdot (w-u)^3$+…
$\le ln\theta(0)$+$\frac {ln^{′}\theta(0)}{1!}\cdot (0-u)$+$\frac {ln^{″}\theta(0)}{2!}\cdot (0-u)^2$+$\frac {ln^{′″}\theta(0)}{3!}\cdot (0-u)^3$+…
➁from above, we must make first, second derivatives, they are
$ln^{′}\theta(u)$=$(p+(1-p)\cdot e^{s\cdot u})^{-1}\cdot ((1-p)\cdot s\cdot e^{s\cdot u})$+$s\cdot(p-1)$
$ln^{″}\theta(u)$=$-1\cdot (p+(1-p)\cdot e^{s\cdot u})^{-2}\cdot ((1-p)\cdot s\cdot e^{s\cdot u})^{2}$
$\;\;\;\;\;\;\;\;+(p+(1-p)\cdot e^{s\cdot u})^{-1}\cdot ((1-p)\cdot s^2\cdot e^{s\cdot u})$
And, $ln\theta(0)$=$0$, $ln^{′}\theta(0)$=$0$,
$ln^{″}\theta(0)$=$-1\cdot((1-p)\cdot s)^2$+$(1-p)\cdot s^2$=$p\cdot (1-p)\cdot s^2$
➂therefore, we’d like to maximum the term $ln^{″}\theta(u)$,
take $z$=$e^{s\cdot u}$, $s$=$\frac {ln(z)}{u}$, then
$ln^{″}\theta(u)$…further regularized
=$\frac {p\cdot (1-p)\cdot s^2\cdot e^{s\cdot u}}{(p+(1-p)\cdot e^{s\cdot u})^{2}}$
=$\frac {p\cdot (1-p)\cdot (\frac {ln(z)}{u})^2\cdot z}{(p+(1-p)\cdot z)^{2}}$
$\le \frac {p\cdot (1-p)\cdot z}{(p+(1-p)\cdot z)^{2}}$…$(\frac {ln(z)}{u})^2\le 1$
➃take $N(z)$=$\frac {p\cdot (1-p)\cdot z}{(p+(1-p)\cdot z)^{2}}$, and $ln^{″}\theta(u)$=$s^2\cdot N(z)$, this is equivalent to ask for the maximum of $N(z)$, the formal procedure would be to take its first derivative and set it to $0$, next to get the possible $z$ expressed in terms of $p$, in this case, $z$ is the input parameter in $N(z)$.
$N′(z)$=$\frac {p^{2}\cdot (1-p)-p\cdot (1-p)^{2}\cdot z}{(p+(1-p)\cdot z)^{3}}$=$0$
After we solve it, we get $z$=$\frac {p}{1-p}$ is the critical point.
➄take $z$=$\frac {p}{1-p}$ in $N(z)$
$N(z)$=$\frac {p\cdot (1-p)\cdot\frac {p}{1-p}}{(p+(1-p)\cdot\frac {p}{1-p})^{2}}$=$\frac {p^{2}}{4\cdot p^{2}}$=$\frac {1}{4}$
Be recalled that $ln^{″}\theta(u)$=$s^2\cdot N(z)$, back to the Taylor expansion in ➁, we have
$ln\theta(u)$
=$M(u)$
$\le \frac {ln^{″}\theta(0)}{2!}\cdot(u)^{2}$
=$\frac {s^{2}\cdot N(z)}{2!}\cdot (u)^2$
$\le \frac {1}{2!}\cdot s^{2}\cdot\frac {1}{4}\cdot u^{2}$
=$\frac {1}{8}\cdot s^{2}\cdot u^{2}$
Therefore, $\theta(u)\le e^{\frac {1}{8}\cdot s^{2}\cdot u^{2}}$
➅finally, we just proved that
$E\lbrack e^{s\cdot X}\rbrack\le \theta(u)\le e^{\frac {1}{8}\cdot s^{2}\cdot u^{2}}$=$e^{\frac {s^{2}\cdot (a-b)^{2}}{8}}$=$e^{\frac {s^{2}\cdot (b-a)^{2}}{8}}$
The Hoeffding Inequality
Given that $X_1$,$X_2$,,,$X_n$ are independent random variables with $a_i\le X_i\le b_i$, then
$\;\;\;\;P(\frac {1}{n}\cdot\sum_{1}^{n}(X_i-E\lbrack X_i\rbrack)\ge\varepsilon)\le exp(\frac {-2\cdot n^2\cdot\varepsilon^2}{\sum_{1}^{n}(b_i-a_i)^2})$
Proof:
We’d like to prove it by Hoeffding lemma.
➀take $Z_i$=$X_i-E\lbrack X_i\rbrack$, for all $i$, then $Z_i\in\lbrack a_i,b_i\rbrack$ and $E\lbrack Z_i\rbrack$=$0$ just holds.
$P(\frac {1}{n}\cdot\sum_{i=1}^{n}(X_i-E\lbrack X_i\rbrack))$=$P(\frac {1}{n}\cdot\sum_{i=1}^{n}(Z_i))$, then
$P(\frac {1}{n}\cdot\sum_{i=1}^{n}(X_i-E\lbrack X_i\rbrack)\ge\varepsilon)$=$P(\frac {1}{n}\cdot\sum_{i=1}^{n}(Z_i)\ge\varepsilon)$
$\Rightarrow P(\sum_{i=1}^{n}(X_i-E\lbrack X_i\rbrack)\ge n\cdot\varepsilon)$=$P(\sum_{i=1}^{n}(Z_i)\ge n\cdot\varepsilon)$
➁take $t$=$n\cdot\varepsilon$, then we have
$P(\sum_{i=1}^{n}(Z_i)\ge n\cdot\varepsilon)$
=$P(\sum_{i=1}^{n}(Z_i)\ge t)$
=$P(exp(\sum_{i=1}^{n}(s\cdot Z_i))\ge exp(s\cdot t))$
$\le E\lbrack (\prod_{i=1}^{n}exp(s\cdot Z_i))\rbrack\cdot exp(-s\cdot t)$
=$\prod_{i=1}^{n} E\lbrack exp(s\cdot Z_i)\rbrack\cdot exp(-s\cdot t)$
$\le exp(-s\cdot t)\cdot\prod_{i=1}^{n} exp(\frac {s^2\cdot (b_i-a_i)^2}{8})$
=$exp(\sum_{i=1}^{n}\frac {s^2\cdot (b_i-a_i)^2}{8}-s\cdot t)$
➂it’s equivalent to find the minimum of the term, the formal procedure would be to take the first derivative with respect to $s$, set it to $0$, solve $s$ in terms of $t$, since $s$ is a further expanded term in the proof process, we should eliminate $s$.
After that we find $s$=$\frac {4\cdot t}{\sum_{i=1}^{n}(b_i-a_i)^2}$ is the critical point.
Therefore,$P(\sum_{i=1}^{n}(Z_i)\ge t)\le exp(\frac {-2\cdot t^2}{\sum_{i=1}^{n}(b_i-a_i)^2})$
Finally, replace $t$ with $n\cdot\varepsilon$, we have it proved that
$P(\sum_{i=1}^{n}(Z_i)\ge n\cdot\varepsilon)\le exp(\frac {-2\cdot n^2\cdot\varepsilon^2}{\sum_{i=1}^{n}(b_i-a_i)^2})$
If we are given all $Z_i\in\lbrack a,b\rbrack$, then the inequality would become
$P(\sum_{i=1}^{n}(Z_i)\ge n\cdot\varepsilon)\le exp(\frac {-2\cdot n\cdot\varepsilon^2}{(b-a)^2})$
By symmetry, we have it that
$P(\vert\sum_{i=1}^{n}(Z_i)\vert\ge n\cdot\varepsilon)\le$ 2$\cdot exp(\frac {-2\cdot n\cdot\varepsilon^2}{(b-a)^2})$
$\Rightarrow P(\vert\sum_{i=1}^{n}(X_i-E\lbrack X_i\rbrack)\vert\ge n\cdot\varepsilon)\le$ 2$\cdot exp(\frac {-2\cdot n\cdot\varepsilon^2}{(b-a)^2})$
05 Mar 2018
Prologue To The Symmetrization
In machine learning, statistics, probability theory, the symmetrization is commonly used to relate the random variables belonging to the same distribution.
The Symmetrization
Given a bounded random variable $Z\in\lbrack a,b\rbrack$, we perform multiple tests of it with instances of $Z$ duplicated, choose one of the clones to be $Z’$, so that $Z’\in\lbrack a,b\rbrack$ and $E\lbrack Z\rbrack$=$E\lbrack Z’\rbrack$.
There exists some properties:
[1]$E_Z\lbrack e^{Z-E\lbrack Z\rbrack}\rbrack\le E_Z\lbrack E_{Z’}\lbrack e^{Z-Z’}\rbrack\rbrack$
[2]$P(\left|Z-E\lbrack Z\rbrack\right|\ge t)$=$P(\left|Z-E\lbrack Z’\rbrack\right|\ge t)$
$\le E\lbrack e^{\lambda\cdot E\lbrack\left|Z-Z’\right|\rbrack}\rbrack\cdot e^{-\lambda\cdot t}$
[3]$E_Z\lbrack E_{Z’}\lbrack e^{\lambda\cdot (Z-Z’)}\rbrack\rbrack\le e^{\frac {(\lambda\cdot (b-a))^{2}}{2}}$
proof::mjtsai1974
➀by given, $E\lbrack Z\rbrack$=$E\lbrack Z’\rbrack$, then,
$E_Z\lbrack Z-E\lbrack Z\rbrack\rbrack$=$E_Z\lbrack Z-E\lbrack Z’\rbrack\rbrack$
And according to the Jensen's inequality, we have it that
$E_Z\lbrack e^{Z-E\lbrack Z\rbrack}\rbrack$
=$E_Z\lbrack e^{Z-E\lbrack Z’\rbrack}\rbrack$
$\le E_Z\lbrack E_{Z’}\lbrack e^{Z-Z’}\rbrack\rbrack$
➁by the Chernoff bounds, we can have
$P(\left|Z-E\lbrack Z\rbrack\right|\ge t)$
=$P(\left|Z-E\lbrack Z’\rbrack\right|\ge t)$
=$P(e^{\lambda\cdot\left|Z-E\lbrack Z’\rbrack\right|}\ge e^{\lambda\cdot t})$
$\le E\lbrack e^{\lambda\cdot\left|Z-E\lbrack Z’\rbrack\right|}\rbrack\cdot e^{-\lambda\cdot t}$
$\le E\lbrack e^{\lambda\cdot E\lbrack\left|Z-Z’\right|\rbrack}\rbrack\cdot e^{-\lambda\cdot t}$
➂given that $S\in\{+1,-1\}$, a Rademacher random variable, and $S\cdot (Z-Z')$ and $Z-Z'$ have the same distribution, it implies that
$E_Z\lbrack E_{Z’}\lbrack e^{Z-Z’}\rbrack\rbrack$
=$E_Z\lbrack E_{Z’}\lbrack e^{S\cdot (Z-Z’)}\rbrack\rbrack$
=$E_{Z,Z’}\lbrack E_{S}\lbrack e^{S\cdot (Z-Z’)}\rbrack\rbrack$
Then, below holds,
$E_Z\lbrack E_{Z’}\lbrack e^{\lambda\cdot (Z-Z’)}\rbrack\rbrack$
=$E_Z\lbrack E_{Z’}\lbrack e^{S\cdot\lambda\cdot (Z-Z’)}\rbrack\rbrack$
=$E_{Z,Z’}\lbrack E_{S}\lbrack e^{S\cdot\lambda\cdot (Z-Z’)}\rbrack\rbrack$
➃by MGF, we have below holds
$E_{S}\lbrack e^{S\cdot\lambda\cdot (Z-Z’)}\rbrack\le e^{\frac {(\lambda\cdot (Z-Z’))^{2}}{2}}$
Because $\left|Z-Z'\right|\le (b-a)$ guarantees $(Z-Z')^{2}\le (b-a)^{2}$ , then
$E_{S}\lbrack e^{S\cdot\lambda\cdot (Z-Z’)}\rbrack\le e^{\frac {(\lambda\cdot (b-a))^{2}}{2}}$
Therefore, $E_Z\lbrack E_{Z’}\lbrack e^{\lambda\cdot (Z-Z’)}\rbrack\rbrack\le e^{\frac {(\lambda\cdot (b-a))^{2}}{2}}$
➁by above table, we just need to accumulate the probability of the case (1) and (2), which is equivalent to substract the probability of two event occurrences in $(s,t]$ from the probability that two event arrivals in $[0,t]$.
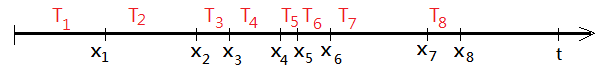
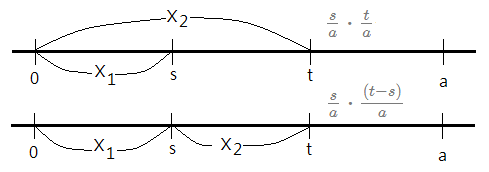
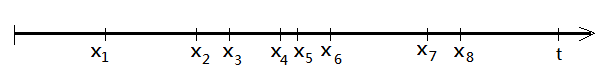 This article denotes the total number of occurrences within $[0,t]$ as $N([0,t])$, or just abbreviating $N_{t}$ for over time length $t$. The homogeneity implies that $E\lbrack N_{t}\rbrack$=$\lambda\cdot t$.
This article denotes the total number of occurrences within $[0,t]$ as $N([0,t])$, or just abbreviating $N_{t}$ for over time length $t$. The homogeneity implies that $E\lbrack N_{t}\rbrack$=$\lambda\cdot t$.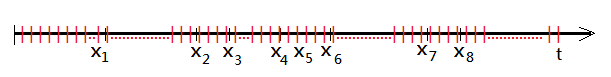 Then we have each distinct subinterval of time length $\frac {1}{n}$, and each subinterval would just have success of $1$ arrival, or failure of $0$ arrival, which itself is a Bernoulli distribution.
Then we have each distinct subinterval of time length $\frac {1}{n}$, and each subinterval would just have success of $1$ arrival, or failure of $0$ arrival, which itself is a Bernoulli distribution. The Bernoulli random variable would have its outcome as $1$ for success and $0$ for failure in its distribution. So the expected value of the $i$-th arrival is:
The Bernoulli random variable would have its outcome as $1$ for success and $0$ for failure in its distribution. So the expected value of the $i$-th arrival is: