14 May 2018
Prologue To Unbiased Estimator And Random Sample
Unbiased estimator is a device or method to estimate the quantity of interesting features in a model distribution. Such estimation is made on the dataset from random samples.
Random Sample And Sample Statistic
➀a random sample is a collection of random variables, say $X_1$,$X_2$,…,$X_n$, they have the same probability distribution and are assumed to be mutually independent. Those random variables thus constitute a random sample of population.
➁sampling is the behavior of taking samples from a population, it must be representative to the population from which it is obtained.
➂whereas, datasets are usually modelled as the realization of random samples, $X_1$,…,$X_n$.
➃sample statistic is an object, which depends on the random samples, $X_1$,…,$X_n$. To be more formally, the sample average $\overline {X_n}$ is just one of the commonly referenced sample statistic.
You can also take one distinct random random variable $X$ as a random sample; although we often expect multiple random variables in a set of random sample.
Estimate versus Estimator
➀the estimate is the pure quantity obtained by means of the estimator.
➀the estimator is an artificial designed random variable by taking parameters constituting to a model distribution.
The value of $\overline {X_n}$ is the estimate, $\frac {X_1+X_2+...+X_n}{n}$ is just the estimator.
Unbiased Estimator And Sampling Distribution
➀assume the random variable $T$ is an estimator based on random sample consisting of $X_1$,$X_2$,…,$X_n$ for the quantity of features of interest, the distribution of the estimator $T$ is the sampling distribution of $t$.
➁the random variable $T$ is an unbiased estimator of the feature, denoted it as $\theta$, if and only if $E\lbrack T\rbrack$=$\theta$, for any value of $\theta$.
Unbiased Estimator For Sample Expectation
This section focus on the quantity of interest, the expect value of random sample.
Irrelevant of the original probabilistic distribution
of the random sample, $\overline {X_n}$=$\frac {X_1+X_2+...+X_n}{n}$ is an unbiased estimator for the sample expectation, given that the sample is consisting of $X_1$,…,$X_n$, with $\mu$ and $\sigma^2$ as its finite expectation and variance.
proof:
$E\lbrack \overline {X_n}\rbrack$
=$E\lbrack \frac {X_1+X_2+…+X_n}{n}\rbrack$
=$\sum_{i=1}^{n}\frac {E\lbrack X_i\rbrack}{n}$
=$\sum_{i=1}^{n}\frac {\mu}{n}$
=$\mu$
This proof is rather trivial.
Unbiased Estimator For Sample Variance
This section focus on the quantity of interest, the variance of random sample.
Irrelevant of the original probabilistic distribution
of the random sample, $S_n^{2}$=$\sum_{i=1}^{n}\frac {(X_i-\overline {X_n})^{2}}{n-1}$ is an unbiased estimator for the sample variance, given that the sample is consisting of $X_1$,…,$X_n$, with $\mu$ and $\sigma^2$ as its finite expectation and variance.
proof:
➀we begin by the most basic definition of variance.
$E\lbrack \sum_{i=1}^{n}(X_i-\overline {X_n})^{2}\rbrack$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu+\mu-\overline {X_n})^{2}\rbrack$
=$E\lbrack \sum_{i=1}^{n}((X_i-\mu)-(\overline {X_n}-\mu))^{2}\rbrack$
➁expand the summation term.
$\sum_{i=1}^{n}((X_i-\mu)-(\overline {X_n}-\mu))^{2}$
=$\sum_{i=1}^{n}(X_i-\mu)^{2}$-$2\cdot\sum_{i=1}^{n}(X_i-\mu)\cdot(\overline {X_n}-\mu)$+$\sum_{i=1}^{n}(\overline {X_n}-\mu)^{2}$
; where $\sum_{i=1}^{n}(\overline {X_n}-\mu)^{2}$=$n\cdot(\overline {X_n}-\mu)^{2}$, and
$\sum_{i=1}^{n}(X_i-\mu)\cdot(\overline {X_n}-\mu)$
=$(\overline {X_n}-\mu)\cdot\sum_{i=1}^{n}(X_i-\mu)$
=$(\overline {X_n}-\mu)\cdot(\sum_{i=1}^{n}X_i-n\cdot\mu)$
=$(\overline {X_n}-\mu)\cdot(n\cdot\overline {X_n}-n\cdot\mu)$
=$n\cdot (\overline {X_n}-\mu)^{2}$
➂therefore, original expression becomes:
$E\lbrack \sum_{i=1}^{n}(X_i-\overline {X_n})^{2}\rbrack$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu)^{2}$-$2\cdot\sum_{i=1}^{n}(X_i-\mu)\cdot(\overline {X_n}-\mu)$+$\sum_{i=1}^{n}(\overline {X_n}-\mu)^{2}\rbrack$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu)^{2}$-$2\cdot n\cdot (\overline {X_n}-\mu)^{2}$+$n\cdot(\overline {X_n}-\mu)^{2}\rbrack$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu)^{2}$-$n\cdot (\overline {X_n}-\mu)^{2}\rbrack$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu)^{2}\rbrack$-$n\cdot E\lbrack (\overline {X_n}-\mu)^{2}\rbrack$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu)^{2}\rbrack$-$n\cdot E\lbrack (\overline {X_n}-E\lbrack \overline {X_n}\rbrack)^{2}\rbrack$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu)^{2}\rbrack$-$n\cdot Var\lbrack \overline {X_n}\rbrack$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu)^{2}\rbrack$-$n\cdot \frac {\sigma^{2}}{n}$
=$E\lbrack \sum_{i=1}^{n}(X_i-\mu)^{2}\rbrack$-$\sigma^{2}$
=$\sum_{i=1}^{n}E\lbrack (X_i-\mu)^{2}\rbrack$-$\sigma^{2}$
=$\sum_{i=1}^{n}E\lbrack (X_i-E\lbrack X_i\rbrack)^{2}\rbrack$-$\sigma^{2}$
; where $E\lbrack X_i\rbrack$=$\mu$,$E\lbrack (X_i-E\lbrack X_i\rbrack)^{2}$=$\sigma^2$
=$\sum_{i=1}^{n}\sigma^{2}$-$\sigma^{2}$
=$(n-1)\cdot\sigma^{2}$
➃from $E\lbrack \sum_{i=1}^{n}(X_i-\overline {X_n})^{2}\rbrack$=$(n-1)\cdot\sigma^{2}$,
we can have $E\lbrack \sum_{i=1}^{n}\frac {(X_i-\overline {X_n})^{2}}{n-1}\rbrack$=$\sigma^{2}$
Example: Unbiased Estimator Doesn't Always Hold
This article has shown the unbiased estimator of sample expectation and variance. Cautions must be made that the unbiased estimator doesn't always hold.
The mathematics thing can reveal it explicitly by means of the Jensen’s inequality, which claims that $g(E\lbrack X\rbrack)$<$E\lbrack g(X)\rbrack$, where $g(X)$ is a convex function.
[1]
Suppose that we have $g(X)$=$X^{2}$, which is strictly a convex function.
➀ take $X$=$S_n$, then
$g(E\lbrack X\rbrack)$=$g(E\lbrack S_n\rbrack)$=$E^{2}\lbrack S_n\rbrack$<$E\lbrack g(S_n)\rbrack$=$E\lbrack S_n^{2}\rbrack$=$\sigma^{2}$
➁ it implies that $E\lbrack S_n\rbrack$<$\sigma$, the unbiased estimator doesn't always hold, even if we are given that $S_n^2$ is an unbiased estimator of $\sigma^{2}$. In this case, $E\lbrack S_n\rbrack$ is not an unbiased estimator for $\sigma$.
[2]
Suppose that we have $g(X)$=$e^{-X}$ for the zero arrival probability, $p_0$=$e^{-\mu}$, in Pois($\mu$) distribution, say $\mu$=$E\lbrack\overline {X_n}\rbrack$, can we take $e^{-\overline {X_n}}$ for the unbiased estimator of zero arrival probability?
➀begin from Jensen’s inequality,
$E\lbrack e^{-\overline {X_n}}\rbrack$=$E\lbrack g(\overline {X_n})\rbrack$>$g(E\lbrack \overline {X_n}\rbrack)$=$e^{-E\lbrack\overline {X_n}\rbrack}$=$e^{\mu}$
➁hence, $e^{-\overline {X_n}}$ is not an unbiased estimator for the zero arrival probability.
Suggestion is to be made to use $\overline {X_n}$ to be the unbiased estimator of $\mu$, as $n\rightarrow\infty$, the law of large numbers would guarantee $E\lbrack\overline {X_n}\rbrack$=$\mu$, finally, by using $e^{E\lbrack\overline {X_n}\rbrack}$ to approximate the zero arrival probability.
12 May 2018
Prologue To The Central Limit Theorem
The central limit theorem is a refinement of the law of large number. For a large number of random variables $X_1$,$X_2$,...,$X_n$, with converged expect value and finite variance, the standardization process would settle down $\overline {X_n}$ in a normal distribution, irrelevant to the original distribution these $X_i$ is belonging to.
Standardizing The Average
Given a large number of random variables $X_i$ belonging to the same sample, with the same expect value $\mu$ and variance $\sigma^{2}$, the law of large number guarantees the average would approximate to $\mu$.
Here comes the question as what is the distribution of $\overline {X_n}$? Since each random variables $X_i$ has the same $\mu$ and $\sigma^{2}$, it would be a good idea to stablize the expect value and variance of $\overline {X_n}$.
We already know $E\lbrack \overline{X_n}\rbrack$=$\mu$ and $Var\lbrack \overline{X_n}\rbrack$=$\frac {\sigma^{2}}{n}$. What would be the acceptable expect value with regards to the stablized variance?
➀by $E\lbrack \overline{X_n}-\mu\rbrack$=$0$, we can zerolize the expect value, to be believed the smallest value.
➁next to make the variance stable, suppose there exists any $c>0$ such that $Var\lbrack c\cdot\overline{X_n}\rbrack$ could be well stablized. If we can factor out whatever the variance residing in the distribution of $\overline {X_n}$ itself, then there will be a hope. For unknown distribution, this is quiet difficult.
➂but, we would make it easy by taking $c=\frac {\sqrt n}{\sigma}$, the mathematic thing guarantees the purity and balance of the variance, since $Var\lbrack \frac {\sqrt n}{\sigma}\cdot\overline{X_n}\rbrack$=$\frac {n}{\sigma^{2}}\cdot Var\lbrack \overline{X_n}\rbrack$=$1$
➃$Var\lbrack \frac {\sqrt n}{\sigma}\cdot(\overline{X_n}-\mu)\rbrack$
=$Var\lbrack \frac {\sqrt n}{\sigma}\cdot\overline{X_n}\rbrack$, we can further stablize the variance in a centered average format.
Above procedure is the standardization or the standardize process.
The Central Limit Theorem
Given $X_1$,$X_2$,…,$X_n$ are identically independent distributed random variables, each has the same expect value $\mu$ and variance $\sigma^{2}$, which are all finite.
For any $n\ge 1$, let $Z_n$ be any random variable, defined by
$\;\;\;\;Z_n$=$\frac {\overline {X_n}-\mu}{\sigma/\sqrt {n}}$;
then, $E\lbrack Z_n\rbrack$=$0$ and $Var\lbrack Z_n\rbrack$=$1$.
$Z_n$ itself is the standard normal distribution, $N(0,1)$
, for any $a$, we have $F_{Z_n}(a)$=$ɸ(a)$.
We treat $Z_n$ as the standardized $\overline {X_n}$.
Example: Illustration Of The Central Limit Theorem
Suppose you are given a random sample of size $500$ containing random variables $X_1$,$X_2$,…,$X_{500}$, all of them coming from the same unknown distribution with each having expect value $2$ and variance also $2$.
After completing all the $500$ runs of test, we get the experiement average of $\overline {X_n}$=$2.06$, do you think it a plausible result?
To answer this question, we have to compute the probability of the case that $\overline {X_n}$ is greater than or equal to $2.06$.
$P(\overline {X_n}\ge 2.06)$
=$P(\overline {X_n}-\mu\ge 2.06-\mu)$
=$P(\frac {\overline {X_n}-\mu}{\sigma/\sqrt {n}}\ge \frac {2.06-\mu}{\sigma/\sqrt {n}})$
=$P(\frac {\overline {X_{500}}-\mu}{\sigma/\sqrt {500}}\ge \frac {2.06-2}{\sqrt {2}/\sqrt {500}})$…$\mu$=$2$,$\sigma$=$\sqrt {2}$
=$P(Z_{500}\ge 0.95)$
=1-$P(Z_{500}<0.95)$
=1-$ɸ(0.95)$
$\approx 0.1711$, it indicates that there exists probability of $0.1711$ that the average is $0.06$ larger than $2$, the expect value of the real thing.
Since $0.1711$ is quiet a large probability, it is rather weak to say that $2.06$ is an abnormal experimental result of average. $2.06$ would thus be plausible.
11 May 2018
Prologue To The Law Of Large Number
Based on the result of the Chebyshev's inequality, the law of large number guarantees the precision of the averaged term quantity of interest would be well approximated to the mean of the term in the sample data.
The Chebyshev's Inequality
For $X$ to be any arbitrary random variable, and for ang given $a>0$:
$\;\;\;\;P(|X-E\lbrack X\rbrack|\ge a)\le \frac {1}{a^{2}}\cdot Var\lbrack X\rbrack$
proof::➀
Please go to the article Hoeffding Inequality v.s. Chebyshev’s Inequality
proof::➁
Or you can see it in Chebyshev’s Inequality
Theorem: The Law Of Large Number
Given random variables $X_1$,$X_2$,…,$X_n$, each is identically independent distributed with mean $\mu$ and variance $\sigma^{2}$.
$\;\;\;\;\lim_{n\rightarrow\infty}P(|\overline {X_n}-E\lbrack \overline {X_n}\rbrack|\ge \varepsilon)$=$0$
proof:
➀trivially, we know that $E\lbrack \overline {X_n}\rbrack$=$\mu$, $Var\lbrack \overline {X_n}\rbrack$=$\frac {\sigma^{2}}{n}$.
➁by using the Chebyshev's inequality, we have:
$P(|\overline {X_n}-E\lbrack \overline {X_n}\rbrack|\ge \varepsilon)$
=$P(|\overline {X_n}-\mu|\ge \varepsilon)$
$\le \frac {Var\lbrack \overline {X_n}\rbrack}{\varepsilon^{2}\cdot n}$
=$\frac {\sigma^{2}}{\varepsilon^{2}\cdot n}$, for any $\varepsilon>0$
➂$\lim_{n\rightarrow\infty}P(|\overline {X_n}-E\lbrack \overline {X_n}\rbrack|\ge \varepsilon)\le\lim_{n\rightarrow\infty}\frac {\sigma^{2}}{\varepsilon^{2}\cdot n}$, as $n\rightarrow\infty$, it holds that $\lim_{n\rightarrow\infty}P(|\overline {X_n}-E\lbrack \overline {X_n}\rbrack|\ge \varepsilon)$=$0$
Cautions must be made that the law of large number might fail if the expect value is infinite!!!
Example: Illustration Of The Law Of Large Number For Discrete Random Variable
The execution of a random variable would be the event.
In this example, we’d like to know the probability of this event occurrence.
➀if we treat $p$=$P(X\in C)$, where $C=(a,b]$ for $a<b$, we’d like to estimate this probability $p$. The most usual way is by using the relative frequency of $X_i\in C$ among $X_1$,$X_2$,…,$X_n$, that is the number of times $X_i$ hits $C$ divided by $n$.
➁we then define the random variable by
$Y_i$=\(\left\{\begin{array}{l}1, for X_i\in C\\0, for X_i\not\in C\end{array}\right.\)
; where above $X_i$ is just event, $Y_i$ just indicates whether $X_i$ hits $C$ for all $i$. Each execution of $Y_i$ would we obtain the event $X_i$ occurrence probability, and is only determined by $X_i$, therefore, $Y_i$ is identically independent distributed.
➂the expect value and variance of each $Y_i$:
$E\lbrack Y_i\rbrack$=$1\cdot P(X\in C)$+$0\cdot P(X\not\in C)$=$p$
$Var\lbrack Y_i\rbrack$=$E\lbrack (Y_i-E\lbrack Y_i\rbrack)^{2}\rbrack$=$E\lbrack Y_i^{2}\rbrack$-$E^{2}\lbrack Y_i\rbrack$=$p-p^{2}$=$p\cdot(1-p)$
➃the relative frequency is in this expression:
$\overline {Y_n}$=$\frac {Y_1+Y_2+…+Y_n}{n}$, then
$E\lbrack \overline {Y_n}\rbrack$=$\sum_{i=1}^{n}\frac {E\lbrack Y_i\rbrack}{n}$=$p$
$Var\lbrack \overline {Y_n}\rbrack$=$Var\lbrack \sum_{i=1}^{n}\frac {Y_i}{n}\rbrack$=$\frac {p\cdot(1-p)}{n}$
➄then, $\lim_{n\rightarrow\infty}P(|\overline {Y_n}-p|\ge \varepsilon)$=$0$, for any $\varepsilon>0$, since it is upper bounded to $\frac {p\cdot(1-p)}{\varepsilon^{2}\cdot n}$.
Example: Illustration Of The Law Of Large Number For Continuous Random Variable
We next have a look at the continuous case.
➀consider that $f$ is a PDF with respect to $F$, which is a CDF. Choose $C=(a-h,a+h]$, where $h$ is some very small positive value.
➁by above example equation, it holds to have:
$\overline {Y_n}\approx p$
=$P(X\in C)$
=$\int_{a-h}^{a+h}f(x)\operatorname dx$
$\approx 2\cdot h\cdot f(a)$
➂then, $f(a)\approx\frac {\overline {Y_n}}{2\cdot h}$, which is just the number of times $X_i$ hits $C$ for $i<n$, divided by the length of $C$.
03 May 2018
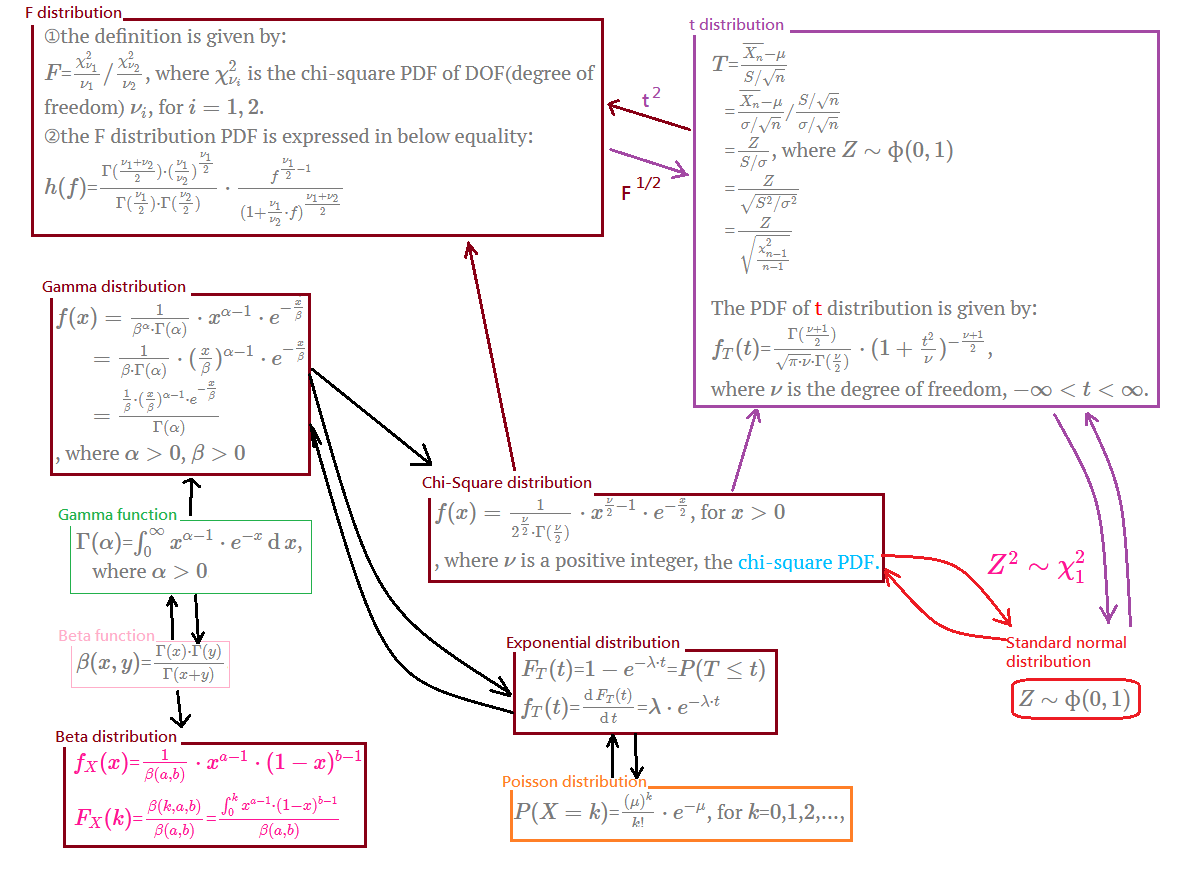
Prologue To The relation in between The Normal, F, Chi-Square, t, Exponential, Poisson Distributions
The normal, F, chi-square, t, exponential, Poisson distributions are all interconnected, even more the random arrival investigation reveals that the exponential, Poisson distributions are the same for the condition that the very first arrival occurrence after the first arrival interval. Most of those distributions are developed based on the gamma function.
Brief Summary
Here, I am just exhibiting the interconnection by graph.
25 Apr 2018
Prologue To Exponential versus Poisson Distribution::mjtsai1974
In the world of stochasticity, pass and failure evaluation often been proceeded under the assumption that the intensity of event occurrence is constant over time, which is debatable.
When we involve the reinforcement learning issues, or the statistics regression topics, although the discrete case is easily constructed and simulated by bootstrapping algorithm in conjunction with the maximum likelihood estimation, the migration to continuous case would be just to split the test horizon into many, many, uncountable subintervals.
Then, that connects the Poisson distribution to the exponential distribution, and the random arrivals probability could be modelled by gamma distribution as a result of the nature of exponential distribution.
Overview The Similarities And Differences
[1]
the Poisson distribution
➀we have an assumption that the intensity of event occurrence over time is invariant for Poisson process.
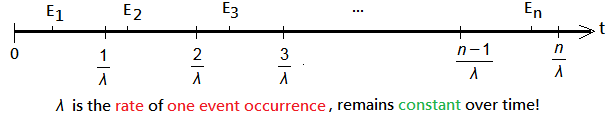
➁suppose it is $\lambda$=$\frac {event\;counts}{time\;length}$
Below exhibits the case where $\lambda$=$\frac {1}{time\;length}$.
 This is the case where $\lambda$=$\frac {k}{time\;length}$.
This is the case where $\lambda$=$\frac {k}{time\;length}$.
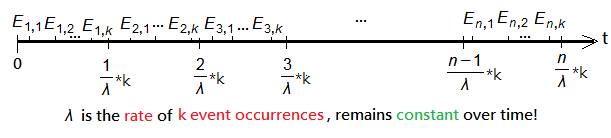 ➂it takes up time length of $\frac {k}{\lambda}$ to have $k$ random arrivals, for $\lambda$=$\frac {k}{time\;length}$. So, it holds to say that the adjacent two events of random arrival would just take time $\frac {1}{\lambda}$, which is the ideal inter-arrival times.
➂it takes up time length of $\frac {k}{\lambda}$ to have $k$ random arrivals, for $\lambda$=$\frac {k}{time\;length}$. So, it holds to say that the adjacent two events of random arrival would just take time $\frac {1}{\lambda}$, which is the ideal inter-arrival times.
➃each distinct inter-arrival times could then be modelled by random variable distributed in exponential probability.
➄the joint distribution of random arrivals would be modelled by gamma distribution.
➅the Poisson process has $n$ random arrivals in time interval $[a,b]$, the locations of these points are independent distributed, and each of them has a uniform distribution.
[2]
the exponential distribution
➀suppose $X$ is the rate of event occurrences during time period $t$.
➁suppose $V$ is the space where events take place within, then the success probability over time period $t$ is $\underset{Succss}P$=$\frac {X\cdot t}{V}$, and the failure probability is $\underset{Fail}P$=$1$-$\frac {X\cdot t}{V}$.
➂we divide time period $t$ by $n$, where $n\rightarrow\infty$, then success probability over time period $t$ becomes $\underset{Succss}P$=$\frac {X\cdot t}{V\cdot n}$, and the failure probability becomes $\underset{Fail}P$=$1$-$\frac {X\cdot t}{V\cdot n}$.
After time period $t$, what is the probability for no event occurrence? Equivalently, it is asking the probability for the very first event taking place after time period $t$.
➃This presumes that each subinterval $\frac {t}{n}$ is a failure case of the event, then:
$P(T>t)$
=$\lim_{n\rightarrow\infty}(\underset{Fail}P)^{n}$
=$\lim_{n\rightarrow\infty}(1-\frac {X\cdot t}{V\cdot n})^{n}$
$\approx e^{-\frac {X\cdot t}{V}}$
➄the success probability within time period $t$ could be expressed:
$\underset{Succss}P$=$1$-$e^{-\frac {X\cdot t}{V}}$=$P(T\le t)$
➅take $\lambda$=$\frac {X}{V}$, then, $P(T\le t)$=$1$-$e^{-\lambda\cdot t}$
$f_{T}(t)$=$D_{t}(1-e^{-\lambda\cdot t})$=$\lambda\cdot e^{-\lambda\cdot t}$
, where $\lambda$ is the intensity, the rate of success, or of event occurrence.
Example: Illustration Of The Similarities And Differences
[1]
Given the vehicles pass through a highway toll station is $6$ per minute, what is the probability that no cars within $30$ seconds?
➀by exponential distribution, we take $\lambda$=$6$ ($\frac {vehicles}{1\;minute}$), its PDF is $f_{exp}(t)$=$6\cdot e^{-6\cdot t}$, where $t>0$.
No cars within $30$ seconds asks for no car within $0.5$ minute, and we are figuring out the probability that $t>0.5$ will we just have the very first car come in, then:
$F_{exp}(t>0.5)$
=$\int_{0.5}^{\infty}6\cdot e^{-6\cdot t}\operatorname dt$
=$-e^{-6\cdot t}\vert_{0.5}^{\infty}$
=$e^{-3}$
➁by Poisson distribution, we can still use $\lambda$=$6$ ($\frac {vehicles}{1\;minute}$), its PDF is $f_{Pois}(x,t)$=$\frac {(6\cdot t)^{x}}{x!}\cdot e^{-6\cdot t}$, $t$ is now $0.5$.
Therefore, $f_{Pois}(0,0.5)$=$\frac {(6\cdot 0.5)^{0}}{0!}\cdot e^{-6\cdot 0.5}$=$e^{-3}$
We have found that the probability for no vehicles within the dedicated time interval is the same in both exponential and Poisson distribution. This is fully compliant with the claim that the very first inter-arrival times is itself an exponential distribution in Introduction To The Poisson Process Inter-arrival Times.
[2]
Still using the same rate that $6$ vehicles pass through a highway toll station per minute, then, what is the probability that all 6 cars crossing the toll station within 30 seconds?
➀from exponential distribution view point, this is asking the success probability within 30 seconds.
$F_{exp}(0.5)$
=$P_{exp}(t\le 0.5)$
=$\int_{0}^{0.5}6\cdot e^{-6\cdot t}\operatorname dt$
=$1$-$e^{-6\cdot 0.5}$=$0.950$
➁for Poisson distribution, this is to calculate the probability of distribution on the number $6$, which is the number of the requested target crossing vehicle counts within $0.5$ minute.
$P_{Pois}(x)$=$\frac {(\lambda\cdot t)^{x}}{x!}\cdot e^{-\lambda\cdot t}$…the Poisson PMF.
Now $t$=$0.5$, $x$=$6$, $P_{Pois}(6)$=$\frac {3^6}{6!}\cdot e^{-3}$=$0.168$
[Notes]
Why at this moment, the Poisson and exponential probability come out with different result?
➀as a result of the fact that we treat the pass probability as a whole by integration from each distinct exponential probability from $t$=$0$ to $t$=$0.5$, whereas we only calculate the Poisson probability distributed on the number $6$.
➁if we accumulate the distinct Poisson probability distributed on the numbers from $0$ to $6$, that is $\sum_{x=0}^{6}\frac {(\lambda\cdot t)^{x}}{x!}\cdot e^{-\lambda\cdot t}$, in this example, we get the probability $0.96649146…$, and the bias of $0.01$ could then be found.
By accumulating the distinct Poisson probability distribution from $0$ to $6$ is just to answer different question asking the probability of the number of cars passing by up to 6.
Example: Illustration Of Random Arrivals
[1]
Still using the same intensity, the rate that $6$ vehicles pass through a highway toll station per minute, then, what's the probability of the $8$-th vehicle passing through the toll station?
➀random arrivals doesn't reinforce the occurrence of specific event at dedicated time interval, in distinct time interval unit with regard to the given rate, which is $\frac {1}{rate}$, event outcome might just be true or false. Then, the k-th car should pass by after time length of $k\cdot\frac {1}{rate}$, if all goes well, just right at the k-th moment.
➁this involves the distribution of inter-arrival times, which is in exponential distribution itself, and the accumulation of which would leads to the gamma distribution, see Introduction To The Poisson Process Inter-arrival Times.
➂in this question, the most beautiful k-th random arrival takes place at the k-th moment of time interval unit. We need to transform the correct interval unit from the reciprocal value of the given rate.
The time interval unit would be $\frac {1}{\lambda}$. The k-th random arrival takes place at the k-th time interval unit, $\frac {k}{\lambda}$, in this example is $\frac {8}{6}$.
➃we have already proved that $f_{X_{n}}(t)$=$\frac {\lambda\cdot(\lambda\cdot t)^{n-1}\cdot e^{-\lambda\cdot t}}{(n-1)!}$, for $n$=$1$,$2$,..., where $\Gamma(n)$=$(n-1)!$. Then the probability of the 8-th vehicle passing through the toll station at the 8-th time interval unit would be calculated in this way.
$f_{X_{8}}(\frac {8}{6})$
=$\frac {6\cdot(6\cdot \frac {8}{6})^{7}\cdot e^{-6\cdot \frac {8}{6}}}{(7)!}$
=$0.8375191$
[2]
What is the probability of the $8$-th, $12$-th, $16$-th car passing by at the $3$-rd time interval unit?
➀$f_{X_{8}}(\frac {3}{6})$
=$\frac {6\cdot(6\cdot \frac {3}{6})^{7}\cdot e^{-6\cdot \frac {3}{6}}}{(7)!}$
=$0.12962418871490290869$
➁$f_{X_{12}}(\frac {3}{6})$
=$\frac {6\cdot(6\cdot \frac {3}{6})^{11}\cdot e^{-6\cdot \frac {3}{6}}}{(11)!}$
=$0.00132570193003877975$
➂$f_{X_{16}}(\frac {3}{6})$
=$\frac {6\cdot(6\cdot \frac {3}{6})^{15}\cdot e^{-6\cdot \frac {3}{6}}}{(15)!}$
=$0.00000327783444240358$
We can easily tell, the arrivals in the time interval unit of the order less than it, the probability would just decrease almost to $0$ as the order of arrival increases.
[3]
What is the probability of the $5$-th, $4$-th car passing by at the $5$-th, $4$-th time interval unit?
➀$f_{X_{5}}(\frac {5}{6})$
=$\frac {6\cdot(6\cdot \frac {5}{6})^{4}\cdot e^{-6\cdot \frac {5}{6}}}{(4)!}$
=$1.05280421860710423385$
➁$f_{X_{4}}(\frac {4}{6})$
=$\frac {6\cdot(6\cdot \frac {4}{6})^{3}\cdot e^{-6\cdot \frac {4}{6}}}{(3)!}$
=$1.1722008888789875388$
There exists no probability larger than $1.0$, above answer from gamma PDF just guarantees that $5$-th, $4$-th car passing by at the $5$-th, $4$-th time interval unit would definitely happen.
[4]
All we have done is by assuming that each i-th event arrival occurrs at the i-th time interval unit, this is not the normal case!!!
➀we can have a more random question about the probability of $10$-th car passing by after 10 minutes.
$f_{X_{10}}(10)$
=$\frac {6\cdot(6\cdot 10)^{9}\cdot e^{-6\cdot 10}}{(9)!}$
=$0.00000000000000145908$
This is quiet small probability for the $10$-th car passing by after 10 minutes, given that 6 cars would just across every one minute is the constant rate.
➁we then regularize the question by the probability of $60$-th car passing by after 10 minutes.
$f_{X_{60}}(10)$
=$\frac {6\cdot(6\cdot 10)^{59}\cdot e^{-6\cdot 10}}{(59)!}$
=$0.30859046994207513678$
This is a much higher probability than the probability for $10$-th car passing by after 10 minutes.
➁we then ask the question by the probability of $59$-th car passing by after 10 minutes.
$f_{X_{59}}(10)$
=$\frac {6\cdot(6\cdot 10)^{58}\cdot e^{-6\cdot 10}}{(58)!}$
=$0.30344729544304055116$
It’s a little smaller.
➂we then ask the question by the probability of $25$-th car passing by after 10 minutes.
$f_{X_{25}}(10)$
=$\frac {6\cdot(6\cdot 10)^{24}\cdot e^{-6\cdot 10}}{(24)!}$
=$0.00000040124226676254$
It’s much smaller.
As we can tell that the most optimized probability of random arrival by means of the gamma distribution would be the order of arrival is in 100 percent proportional to the time length it takes, given that the rate is a constant over time!!
➃soon we verify it with the case the $25$-th arrival at $25$-th time interval unit, that is
$f_{X_{25}}(\frac {25}{6})$
=$\frac {6\cdot(6\cdot \frac {25}{6})^{24}\cdot e^{-6\cdot \frac {25}{6}}}{(24)!}$
=$0.4771377088083926763$
Next, compare it with the $15$-th arrival at $25$-th time interval unit, that is
$f_{X_{15}}(\frac {25}{6})$
=$\frac {6\cdot(6\cdot \frac {25}{6})^{14}\cdot e^{-6\cdot \frac {25}{6}}}{(14)!}$
=$0.03560745811847304799$
Here we concrete above conclusion.
[5]
We are here with below probability as a summary
for the final finding.
$f_{X_{8}}(\frac {8}{6})$=$0.8375191$
$f_{X_{25}}(\frac {25}{6})$=$0.4771377088083926763$
$f_{X_{60}}(10)$=$0.30859046994207513678$, where $10$=$\frac {60}{6}$
As the event arrives at the time interval unit of appropriate proportion, which is also more closed to $1$, like $\frac {8}{6}$, it will just have higher probability by using the gamma distribution for a prediction.

 This is the case where $\lambda$=$\frac {k}{time\;length}$.
This is the case where $\lambda$=$\frac {k}{time\;length}$.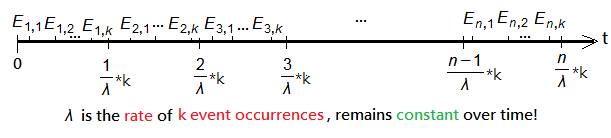 ➂it takes up time length of $\frac {k}{\lambda}$ to have $k$ random arrivals, for $\lambda$=$\frac {k}{time\;length}$. So, it holds to say that the adjacent two events of random arrival would just take time $\frac {1}{\lambda}$, which is the ideal inter-arrival times.
➂it takes up time length of $\frac {k}{\lambda}$ to have $k$ random arrivals, for $\lambda$=$\frac {k}{time\;length}$. So, it holds to say that the adjacent two events of random arrival would just take time $\frac {1}{\lambda}$, which is the ideal inter-arrival times.