05 Jan 2018
Prologue To The F Distribution
In probability theory and statistics, base on the most fundamental gamma distribution, F distribution is one of the many models of distributions further developed, furthermore, its definition is based on the chi-square distribution.
With the basic realization of gamma, chi-square distributions, we could also treat the F distribution a special case of the gamma distribution.
It would be greatly helpful in the evaluation of the regression model build on your hypothesis, the power of test for the precision in the machine learning results.
From The Chi-Square Distribution To The F Distribution
The model of F distribution is defined by the combination of two chi-square in ratio expression.
➀the definition is given by:
$F$=$\frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2}$, where $\chi_{\nu_i}^2$ is the chi-square PDF of DOF(degree of freedom) $\nu_i$, for $i=1,2$.
➁the F distribution PDF is expressed in below equality:
$h(f)$=$\frac {\Gamma(\frac {\nu_1+\nu_2}{2})\cdot (\frac {\nu_1}{\nu_2})^{\frac {\nu_1}{2}}}{\Gamma(\frac {\nu_1}{2})\cdot\Gamma(\frac {\nu_2}{2})}\cdot\frac {f^{\frac {\nu_1}{2}-1}}{(1+\frac {\nu_1}{\nu_2}\cdot f)^{\frac {\nu_1+\nu_2}{2}}}$
In the next paragraph, this article would prove ➁ by means of the joint probability density function in conjunction with the integration by part.
The F Distribution And The Joint PDF
This section would like to detail the joint PDF for the F distribution model.
➀suppose $X$, $Y$ are two independent random variables with PDF $f_X(x)$, $f_Y(y)$.
➁let $Z$=$\frac {Y}{X}$, we denote $f_{XY}(x,y)$ to be the PDF of $Z$, where it is also a random variable. Then for all $x\in X$, $y\in Y$, $z\in Z$, we have it that:
$P(\frac {y}{x}\le z)$=$P(y\le z\cdot x)$
Therefore, $F_{XY}(z)$=$\int_0^{\infty}\int_{-\infty}^{z\cdot x}f_{XY}(x,y)\operatorname dy\operatorname dx$
, well, we can treat $Y\in \chi_{\nu_1}^2$, $X\in \chi_{\nu_2}^2$ by intuition, and $F_{XY}(z)$ is the CDF(cumulative distribution function).
➂let $y$=$x\cdot v$, then, $\operatorname dy$=$x\cdot\operatorname dv$, this is a little utilization of integration by part.
$F_{XY}(z)$=$\int_0^{\infty}\int_{-\infty}^{z}x\cdot f_{XY}(x,y)\operatorname dv\operatorname dx$
$\;\;\;\;\;\;\;\;$=$\int_{-\infty}^{z}\int_0^{\infty}x\cdot f_{XY}(x,y)\operatorname dx\operatorname dv$
➃derivate $F_{XY}(z)$ with respect to $v$, would we eliminate the term $\operatorname dv$, and express $f_{XY}(z)$, the PDF of F only in one term of $x$.
$f_{XY}(z)$=$\frac {\operatorname dF_{XY}(z)}{\operatorname dv}$
$\;\;\;\;\;\;\;\;$=$\int_0^{\infty}x\cdot f_{XY}(x,y)\operatorname dx$
$\;\;\;\;\;\;\;\;$=$\int_0^{\infty}x\cdot f_{XY}(x,x\cdot z)\operatorname dx$…take $v=z$
$\;\;\;\;\;\;\;\;$=$\int_0^{\infty}x\cdot f_{X}\cdot f_{Y}(x\cdot z)\operatorname dx$
➄let $X$, $Y$ now be the random variables in chi-square PDF with DOF=$n$, $m$ respectively, and recall that $Z$=$\frac {Y}{X}$, then:
$f_Z(z)$=$\int_0^{\infty}x\cdot\frac {x^{\frac {n}{2}-1}\cdot e^{-\frac {x}{2}}}{2^{\frac {n}{2}}\cdot\Gamma(\frac {n}{2})}\cdot\frac {(x\cdot z)^{\frac {m}{2}-1}\cdot e^{-\frac {x\cdot z}{2}}}{2^{\frac {m}{2}}\cdot\Gamma(\frac {m}{2})}\operatorname dx$
$\;\;\;\;\;\;\;\;$=$\frac {z^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}x^{\frac{m+n}{2}-1}\cdot e^{-\frac {x\cdot(z+1)}{2}}\operatorname dx$
➅let $t$=$\frac {x\cdot(z+1)}{2}$, then $\operatorname dt$=$\frac {z+1}{2}\cdot \operatorname dx$, and $x$=$\frac {2\cdot t}{z+1}$
$f_Z(z)$=$\frac {z^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}(\frac {2\cdot t}{z+1})^{\frac{m+n}{2}-1}\cdot e^{-t}\cdot\frac {2}{z+1}\operatorname dt$
$\;\;\;\;\;\;\;\;$=$\frac {z^{\frac {m}{2}-1}\cdot(\frac {2}{z+1})^{\frac {m+n}{2}}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}t^{\frac{m+n}{2}-1}\cdot e^{-t}\operatorname dt$
$\;\;\;\;\;\;\;\;$=$\frac {z^{\frac {m}{2}-1}\cdot\Gamma(\frac {m+n}{2})}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot (z+1)^{\frac {m+n}{2}}}$
The F Distribution PDF Deduction
Above section, ➅ leaves a useful expression of joint PDF of two chi-square in the form $Z$=$\frac {Y}{X}$, inheriting from it, we will continue to deduce it out for the Z distribution PDF.
➀let $Z$=$\frac {Y}{m}/\frac {X}{n}$ to meet F distribution definition, then for all $x\in X$, $y\in Y$, $z\in Z$, we have:
$z$=$\frac {y}{x}\cdot\frac {n}{m}$, $y$=$\frac {m}{n}\cdot x\cdot z$
➁this time, let $y$=$\frac {m}{n}\cdot x\cdot v$, then, $\operatorname dy$=$\frac {m}{n}x\cdot\operatorname dv$:
$F_{XY}(z)$=$\int_{-\infty}^{z}\int_0^{\infty}\frac {m}{n}\cdot x\cdot f_{XY}(x,y)\operatorname dx\operatorname dv$
➂Differentiate $F_{XY}(z)$ by $\operatorname dv$:
$f_{XY}(z)$=$\frac {\operatorname dF_{XY}(z)}{\operatorname dv}$
$\;\;\;\;\;\;\;\;$=$\frac {m}{n}\int_0^{\infty}x\cdot f_{XY}(x,\frac {m}{n}\cdot x\cdot z)\operatorname dx$…take $v=z$
$\;\;\;\;\;\;\;\;$=$\frac {m}{n}\int_0^{\infty}x\cdot f_{X}\cdot f_{Y}(\frac {m}{n}\cdot x\cdot z)\operatorname dx$
…replace $x\cdot z$ by $\frac {m}{n}\cdot x\cdot z$
➃because $f_Z(z)$=$f_{XY}(z)$, now we have it that:
$f_Z(z)$=$\frac {m}{n}\int_0^{\infty}x\cdot\frac {x^{\frac {n}{2}-1}\cdot e^{-\frac {x}{2}}}{2^{\frac {n}{2}}\cdot\Gamma(\frac {n}{2})}\cdot\frac {(\frac {m}{n}\cdot x\cdot z)^{\frac {m}{2}-1}\cdot e^{-\frac {\frac {m}{n}\cdot x\cdot z}{2}}}{2^{\frac {m}{2}}\cdot\Gamma(\frac {m}{2})}\operatorname dx$
$\;\;\;\;\;\;\;\;$=$\frac {\frac {m}{n}\cdot(\frac {m}{n}\cdot z)^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}x^{\frac{m+n}{2}-1}\cdot e^{-\frac {x}{2}\cdot(\frac {m}{m}\cdot z+1)}\operatorname dx$
➄let $t$=$\frac {x}{2}\cdot(\frac {m}{m}\cdot z+1)$, then we have it that:
$x$=$\frac {2\cdot t}{\frac {m}{n}\cdot z+1}$, $\operatorname dx$=$\frac {2\cdot t}{\frac {m}{n}\cdot z+1}\cdot\operatorname dt$
$f_Z(z)$=$\frac {\frac {m}{n}\cdot(\frac {m}{n}\cdot z)^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot\int_0^{\infty}(\frac {2\cdot t}{\frac {m}{n}\cdot z+1})^{\frac{m+n}{2}-1}\cdot e^{-t}\frac {2\cdot t}{\frac {m}{n}\cdot z+1}\cdot\operatorname dt$
$\;\;\;\;\;\;\;\;$=$\frac {\frac {m}{n}\cdot(\frac {m}{n}\cdot z)^{\frac {m}{2}-1}}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot 2^{\frac {m+n}{2}}}\cdot(\frac {2}{\frac {m}{n}\cdot z+1})^{\frac{m+n}{2}}\cdot\int_0^{\infty}t^{\frac {m+n}{2}-1}\cdot e^{-t}\frac {2\cdot t}{\frac {m}{n}\cdot z+1}\cdot\operatorname dt$
$\;\;\;\;\;\;\;\;$=$\frac {\frac {m}{n}\cdot(\frac {m}{n}\cdot z)^{\frac {m}{2}-1}\cdot\Gamma(\frac {m+n}{2})}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot(\frac {m}{n}\cdot z+1)^{\frac{m+n}{2}}}$
$\;\;\;\;\;\;\;\;$=$\frac {(\frac {m}{n})^{\frac {m}{2}}\cdot z^{\frac {m}{2}-1}\cdot\Gamma(\frac {m+n}{2})}{\Gamma(\frac {m}{2})\cdot\Gamma(\frac {n}{2})\cdot(\frac {m}{n}\cdot z+1)^{\frac{m+n}{2}}}$
, where $X$, $Y$ are the random variables in chi-square PDF with DOF=$n$, $m$ respectively, and recall that $Z$=$\frac {Y}{m}/\frac {X}{n}$
The F Distribution Features
➀$f(\nu_1,\nu_2)$=$\frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2}$=$1/\frac {\frac {\chi_{\nu_2}^2}{\nu_2}}{\frac {\chi_{\nu_1}^2}{\nu_1}}$=$\frac {1}{f(\nu_2,\nu_1)}$
➁$f_{1-\alpha}(\nu_2,\nu_1)$=$\frac {1}{f_{\alpha}(\nu_1,\nu_2)}$, let’s see why.
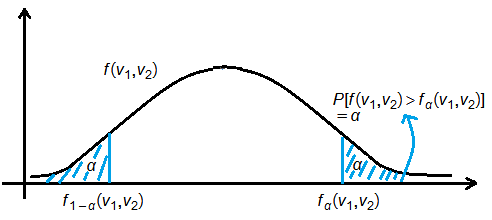
$\Rightarrow P\lbrack f(\nu_1,\nu_2)<f_\alpha(\nu_1,\nu_2)\rbrack$=$1-\alpha$
$\Rightarrow P\lbrack \frac {1}{f(\nu_2,\nu_1)}<f_\alpha(\nu_1,\nu_2)\rbrack$=$1-\alpha$
$\Rightarrow P\lbrack \frac {1}{f_\alpha(\nu_1,\nu_2)}<f(\nu_2,\nu_1)\rbrack$=$1-\alpha$
$\Leftrightarrow P\lbrack f(\nu_2,\nu_1)>f_{1-\alpha}(\nu_2,\nu_1)\rbrack$=$1-\alpha$
therefore, we have $f_{1-\alpha}(\nu_2,\nu_1)$=$\frac {1}{f_\alpha(\nu_1,\nu_2)}$
Expect Value Of The F Distribution
By definition, $F$=$\frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2}$
➀for all $f \in F$, to ask for its expect value:
$E\lbrack f\rbrack$=$E\lbrack \frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2}\rbrack$
$\;\;\;\;\;\;$=$\frac {\nu_2}{\nu_1}\cdot E\lbrack \frac {\chi_{\nu_1}^2}{\chi_{\nu_2}^2}\rbrack$
$\;\;\;\;\;\;$=$\frac {\nu_2}{\nu_1}\cdot E\lbrack \chi_{\nu_1}^2\rbrack\cdot E\lbrack \frac {1}{\chi_{\nu_2}^2}\rbrack$
, where we have $E\lbrack \chi_{\nu_1}^2\rbrack$=$\nu_1$, next for $E\lbrack \frac {1}{\chi_{\nu_2}^2}\rbrack$.
➁for all $x \in \chi_{\nu_2}^2$,
$E\lbrack \frac {1}{\chi_{\nu_2}^2}\rbrack$=$\int_0^{\infty}\frac {1}{x}\cdot\frac {x^{\frac {\nu_2}{2}-1}\cdot e^{-\frac {x}{\beta}}}{\beta^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\operatorname dx$
$\;\;\;\;\;\;$=$\int_0^{\infty}\frac {1}{x}\cdot\frac {x^{\frac {\nu_2}{2}-1}\cdot e^{-\frac {x}{2}}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\operatorname dx$, where $\beta$=$2$
➂to eliminate the complexity and try to express in terms of $\Gamma(\alpha)$,
let $y$=$\frac {x}{2}$, then we have $2\cdot\operatorname dy$=$\operatorname dx$,
$\Rightarrow\int_0^{\infty}\frac {1}{2\cdot y}\cdot\frac {(2\cdot y)^{\frac {\nu_2}{2}-1}\cdot e^{-\frac {x}{2}}\cdot 2}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\operatorname dy$
$=\frac {2^{\frac {\nu_2}{2}-1}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\int_0^{\infty}y^{(\frac {\nu_2}{2}-1)-1}\cdot e^{-y}\operatorname dy$
$=\frac {1}{2\cdot\Gamma(\frac {\nu_2}{2})}\cdot\Gamma(\frac {\nu_2}{2}-1)$
$=\frac {\Gamma(\frac {\nu_2}{2}-1)}{2\cdot(\frac {\nu_2}{2}-1)\cdot\Gamma(\frac {\nu_2}{2}-1)}$
$=\frac {1}{\nu_2-2}$
Therefore, $E\lbrack f\rbrack$=$\frac {\nu_2}{\nu_1}\cdot\nu_1\cdot\frac {1}{\nu_2-2}$=$\frac {\nu_2}{\nu_2-2}$
Moments Of The F Distribution
Before the variance of F distribution, by using the k-th ordinary moment could we speed up and be recalled that we have used it in the article of chi-square distribution.
➀for all $x \in \chi_{\nu_2}^2$
$E_r\lbrack\frac {1}{\chi_{\nu_2}^2}\rbrack$=$\int_0^{\infty}\frac {1}{x^r}\cdot\frac {x^{\frac {\nu_2}{2}-1}\cdot e^{-\frac {x}{2}}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\operatorname dx$
➁let $y$=$\frac {x}{2}$, then $x$=$2\cdot y$, $\operatorname dx=2\cdot\operatorname dy$
$\Rightarrow\int_0^{\infty}\frac {1}{(2\cdot y)^r}\cdot\frac {(2\cdot y)^{\frac {\nu_2}{2}-1}\cdot e^{-y}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\cdot 2\cdot\operatorname dy$
$=\frac {2\cdot 2^{-r}\cdot 2^{\frac {\nu_2}{2}-1}}{2^{\frac {\nu_2}{2}}\cdot\Gamma(\frac {\nu_2}{2})}\cdot\int_0^{\infty}y^{-r}\cdot y^{\frac {\nu_2}{2}-1}\cdot e^{-y}\operatorname dy$
$=\frac {2^{-r}}{\Gamma(\frac {\nu_2}{2})}\cdot\int_0^{\infty}y^{\frac {\nu_2}{2}-r-1}\cdot e^{-y}\operatorname dy$
$=\frac {2^{-r}}{\Gamma(\frac {\nu_2}{2})}\cdot\Gamma(\frac {\nu_2}{2}-r)$
➂for $r=1$, $\mu_1$, we have it that:
$E_1\lbrack\frac {1}{\chi_{\nu_2}^2}\rbrack$
$=\mu_1$
$=\frac {2^{-1}}{\Gamma(\frac {\nu_2}{2})}\cdot\Gamma(\frac {\nu_2}{2}-1)$
$=\frac {2^{-1}}{(\frac {\nu_2}{2}-1)\cdot\Gamma(\frac {\nu_2}{2}-1)}\cdot\Gamma(\frac {\nu_2}{2}-1)$
$=\frac {1}{\nu_2-2}$
➃for $r=2$, $\mu_2$, we have it that:
$E_2\lbrack\frac {1}{\chi_{\nu_2}^2}\rbrack$
$=\mu_2$
$=\frac {2^{-2}}{\Gamma(\frac {\nu_2}{2})}\cdot\Gamma(\frac {\nu_2}{2}-2)$
$=\frac {2^{-2}}{(\frac {\nu_2}{2}-1)\cdot(\frac {\nu_2}{2}-2)\cdot\Gamma(\frac {\nu_2}{2}-2)}\cdot\Gamma(\frac {\nu_2}{2}-2)$
$=\frac {1}{2^2\cdot\frac {\nu_2-2}{2})\cdot(\frac {\nu_2-4}{2})}$
$=\frac {1}{(\nu_2-2)\cdot(\nu_2-4)}$
Variance Of The F Distribution
Succeeding to results of moments from above paragraph, we proceed to ask for the variance of F distribution. Please recall that we have the 2nd ordinary moment of the chi-square $E_2\lbrack(\chi_{\nu}^2)^2\rbrack=\nu^2+2\cdot\nu$.
➀$Var\lbrack f\rbrack$=$E\lbrack f^2\rbrack$-$E^2\lbrack f\rbrack$, next to figure out $E\lbrack f^2\rbrack$
$E\lbrack f^2\rbrack$
$=E\lbrack (\frac {\chi_{\nu_1}^2}{\nu_1}/\frac {\chi_{\nu_2}^2}{\nu_2})^2\rbrack$
$=(\frac {\nu_2}{\nu_1})^2\cdot E\lbrack (\frac {\chi_{\nu_1}^2}{\chi_{\nu_2}^2})^2\rbrack$
$=(\frac {\nu_2}{\nu_1})^2\cdot E\lbrack (\chi_{\nu_1}^2)^2\rbrack\cdot E\lbrack (\frac {1}{\chi_{\nu_2}^2})^2\rbrack$
$=(\frac {\nu_2}{\nu_1})^2\cdot(\nu_1^2+2\cdot\nu_1)\cdot\frac {1}{(\nu_2-2)\cdot(\nu_2-4)}$
$=\frac {\nu_2^2}{\nu_1}\cdot(\nu_1+2)\cdot\frac {1}{(\nu_2-2)\cdot(\nu_2-4)}$
➁therefore, the variance could now be expressed:
$Var\lbrack f\rbrack$
$=E\lbrack f^2\rbrack$-$E^2\lbrack f\rbrack$
$=\frac {\nu_2^2}{\nu_1}\cdot(\nu_1+2)\cdot\frac {1}{(\nu_2-2)\cdot(\nu_2-4)}$-$(\frac {\nu_2}{\nu_2-2})^2$
$=\frac {\nu_2^2\cdot(\nu_1+2)\cdot(\nu_2-2)}{\nu_1\cdot(\nu_2-2)^2\cdot(\nu_2-4)}$-$\frac {\nu_1\cdot\nu_2^2\cdot(\nu_2-4)}{\nu_1\cdot(\nu_2-2)^2\cdot(\nu_2-4)}$
$=\frac {2\cdot\nu_2^2\cdot(\nu_1+\nu_2-2)}{\nu_1\cdot(\nu_2-2)^2\cdot(\nu_2-4)}$
, where $\nu_2>4$ is the condition, it must hold!!!
03 Jan 2018
Prologue To The Chi-Square Distribution
In probability theory and statistics, base on the most fundamental gamma distribution, one of the many models of distributions further developed is the chi-square distribution.
With the basic realization of gamma distribution, we can treat the chi-square distribution a special case of the gamma distribution.
It would be greatly helpful in the evaluation of the regression model build on your hypothesis, the power of test for the precision in the machine learning results.
From The Gamma Distribution To The Chi-Square Distribution
Be recalled that we have gamma function and the PDF of the gamma distribution:
➀$\Gamma(\alpha)$=$\int_0^\infty x^{\alpha-1}\cdot e^{-x}\operatorname dx$, where $\alpha>0$.
➁$f(x)=\frac {1}{\beta^{\alpha}\cdot\Gamma(\alpha)}\cdot x^{\alpha-1}\cdot e^{-\frac{x}{\beta}}$, where $\alpha>0$, $\beta>0$
Next, we take $\alpha=\frac\nu2$, $\beta=2$, we turn the PDF function into below expression:
$f(x)=\frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot x^{\frac \nu2 -1}\cdot e^{-\frac {x}{2}}$, for $x>0$
, where $\nu$ is a positive integer, and this is the chi-square PDF.
It is just a special case of the gamma distribution with $\alpha=\frac\nu2$, $\beta=2$, and $\nu$ is the degree of freedom.
The Chi-Square Distribution Is Right-Skew
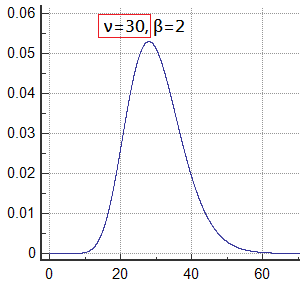
As degree of freedom increases, chi-square distribution would approximate the normal distribution.
You can easily see that as $\nu$ increases, the distribution of chi-square changes.
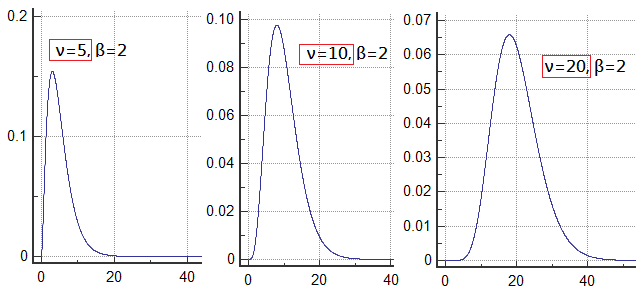 Gradually, it will approximate the normal distribution.
Gradually, it will approximate the normal distribution.
The Chi-Square And The MGF, Why?
Because by means of the moment, we can easily figure out the $E\lbrack X\rbrack$, $E\lbrack X^2\rbrack$, $E\lbrack X^3\rbrack$ with 1st, 2nd, 3rd order of differentiation.
➀we can formulate the MGF of chi-square in below expression:
$M_X(t)=\int_0^\infty e^{t\cdot x}\cdot \frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot x^{\frac \nu2 -1}\cdot e^{-\frac {x}{2}}\operatorname dx$
$\;\;\;\;\;\;=\int_0^\infty \frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot x^{\frac \nu2 -1}\cdot e^{-\frac {1}{2}\cdot (1-2\cdot t)\cdot x}\operatorname dx$
➁let $y=\frac {1}{2}\cdot (1-2\cdot t)\cdot x$
$\Rightarrow x=\frac {2\cdot y}{1-2\cdot t}$
$\Rightarrow \frac {\operatorname dx}{\operatorname dx}=\frac {2}{1-2\cdot t}\cdot\frac {\operatorname dy}{\operatorname dx}$
$\Rightarrow 1\cdot \operatorname dx=\frac {2}{1-2\cdot t}\cdot \operatorname dy$
$\Rightarrow \operatorname dx=\frac {2}{1-2\cdot t}\cdot \operatorname dy$
➂replace $\operatorname dx$ with $\frac {2}{1-2\cdot t}\cdot \operatorname dy$
$M_X(t)=\int_0^\infty \frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot (\frac {2\cdot y}{1-2\cdot t})^{\frac \nu2 -1}\cdot e^{-y}\cdot\frac {2}{1-2\cdot t}\cdot \operatorname dy$
$\;\;\;\;\;\;=\frac {1}{2^{\frac \nu2}\cdot\Gamma(\frac \nu2)}\cdot (\frac {2}{1-2\cdot t})^{\frac \nu2}\cdot\int_0^\infty y^{\frac \nu2 -1}\cdot e^{-y} \operatorname dy$
$\;\;\;\;\;\;=\frac {1}{2^{\frac \nu2}\cdot\Gamma(\frac \nu2)}\cdot (\frac {2}{1-2\cdot t})^{\frac \nu2}\cdot\Gamma(\frac \nu2)$
$\;\;\;\;\;\;=(\frac {1}{1-2\cdot t})^{\frac \nu2}$
$\;\;\;\;\;\;=(1-2\cdot t)^{-\frac \nu2}$
, where we have $\Gamma(\frac \nu2)$=$\int_0^\infty y^{\frac \nu2 -1}\cdot e^{-y} \operatorname dy$
Expect Value And Variance Of Chi-Square Distribution
Succeeding to above, we have deduce out the MGF of chi-square, we could just easily figure out the $\mu_1$, $\mu_2$:
$\mu_1$=$M_X^{′}(t)\vert_{t=0}$
$\;\;\;\;$=$\frac{\operatorname dM_X(t)}{\operatorname dt}\vert_{t=0}$
$\;\;\;\;$=$-\frac {\nu}{2}\cdot (1-2\cdot t)^{-\frac \nu2 -1}\cdot (-2)\vert_{t=0}$
$\;\;\;\;$=$\nu\cdot (1-2\cdot t)^{-\frac \nu2 -1}\vert_{t=0}$
$\;\;\;\;$=$\nu$=$E\lbrack X\rbrack$
$\mu_2$=$M_X^{″}(t)\vert_{t=0}$
$\;\;\;\;$=$\frac{\operatorname d^{2}M_X(t)}{\operatorname dt^{2}}\vert_{t=0}$
$\;\;\;\;$=$\nu\cdot (-\frac {\nu}{2}-1)\cdot (1-2\cdot t)^{-\frac \nu2 -2}\cdot (-2)\vert_{t=0}$
$\;\;\;\;$=$2\cdot\nu\cdot (\frac {\nu}{2}+1)\cdot (1-2\cdot t)^{-\frac \nu2 -2}\vert_{t=0}$
$\;\;\;\;$=$\nu^2+2\cdot\nu$=$E\lbrack X^2\rbrack$
Therefore, $Var\lbrack X\rbrack$=$E\lbrack X^2\rbrack-E^2\lbrack X\rbrack$=$2\cdot\nu$
$Z^2\sim\chi_1^2$
In this section, I’d like to prove that $Z^2\sim\chi_1^2$, it says that the squared standard normal distribution is similar or even approximate to the chi-square distribution.
Well, we denote $ɸ(0,1)$ to be the standard normal distribution with mean $0$ and variance $1$, and $\chi_i^2$ to stand for the chi-square distribution, with degree of freedom equal to $i$. If you see $\chi_1^2$, it means ch-square with degree of freedom $1$.
proof:
➀we’ll use Jacobian for the change of variable in this proof.
Given $x\in X$, $y\in Y$, $X$ and $Y$ are two random variables.
Suppose $f_X(x)$ is the PDF of $X$, and $f_Y(y)$ is the PDF of $Y$, then, below equality just holds.
$\int_0^\infty f_Y(y) \operatorname dy$=$1$=$\int_0^\infty f_X(x) \operatorname dx$
$\Rightarrow\frac {\operatorname d\int_0^\infty f_Y(y) \operatorname dy}{\operatorname dy}$=$\frac {\operatorname d\int_0^\infty f_X(x) \operatorname dx}{\operatorname dy}$
$\Rightarrow f_Y(y)$=$\frac {f_X(x)\operatorname dx}{\operatorname dy}$
$\Rightarrow f_Y(y)$=$f_X(x)\cdot\frac {\operatorname dx}{\operatorname dy}$
where we denote $J=\frac {\operatorname dx}{\operatorname dy}$
➁suppose the random variable $X$ is normal distributed with $\mu$ as its mean, and $\sigma^2$ as its variance, where we denote it $X\sim N(\mu,\sigma^2)$.
Suppose $Z$ is another random variable. If for all $z\in Z$, we take $z$=$\frac {x-\mu}{\sigma}$, then, $Z\sim ɸ(0,1)$ and below PDF of $Z$ just holds.
$f_Z(z)$=$\frac {1}{\sqrt{2\cdot\pi}}\cdot e^{-\frac{z^2}{2}}$
➂for all $y\in Y$, $z\in Z$, let $Y=Z^2$, then, $Z=\pm\sqrt Y$,
Further take $Z_1=-\sqrt Y$, $Z_2=\sqrt Y$, therefore, we have:
$\frac {\operatorname dz_1}{\operatorname dy}$=$-\frac {1}{2\cdot\sqrt y}$=$J_1$
$\frac {\operatorname dz_2}{\operatorname dy}$=$\frac {1}{2\cdot\sqrt y}$=$J_2$
➃we have $f_Y(y)$=$f_X(x)\cdot\frac {\operatorname dx}{\operatorname dy}$ in ➀ that we can now do the funny transform in between $Y$ and $Z$, to express $Y$ in terms of $Z_1$, $Z_2$.
$f_Y(y)$=$\frac {1}{\sqrt {2\cdot\pi}}\cdot e^{-\frac{y}{2}}\cdot\left|J_1\right|$+$\frac {1}{\sqrt {2\cdot\pi}}\cdot e^{-\frac{y}{2}}\cdot\left|J_2\right|$
$\;\;\;\;\;\;$=$\frac {1}{\sqrt {2\cdot\pi}}\cdot e^{-\frac{y}{2}}\cdot\left|-\frac {1}{2\cdot\sqrt y}\right|$+$\frac {1}{\sqrt {2\cdot\pi}}\cdot e^{-\frac{y}{2}}\cdot\left|\frac {1}{2\cdot\sqrt y}\right|$
$\;\;\;\;\;\;$=$\frac {1}{\sqrt {2\cdot\pi}}\cdot\frac {1}{\sqrt y}\cdot e^{-\frac{y}{2}}$
$\;\;\;\;\;\;$=$\frac {1}{\sqrt2\cdot\sqrt {\pi}}\cdot\frac {1}{\sqrt y}\cdot e^{-\frac{y}{2}}$
$\;\;\;\;\;\;$=$\frac {1}{2^{\frac {1}{2}}\cdot\sqrt {\pi}}\cdot y^{-\frac {1}{2}}\cdot e^{-\frac{y}{2}}$
$\;\;\;\;\;\;$=$\frac {1}{2^{\frac {1}{2}}\cdot\Gamma(\frac {1}{2})}\cdot y^{-\frac {1}{2}}\cdot e^{-\frac{y}{2}}$
➄we already know $\Gamma(\frac {1}{2})$=$\sqrt\pi$, this is quiet a beautiful deduction that it is just the PDF of gamma distribution with $\alpha=\frac {1}{2}$, $\beta=2$.
$\frac {1}{2^{\frac {1}{2}}\cdot\Gamma(\frac {1}{2})}\cdot y^{-\frac {1}{2}}\cdot e^{-\frac{y}{2}}$ is just the chi-square PDF, Guess what?
$f(x)=\frac {1}{2^{\frac \nu2}\cdot \Gamma(\frac \nu2)}\cdot x^{\frac \nu2 -1}\cdot e^{-\frac {x}{2}}$ with $\alpha=\frac {\nu}{2}$, $\nu=1$, $\beta=2$, for $x>0$.
Therefore, we just get $Z^2\sim\chi_1^2$ proved.
Sample Variance Evaluation Against Distribution Variance
Given $X_1$,$X_2$,$X_3$,…,$X_n\in N(\mu,\sigma^2)$, where each $X_i$ is an independent random variable, then:
$Z_i$=$\frac {X_i-\mu}{\sigma}$ is a standard normal distribution, $ɸ(0,1)$, for $i=1$ to $n$.
We have already proved $$Z^2\sim\chi_1^2$$, then, $$\sum_{i=1}^{n}Z_i^{2}\sim\chi_n^{2}$ could be obtained by mathematics induction. Suppose it is true and this proof would guide you through the relation in between sample variance and distribution variance.
proof:
➀expand from $Z_i^2$
$\sum_{i=1}^{n}Z_i^2$=$\sum_{i=1}^{n}(\frac {X_i-\mu}{\sigma})^2$
$\;\;\;\;\;\;\;\;$=$\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}+\overline{X_n}-\mu}{\sigma})^2$
$\;\;\;\;\;\;\;\;$=$\sum_{i=1}^{n}(\frac {(X_i-\overline{X_n})+(\overline{X_n}-\mu)}{\sigma})^2$
$\;\;\;\;\;\;\;\;$=$\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}}{\sigma})^2$+$\sum_{i=1}^{n}(\frac {\overline{X_n}-\mu}{\sigma})^2$+$2\cdot\sum_{i=1}^{n}\frac {(X_i-\overline{X_n})\cdot (\overline{X_n}-\mu)}{\sigma^2}$
, where $\overline{X_n}$ is the average for the whole $X_i’s$, for $i=1$ to $n$.
➁the final term is 0.
$\sum_{i=1}^{n}\frac {(X_i-\overline{X_n})\cdot (\overline{X_n}-\mu)}{\sigma^2}$
$=\frac {(\overline{X_n}-\mu)}{\sigma^2}\cdot\sum_{i=1}^{n}(X_i-\overline{X_n})=0$
Thus, we have it that:
$\sum_{i=1}^{n}Z_i^2$=$\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}}{\sigma})^2$+$\sum_{i=1}^{n}(\frac {\overline{X_n}-\mu}{\sigma})^2$
➂still focus on the final term.
$\sum_{i=1}^{n}(\frac {\overline{X_n}-\mu}{\sigma})^2$=$n\cdot (\frac {\overline{X_n}-\mu}{\sigma})^2$=$(\frac {\overline{X_n}-\mu}{\frac {\sigma}{\sqrt n}})^2$
Therefore, $\sum_{i=1}^{n}(\frac {\overline{X_n}-\mu}{\sigma})^2\approx Z_1^2\sim\chi_1^2$
Remember that we are under the assumption that $$\sum_{i=1}^{n}Z_i^{2}\sim\chi_n^{2}$ is true, then:
$\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}}{\sigma})^2+\chi_1^2\sim\chi_n^2$ must hold.
$\Rightarrow\sum_{i=1}^{n}(\frac {X_i-\overline{X_n}}{\sigma})^2\sim\chi_{n-1}^2$ must hold.
➃in statistics, we denote sample variance as $S^2$ and have it that:
$S^2$=$\sum \frac {(X_i-\overline{X_n})^2}{n-1}$
$\Rightarrow (n-1)\cdot S^2=\sum (X_i-\overline{X_n})^2$
Therefore, $\frac {(n-1)\cdot S^2}{\sigma^2}\sim\chi_{n-1}^2$ is the final deduction result.
We can conclude that sample variance tested against normal distribution variance follows the $\chi_{n-1}^{2}$ distribution, with the assumption that the random sample of size $n$ is from $N(\mu,\sigma^2)$.
At the end of this article, it would be trivial that $\chi_n^2$=$\chi_{n-1}^2$+$\chi_1^2$ just holds.
29 Dec 2017
Prologue To The Gamma Distribution
In probability theory and statistics, the gamma distribution is the most fundamental, which is based on for further development of many distributions, they are beta, exponential, F, chi-square, t distributions and still others.
With the basic intuition of gamma distribution would it be greatly helpful in the evaluation of the regression model build on your hypothesis, even more, the power of test for the precision in the machine learning results.
The Gamma Function $\Gamma$
It is very important in the gamma distribution, first of all, we take not only a glance over it, but go through some of the major properties of it. The gamma function comes in the definition:
$\Gamma(\alpha)$=$\int_0^\infty x^{\alpha-1}\cdot e^{-x}\operatorname dx$, where $\alpha>0$.
Taking advantage of integration by part:
Let $u=x^{\alpha-1}$, $\operatorname dv$=$e^{-x}\operatorname dx$, then,
$\operatorname du$=$(\alpha-1)\cdot x^{\alpha-2}$, $v$=$-e^{-x}$.
$\Gamma(\alpha)$=$x^{\alpha-1}\cdot(-e^{-x})\vert_0^\infty$-$\int_0^\infty -e^{-x}\cdot (\alpha-1)\cdot x^{\alpha-2}\operatorname dx$
$\;\;\;\;\;\;\;$=$0$+$\int_0^\infty e^{-x}\cdot (\alpha-1)\cdot x^{\alpha-2}\operatorname dx$
$\;\;\;\;\;\;\;$=$(\alpha-1)\cdot\int_0^\infty e^{-x}\cdot x^{\alpha-2}\operatorname dx$
$\;\;\;\;\;\;\;$=$(\alpha-1)\cdot\Gamma(\alpha-1)$
$\Gamma(5)=4\cdot\Gamma(4)$, therefore, we can deduce it out that:
$\Gamma(\alpha)$=$(\alpha-1)\cdot\Gamma(\alpha-1)$
$\;\;\;\;\;\;\;$=$(\alpha-1)\cdot(\alpha-2)\cdot\Gamma(\alpha-2)$=$\cdots$
[1]the corollary has it that:
$\Gamma(n)$=$(n-1)\cdot(n-2)\cdot(n-3)\cdots\Gamma(1)$
,where $\Gamma(1)$=$\int_0^\infty x^0\cdot e^{-x}\operatorname dx$=$-e^{-x}\vert_0^\infty$=$1$
, thus, $\Gamma(n)=(n-1)!$ is obtained.
[2]$\Gamma(\frac{1}{2})$=$\sqrt{\mathrm\pi}$
There exists some alternatives, either way could be:
proof::➀
As we don’t like $-\frac{1}{2}$, by means of change unit,
let $x$=$u^2$, then, $\operatorname dx$=$2\cdot u\operatorname du$:
$\Gamma(\frac{1}{2})$=$\int_0^\infty x^{-\frac{1}{2}}\cdot e^{-x}\operatorname dx$
$\;\;\;\;\;\;\;$=$\int_0^\infty u^{-1}\cdot e^{-u^{2}}\cdot 2\cdot u\operatorname du$
$\;\;\;\;\;\;\;$=$2\cdot\int_0^\infty e^{-u^{2}}\operatorname du$
Take $I$=$\int_0^\infty e^{-u^{2}}\operatorname du$, then,
$I^2$=$\int_0^\infty e^{-x^{2}}\operatorname dx$ $\int_0^\infty e^{-y^{2}}\operatorname dy$
$\;\;\;\;$=$\int_0^\infty\int_0^\infty e^{-(x^{2}+y^{2})}\operatorname dx\operatorname dy$
Guess what? We just transform our integral to the quadrant one.
Take $r^2$=$x^2$+$y^2$, we can have below two sets of deduction:
➀$\frac{\operatorname dr^2}{\operatorname dx}$=$\frac{\operatorname d(x^2+y^2)}{\operatorname dx}$=$2\cdot x$
$\Rightarrow\operatorname dr^2$=$2\cdot x\operatorname dx$
➁$\frac{\operatorname dr^2}{\operatorname dr}$=$\frac{\operatorname d(x^2+y^2)}{\operatorname dr}$
$\Rightarrow 2\cdot r$=$\frac{\operatorname d(x^2+y^2)}{\operatorname dr}$
$\Rightarrow 2\cdot r\operatorname dr$=$\operatorname d(x^2+y^2)$
$\Rightarrow 2\cdot r\frac{\operatorname dr}{\operatorname dx}$=$2\cdot x$
$\Rightarrow r\operatorname dr$=$x\operatorname dx$
Replace ➀ and ➁ in below integral:
$\int_0^\infty e^{-r^{2}}\operatorname dr^2$
$=\int_0^\infty e^{-r^{2}}\frac{\operatorname dr^2}{\operatorname dx}\cdot\operatorname dx$
$=\int_0^\infty e^{-r^{2}}\cdot 2\cdot x\operatorname dx$
$=\int_0^\infty \cdot 2\cdot r\cdot e^{-r^{2}}\operatorname dr$
$=-e^{r^{2}}\vert_0^\infty$
$=1$
Please recall that we have our integration area in quadrant one, at this moment, back to $I$, let $\theta=y$ to integrate from $0$ to $\frac{\pi}{2}$:
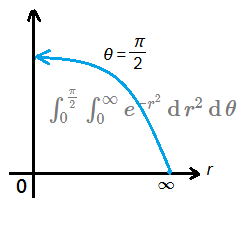 $I^2$=$\int_0^{\frac{\pi}{2}}\int_0^\infty e^{-r^{2}}\operatorname dr^2\operatorname d\theta$
$I^2$=$\int_0^{\frac{\pi}{2}}\int_0^\infty e^{-r^{2}}\operatorname dr^2\operatorname d\theta$
$\;\;\;\;$=$\int_0^{\frac{\pi}{2}}\operatorname d\theta$ $\int_0^\infty e^{-r^{2}}\cdot x\operatorname dx$
$\;\;\;\;$=$\frac{\pi}{2}$ $\int_0^\infty e^{-r^{2}}\cdot r\operatorname dr$
$\;\;\;\;$=$\frac{\pi}{2}\cdot(-\frac{1}{2}\cdot e^{-r^{2}})\vert_0^\infty$
$\;\;\;\;$=$\frac{\pi}{2}\cdot(0-\frac{1}{2})$
$\;\;\;\;$=$\frac{\pi}{4}$
$\Gamma(\frac{1}{2})$=$2\cdot\int_0^\infty e^{-u^{2}}\operatorname du$=$2\cdot I$, where $I$=$\int_0^\infty e^{-u^{2}}\operatorname du$ is something we have already known.
Therefore, $I^2$=$\frac{\pi}{4}$, and $I$=$\frac{\sqrt\pi}{2}$, finally, we have $\Gamma(\frac{1}{2})$=$\sqrt\pi$ thus proved.
proof::➁
$\Gamma(\frac{1}{2})$=$\int_0^\infty x^{-\frac{1}{2}}\cdot e^{-x}\operatorname dx$, here we are again.
Take $x$=$\frac {z^2}{2}$, then, $\frac {\operatorname dx}{\operatorname dz}$=$z$, thus, we have $\operatorname dx$=$z\operatorname dz$
$\int_0^\infty x^{-\frac{1}{2}}\cdot e^{-x}\operatorname dx$
$=\int_0^\infty (\frac {z^2}{2})^{-\frac{1}{2}}\cdot e^{-\frac {z^2}{2}}z\operatorname dz$
$=\int_0^\infty \sqrt2\cdot z^{-1}\cdot e^{-\frac {z^2}{2}}z\operatorname dz$
$=\sqrt2\int_0^\infty e^{-\frac {z^2}{2}}z\operatorname dz$
$=2\cdot\sqrt\pi\int_0^\infty \frac {1}{\sqrt{2\cdot\pi}}\cdot e^{-\frac {z^2}{2}}z\operatorname dz$
$=2\cdot\sqrt\pi\cdot\frac {1}{2}$
$=\sqrt\pi$
where $\int_{-\infty}^\infty \frac {1}{\sqrt{2\cdot\pi}}\cdot e^{-\frac {z^2}{2}}z\operatorname dz=1$ is the accumulative probability of normal distribution, therefore, $\int_0^\infty \frac {1}{\sqrt{2\cdot\pi}}\cdot e^{-\frac {z^2}{2}}z\operatorname dz=\frac {1}{2}$.
The PDF of Gamma Distribution
Next we inspect the PDF(probability density function) of the gamma distribution. The $f(x)$ of PDF is expressed as:
$f(x)=\frac {1}{\beta^{\alpha}\cdot\Gamma(\alpha)}\cdot x^{\alpha-1}\cdot e^{-\frac{x}{\beta}}$
$\;\;\;\;\;\;=\frac {1}{\beta\cdot\Gamma(\alpha)}\cdot (\frac{x}{\beta})^{\alpha-1}\cdot e^{-\frac{x}{\beta}}$
$\;\;\;\;\;\;=\frac {\frac {1}{\beta}\cdot(\frac{x}{\beta})^{\alpha-1}\cdot e^{-\frac{x}{\beta}}}{\Gamma(\alpha)}$
, where $\alpha>0$, $\beta>0$
By taking $\lambda=\frac{1}{\beta}$, then, we just have it that:
$f(x)=\frac {\lambda\cdot(\lambda\cdot x)^{\alpha-1}\cdot e^{-\lambda\cdot x}}{\Gamma(\alpha)}$
What do we mean by the parameters $\alpha$, $\beta$, $\lambda$?
➀$\alpha$ is for the sharpness of the distribution.
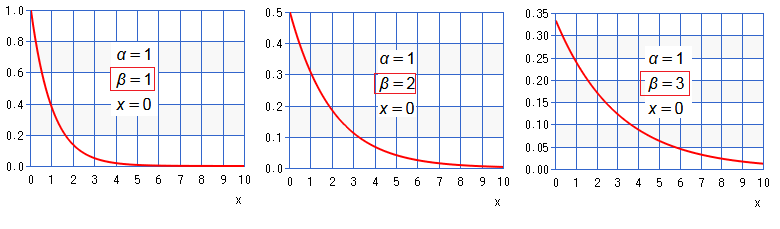
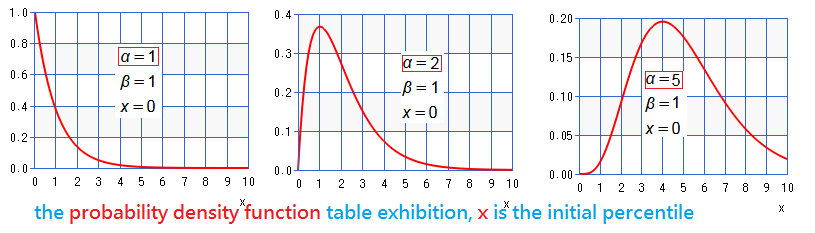 ➁the spread or dissemination of the distribution could be resort to $\beta$.
➁the spread or dissemination of the distribution could be resort to $\beta$.
 ➂$\lambda$ is for the intensity, that is, the rate, frequency, in the form of $\frac {count}{time unit}$.
➂$\lambda$ is for the intensity, that is, the rate, frequency, in the form of $\frac {count}{time unit}$.
Expect Value And Variance Of Gamma Distribution
As we know that it is the PDF of the gamma distribution:
$f(x)=\frac {1}{\beta^{\alpha}\cdot\Gamma(\alpha)}\cdot x^{\alpha-1}\cdot e^{-\frac{x}{\beta}}$
Next to figure out the expect value and variance of the gamma distribution. The suggestion would be made that we should take advantage of the moment in Introduction To The Moment Generating Function.
$E\lbrack X^k\rbrack$=$\frac{1}{\beta^{\alpha}\cdot\Gamma(\alpha)}\int_0^{\infty}x^{k}\cdot x^{\alpha-1}\cdot e^{-\frac{x}{\beta}}\operatorname dx$
Let $y=\frac{x}{\beta}$, and we can have, $\operatorname dy=\frac{1}{\beta}\operatorname dx$, then:
$E\lbrack X^k\rbrack$=$\frac{1}{\beta^{\alpha}\cdot\Gamma(\alpha)}\int_0^{\infty}x^{k+\alpha-1}\cdot e^{-\frac{x}{\beta}}\operatorname dx$
$\;\;\;\;\;\;\;\;=\frac{1}{\beta^{\alpha}\cdot\Gamma(\alpha)}\int_0^{\infty}(\beta\cdot y)^{k+\alpha-1}\cdot e^{-y}\cdot\beta\operatorname dy$
$\;\;\;\;\;\;\;\;=\frac{\beta^{k+\alpha-1}\cdot\beta}{\beta^{\alpha}\cdot\Gamma(\alpha)}\int_0^{\infty}(y)^{k+\alpha-1}\cdot e^{-y}\operatorname dy$
$\;\;\;\;\;\;\;\;=\frac{\beta^{k}}{\Gamma(\alpha)}\int_0^{\infty}(y)^{k+\alpha-1}\cdot e^{-y}\operatorname dy$
$\;\;\;\;\;\;\;\;=\frac{\beta^{k}}{\Gamma(\alpha)}\cdot\Gamma(k+\alpha)$
➀$E\lbrack X\rbrack$=$\mu_1$, the first ordinary moment, by taking $k=1$, we can have the expected value expressed as:
$E\lbrack X\rbrack$=$\frac{\beta}{\Gamma(\alpha)}\cdot\Gamma(1+\alpha)$=$\beta\cdot\alpha$
➁$Var\lbrack X\rbrack=E\lbrack X^2\rbrack-E^2\lbrack X\rbrack$, by taking $k=2$, we can obtain $E\lbrack X^2\rbrack$=$\mu_2$, the second ordinary moment, and have the expression of the variance:
$Var\lbrack X\rbrack$=$\frac{\beta^{2}}{\Gamma(\alpha)}\cdot\Gamma(2+\alpha)$-$(\beta\cdot\alpha)^2$
$\;\;\;\;\;\;=\beta^{2}\cdot(\alpha+1)\cdot(\alpha)$-$(\beta\cdot\alpha)^2$
$\;\;\;\;\;\;=\beta^2\cdot\alpha\cdot(\alpha-1-\alpha)$
$\;\;\;\;\;\;=\beta^2\cdot\alpha$
28 Dec 2017
Prologue To The Moment Generating Function
In probability theory and statistics, the moment generating function(MGF) of a real-valued random variable is an alternative specification of its probability distribution. Caution must be made that not all random variables
have moment generating functions. This article introduce to MGF with a hope that it could fasten the way to generalize the expectation and variance of a random variable with regards to its given PDF(contiguous) or PMF(discrete)
by means of moment.
What is a Moment?
The expected values $E\lbrack X\rbrack$, $E\lbrack X^2\rbrack$, $E\lbrack X^3\rbrack$,…, and $E\lbrack X^r\rbrack$ are called moments. As you might already have explored in the statistics related reference and have it that:
➀the mean, $\mu=E\lbrack X\rbrack$.
➁the variance, $\sigma^2=Var\lbrack X\rbrack=E\lbrack X^2\rbrack-E^2\lbrack X\rbrack$.
They are called the functions of moments, sometimes are difficult to found. The moment generating function provides an add-in in finding the k-th ordinary moment, the mean, and even more.
What is an MGF?
The MGF(moment generating function) of a random variable X, say it discrete, is usually given by:
$M_X(t)=E\lbrack e^{t\cdot X}\rbrack$
$\;\;\;\;\;\;\;\;=E\lbrack 1+\frac{t\cdot X}{1!}+\frac{(t\cdot X)^2}{2!}+\cdots+\frac{(t\cdot X)^k}{k!}+\cdots\rbrack$
Where $E\lbrack e^{t\cdot X}\rbrack$ exists in $\lbrack -h, h\rbrack$ for some $h$.
$E\lbrack X\rbrack$, called the first ordinary moment of random variable $X$. More precisely, denoted by $\mu_1$.
$E\lbrack X^2\rbrack$, also called the second ordinary moment of random variable $X$, denoted by $\mu_2$.
$E\lbrack X^k\rbrack$, also called the k-th ordinary moment of random variable $X$, denoted by $\mu_k$.
$e^{t\cdot X}=1$+$\frac{t\cdot X}{1!}$+$\frac{(t\cdot X)^2}{2!}$+$\cdots$+$\frac{(t\cdot X)^k}{k!}$+$\cdots$
By above Taylor series, the coefficient of $X^k$ is $\frac{t^k}{k!}$, hence, if $M_X(t)$ exists for $-h<t<h$, there must exist a mapping between the random variable $X$ and $e^{t\cdot X}$.
If $p(X)$ and $p(Y)$ has $M_X(t)=M_Y(t)$, that is to say $E\lbrack e^{t\cdot X}\rbrack$=$\lbrack e^{t\cdot Y}\rbrack$,then, the distribution of random variable $X$ and $Y$ are the same.
The Deduction Of The $\mu_k$
There exists a lof many peoperties of the MGF, but the majority of this article focus on the way to find out the k-th ordinary moment. Next to deduce the discrete MGF to express the moment.
➀
$M_X(t)=E\lbrack e^{t\cdot X}\rbrack$
$\;\;\;\;\;\;\;\;=E\lbrack\sum_{k=0}^\infty\frac{(t\cdot X)^k}{k!}\rbrack$
$\;\;\;\;\;\;\;\;=\sum_{k=0}^\infty\frac{E\lbrack X^k\rbrack\cdot t^k}{k!}$
where $E\lbrack X^k\rbrack$=$\mu_k$=$\sum_{i=1}^{\infty}(x_i)^k\cdot p(x_i)$, and $X={x_1,x_2,x_3,\cdots}$,
$\;\;\;\;\;\;\;\;=\sum_{k=0}^\infty\frac{\mu_k\cdot t^k}{k!}$
$\;\;\;\;\;\;\;\;=\sum_{k=0}^\infty\frac{\lbrack\sum_{i=1}^{\infty}(x_i)^k\cdot p(x_i)\rbrack\cdot t^k}{k!}$
$\;\;\;\;\;\;\;\;=\sum_{i=1}^\infty\sum_{k=0}^{\infty}\frac{(x_i)^k\cdot t^k}{k!}\cdot p(x_i)$
$\;\;\;\;\;\;\;\;=\sum_{i=1}^\infty e^{t\cdot x_i}\cdot p(x_i)$
➁
$E\lbrack e^{t\cdot X}\rbrack=\sum_{i=1}^\infty e^{t\cdot x_i}\cdot p(x_i)$
$\;\;\;\;\;\;\;\;=\sum_{i=1}^\infty(1$+$\frac{t\cdot x_i}{1!}$+$\frac{(t\cdot x_i)^2}{2!}$+$\cdots$+$\frac{(t\cdot x_i)^k}{k!}$+$\cdots)\cdot p(x_i)$
$\;\;\;\;\;\;\;\;=\sum_{i=1}^\infty 1\cdot p(x_i)$+$\sum_{i=1}^\infty\frac{t\cdot x_i}{1!}\cdot p(x_i)$+$\sum_{i=1}^\infty\frac{(t\cdot x_i)^2}{2!}\cdot p(x_i)$+$\cdots$+$\sum_{i=1}^\infty\frac{(t\cdot x_i)^k}{k!}\cdot p(x_i)$+$\cdots$
$\;\;\;\;\;\;\;\;=1$+$t\cdot\sum_{i=1}^\infty x_i\cdot p(x_i)$+$\frac{t^2}{2!}\cdot\sum_{i=1}^\infty (x_i)^2\cdot p(x_i)$+$\cdots$+$\frac{t^k}{k!}\cdot\sum_{i=1}^\infty (x_i)^k\cdot p(x_i)$+$\cdots$
$\;\;\;\;\;\;\;\;=1$+$t\cdot E\lbrack X\rbrack$+$\frac{t^2}{2!}\cdot E\lbrack X^2\rbrack$+$\cdots$+$\frac{t^k}{k!}\cdot E\lbrack X^k\rbrack$+$\cdots$
$\;\;\;\;\;\;\;\;=1$+$t\cdot \mu_1$+$\frac{t^2}{2!}\cdot \mu_2$+$\cdots$+$\frac{t^k}{k!}\cdot\mu_k$+$\cdots$
Therefore, all order of moment could be contained within MGF, which is the lemma.
➂we have the k-th derivatives of $M_X(t)$ with respect to $t^k$:
$\frac{\operatorname d^k M_X(t)}{\operatorname dt^k}$=$\mu_k$+$t\cdot \mu_{k+1}$+$\frac{t^2}{2!}\cdot \mu_{k+2}$+$\cdots$
, where $\frac{\operatorname d^k M_X(t)}{\operatorname dt^k}$=$\mu_k$, for $t=0$.
Therefore, we can say that for two random variables $X$, $Y$ having the same MGF, then, they have the same distributon.

 Gradually, it will approximate the normal distribution.
Gradually, it will approximate the normal distribution.
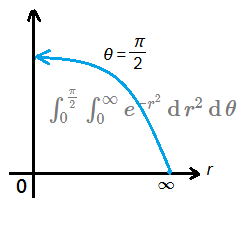 $I^2$=$\int_0^{\frac{\pi}{2}}\int_0^\infty e^{-r^{2}}\operatorname dr^2\operatorname d\theta$
$I^2$=$\int_0^{\frac{\pi}{2}}\int_0^\infty e^{-r^{2}}\operatorname dr^2\operatorname d\theta$ ➁the spread or dissemination of the distribution could be resort to $\beta$.
➁the spread or dissemination of the distribution could be resort to $\beta$. ➂$\lambda$ is for the intensity, that is, the rate, frequency, in the form of $\frac {count}{time unit}$.
➂$\lambda$ is for the intensity, that is, the rate, frequency, in the form of $\frac {count}{time unit}$.