29 Jun 2019
Prologue To Meshing The Rewards - Part 1
In order to avoid the local suboptimal endless looping, the suggestive approach is to mesh the reward funtion without impact on the original optimal policy. The reward function should contain not only the fixed return of constant, as we are losing benifit of value obtained in current state, when transiting from current state to next state.
Why To Change The Reward Function In MDP?
[1]
A brief summary
As we have a lot study in MDP, we know that state value chnages(or has been accumulated), which is enclosed with every occurrence of state transition:
➀it begins with initial configuration.
➁makes value iteration by Bellman equation(or operation), coming out some policy, maybe non-optimal, suboptimal, or even the final optimal.
➂then value improvement after policy iteration and leads to the very next policy improvement.
➃oever and over again, finally to the convergence.
[2]
Because of the state transition
We have learned the fact that the state value changes as transiting from current to next state. Should the reward function returns only the fixed constant values? We think it mandatory to reshape the reward function.
[3]
The common issue in AI
It would be easy to just turn the reward function into all zeros, then, all policies maximize that reward function, in which case, learning is done. But, this is not the problem we are trying to solve.
This is a common issue in AI.
[4]
The target
The reward function is a way to specify the behavior that is going to get compiled by the learning algorithminto actual behavior.
The semantics we’d like the agent to do by changing the reward function is for the efficiency:
➀speed of computation and experience that the agent needs to learn.
➁space of memory the learning algorithm requires.
➂solvability, infinity versus not-infinity.
We want to change the reward function without changing what it's originally optimizing.
Change The Reward Function
[Question]
How to change the reward function without changing the optimal policy?
[Answer]
We have defined MDP with states, actions, rewards, probability transition and gamma, denoted as $<S,A,R,P,\gamma>$.
By messing with $R$ only, and leaving all the rest uncganged:
➀multiply the reward function by any positive constant
➁shift the reward function by constant
➂non-linear potential-bsed rewards
Multiply $R$ By Positive Constant: Illustration
[Question]
$Q(S,A)$=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q(S’,A’)$
This is the Bellman equation we already familar with, and multiply $R(S,A)$ by constant $c$ to get the new reward function, that is $R’(S,A)$=$c\cdot R(S,A)$, where $c>0$, then what is $Q’(S,A)$=?
[Answer]
We are asking $Q’(S,A)$ in terms of $Q(S,A)$, let’s do the illustration:
$Q’(S,A)$
=$R’(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q’(S’,A’)$
=$c\cdot R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}($
$\;\;c\cdot R(S’,A’)$+$\gamma\cdot\sum_{S^{"}}P(S^{"}\vert S’,A’)\cdot max_{A^{"}}Q’(S^{"},A^{"}))$
where we have
$Q’(S’,A’)$
=$c\cdot R(S’,A’)$+$\gamma\cdot\sum_{S^{"}}P(S^{"}\vert S’,A’)\cdot max_{A^{"}}Q’(S^{"},A^{"}))$
in turn, we have
$Q’(S^{"},A^{"})$
=$c\cdot R(S^{"},A^{"})$+$\gamma\cdot\sum_{S^{'''}}P(S^{'''}\vert S^{"},A^{"})\cdot max_{A^{'''}}Q’(S^{'''},A^{'''}))$
still more, we have
$Q’(S^{'''},A^{'''})$
=$c\cdot R(S^{'''},A^{'''})$+$\gamma\cdot\sum_{S^{''''}}P(S^{''''}\vert S^{'''},A^{'''})\cdot max_{A^{''''}}Q’(S^{''''},A^{''''}))$
therefore,
$Q’(S’,A’)$
=$c\cdot R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}($
$\;\;c\cdot R(S’,A’)$+$\gamma\cdot\sum_{S^{"}}P(S^{"}\vert S’,A’)\cdot max_{A^{"}}Q’(S^{"},A^{"}))$
=$c\cdot (R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}($
$\;\;R(S’,A’)+\gamma\cdot\sum_{S^{"}}P(S^{"}\vert S’,A’)\cdot max_{A^{"}}(R(S^{"},A^{"})+…)))$
=$c\cdot Q(S,A)$
[Notes::1]
Multiply $R$ by zero leaves everything the same
If you multiply the reward function by zero, each state transition will bring zero as the return, all states’ value will all be zero, you will lose all the information.
[Notes::2]
$R$ negative multiply maximize the pain
If you multiply the reward function by negative value, then the convergence would end up in maximizing the pain, or by special design in policy iteration to converge in least pain.
Add Scalar To $R$: Illustration
[Question]
$Q(S,A)$=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q(S’,A’)$
This is the Bellman equation we already familar with, and add a scalar $c$ to $R(S,A)$ to get the new reward function, that is $R’(S,A)$=$R(S,A)+c$, then what is $Q’(S,A)$=?
[Answer]
We are asking $Q’(S,A)$ in terms of $Q(S,A)$, let’s do the illustration:
$Q’(S,A)$
=$R’(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q’(S’,A’)$
=$R(S,A)+c$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}($
$\;\;R(S’,A’)+c$+$\gamma\cdot\sum_{S^{"}}P(S^{"}\vert S’,A’)\cdot max_{A^{"}}Q’(S^{"},A^{"}))$
where we have
$Q’(S^{"},A^{"})$
=$R(S^{"},A^{"})+c$+$\gamma\cdot\sum_{S^{'''}}P(S^{'''}\vert S^{'''},A^{"})\cdot max_{A^{'''}}Q’(S^{'''},A^{'''}))$
therefore,
$Q’(S,A)$
=$R(S,A)+c$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}($
$\;\;R(S’,A’)+c$+
$\;\;\gamma\cdot\sum_{S^{"}}P(S^{"}\vert S’,A’)\cdot max_{A^{"}}(R(S^{"},A^{"})+c+…))$
=$Q(S,A)$+$c$+$\gamma\cdot c$+$\gamma^{2}\cdot c$++$\gamma^{3}\cdot c$+…
=$Q(S,A)$+$\frac {c}{1-\gamma}$
[Notes]
Adding scalar makes no impact on original policy
$Q(S,A)$+$\frac {c}{1-\gamma}$
=$R(S,A)$+$c$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}(Q(S’,A’)+\frac {c}{1-\gamma})$
proof:
$R(S,A)$+$c$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}(Q(S’,A’)+\frac {c}{1-\gamma})$
=$R(S,A)$+$c$
$\;\;$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q(S’,A’)$
$\;\;$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}\frac {c}{1-\gamma}$…➀
where the term ➀ could be further expanded:
$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}\frac {c}{1-\gamma}$
=$\gamma\cdot max_{A’}\frac {c}{1-\gamma}$
=$\gamma\cdot \frac {c}{1-\gamma}$
since $max_{A'}$ doesn't depend on this constant $\frac {c}{1-\gamma}$
therefore, we have
=$R(S,A)$+$c$
$\;\;$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q(S’,A’)$
$\;\;$+$\gamma\cdot \frac {c}{1-\gamma}$
in turn, $c$+$\gamma\cdot \frac {c}{1-\gamma}$=$\frac {1}{1-\gamma}$
finally,
=$R(S,A)$+$\frac {c}{1-\gamma}$
$\;\;$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q(S’,A’)$
=$Q(S,A)$+$\frac {c}{1-\gamma}$ is thus proved
Addendum
➀Meshing with rewards, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
29 May 2019
Prologue To Policy Iteration
Prior post reveals that value iteration eventually leads us to the optimal policy providing the action for the current state to take to get its maximum value when transiting to next state.
Departuring from multiple states in one MDP model, this article would guide you through value iteration to find the greedy policy in each state's transition, and finally get the optimal policy for each state. The whole process is called policy iteration.
Policy Iteration Versus Value Iteration
[1]
The beginning in MDP
Suppoose we are departuring from a beginning state in one MDP model, each time we do make a decision to choose the best action that can transit us to next state with the maximum value(or reward), and we are doing this over and over again, until we believe that we have build the optimal policy for each state, and it brings the whole MDP problem to a convergence.
This means that we are not facing the problem to choose the action of uncertainty in one single state, and the same state would then be re-visited, since we are repeating this over and over again.
There is no doubts that different or similar policies in one same state often interleave one over the others
, that’s the policy iteration process.
[2]
The concept of policy iteration
We have actually involved below 3 phases on the way to solve a MDP issue:
➀initially, $\forall S, Q_{0}(S)=0$…[A]
➁proceeds with policy improvement
$\forall S, \pi_{t}(S)$=$maxarg_{A}Q_{t}(S,A), t\geq 0$…[B]
➂do the policy evaluation task
$\forall S, Q_{t+1}(S)$=$Q^{\pi_{t}}(S)$…[C]
We are starting by picking any arbitrary $Q$ function, denote it the initialization step, that’s [A].
After that, we just iterate by taking the $t$-th, $Q_{t}$ function, computing its greedy policy, $\pi_{t}(S)$, that’s [B], then use that greedy policy to get a new $Q$ function, say $Q_{t+1}$, that’s [C].
And we are repeating and iterating this over and over again. So each time we go around in this loop, we rae taking our previous $Q$ function, finding its policy, taking that policy to find its next value function, such repeating would actually get convergence in finite time.
[3]
Policy iteration is a better way
The sequence of $Q$ functions we get convergence to $Q^{\ast}$ after we are experienced a series of value iteration in finite time, in particular, it illustrates how policy iteration works implicitely in my prior post.
The convergence of policy iteration is at least as fast as value iteration in that if at any point we sync up the $Q$ functions, we start value iteration and policy iteration from the same $Q$ function. Then, each step this policy iteration takes is moving us towards the optimal $Q$ function, no more slowly than value iteration.
So, policy iteration is a better way.
[4]
Concerns pertaining to policy iteration::mjtsai1974
One thing needs to be taken into consideration when we are doing the policy improvement task, that is faster convergence would be at the cost of greater computational expense.
In particular, when transiting from $S_{i}$ to $S_{i+1}$ in stage $t$, we’d like to make policy evaluation, $\forall S, Q_{t+1}(S)$=$Q^{\pi_{t}}(S)$, by taking the policy and working out $Q_{t+1}$ function to be used by $S_{i}$ as its value obtained, after transiting to $S_{i+1}$.
When in stage $t+1$, it does the policy improvement again, with the new updated(or even the same) policy come out, then $Q_{t+2}$ function would laterly be generated out, this cycle repeats, untile it converges.
Yes, it is solving a system of linaer equations.
The scenario might be constructed by putting value iteration inside the inner loop wrapper by the outside loop of policy iteration, since the value iteration operates in accordance to the policy, exactly, the action mapped from current state by current greedy policy at this moment. So, the value iteration should be in the inner loop of policy iteration.
Trivially, the policy iteration is doing much works than value iteration, if the greedy policy seldomly changes on its way to convergence, it should be at least as fast as value iteration.
Why Does Policy Iteration Works?
[1]
What is the convergence time?
➀we know there exists some MDPs, the number of iterations the policy iteration takes is linear, it is at lease as large as the number of states in the MDP.
➁the worse case is that it can't be larger than the number of actions raised to the number of states.
$\;\;l$inear $\vert S\vert\leq$ convergence time $\leq \vert A\vert^{\vert S \vert}$
[2]
Domination
➀the domination:
$\pi_{1}\geq\pi_{2}$ iff $\forall s\in S, V^{\pi_{1}}(s)\geq V^{\pi_{2}}(s)$
➁the strict domination:
$\pi_{1}>\pi_{2}$ iff $\forall s\in S, V^{\pi_{1}}(s)\geq V^{\pi_{2}}(s)$
there exists some $s\in S, V^{\pi_{1}}(s)> V^{\pi_{2}}(s)$
➂$\pi$ is $\varepsilon$ optimal iff $\vert V^{\pi}(s)-V^{\pi^{\ast}}(s)\vert\leq\varepsilon$
Expand further that a policy is $\varepsilon$ optimal if the value function for that (greedy) policy is $\varepsilon$ close to the value function for the optimal policy at all states. It gives us a concept of bounding loss or bounding regret.
We can treat a policy to be nearly optimal if per step loss in each state transition is very very small.
From above we can tell that if policy 1 dominates policy 2, but, not strictly dominates it, then they must have the same value everywhere. Since it would never be greater than or equal to, it’s always equal to.
[3]
Bellman operator is monotonic
We define 2 Bellman operator on 2 policies, they are $B_{1}$, $B_{2}$ on $\pi_{1}$, $\pi_{2}$:
➀$\lbrack B_{1}V\rbrack$=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,\pi_{1})\cdot V(S’)$
➁$\lbrack B_{2}V\rbrack$=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,\pi_{2})\cdot V(S’)$
So, if we use $B_{1}$ over value function, it just returns the immediate reward, plus the discounted expected value following $\pi_{1}$, the same idea for $B_{2}$, and it is using $\pi_{2}$.
We already know a bunch of things about such updates. If we apply the same Bellman operator on distinct value functions, then they are not moving further apart, by a factor of at least gamma, unless these 2 value functions are the same.
If ther are already perfectly together, staying at the same fixed point, then they won't move any close together.
[4]
Policy iteration behaves itself
$\;\;$ if $V_{1}\geq V_{2}$, then $B_{2}V_{1}\geq B_{2}V_{2}$.
proof::mjtsai1974
$\lbrack B_{2}V_{1}-B_{2}V_{2}\rbrack(S)$
=$\gamma\cdot\sum_{S’}P(S’\vert S, \pi_{2})\cdot (V_{1}(S’)-V_{2}(S’))$
, where the term $(V_{1}(S’)-V_{2}(S’))\geq 0$ by given.
Then, we take a convex combination of a bunch of non-negative values by summing them up, there is no way it would be negative.
We thus proved that $V_{1}$ dominates $V_{2}$ leads to $B_{2}V_{1}$ dominates $B_{2}V_{2}$.
[5]
Cautions::mjtsai1974
The same Bellman operator with the same greedy policy, might not guarantee $S_{1}$ and $S_{2}$ could get closer after this transition.
Because the same policy working on different states might not come out with the same action, even the same action might leads to different one step transition.
In above proof, we are applying on the same state, but different value functions.
Value Improvement In Policy Iteration
[1]
The background
Suppose in the beginning, we are given Bellman operator $B_{1}$ applied on some policy $\pi_{1}$ with respect to value function $Q_{1}$, such that $Q_{1}$=$B_{1}Q_{1}$ holds.
Still more, there exists another Bellman operator $B_{2}$ applied on a greedy policy $\pi_{2}$ with respect to value function $Q_{1}$, such that $Q_{1}\leq B_{1}Q_{1}$ holds.
Above construction holds by contraction property. We have this inequality:
$Q_{1}(S,A)$
=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S, \pi_{1}(S’))\cdot Q_{1}(S’,\pi_{1}(S’))$
$\;\;\leq R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S, \pi_{2}(S’))\cdot Q_{1}(S’,\pi_{2}(S’))$
Image we are beginning from state $S$ by using $B_{1}$ on $\pi_{1}$ to reach $Q_{1}$, as it is the fixed point of $B_{1}$, that is to say you start off with the policy, and you get the value function of that policy.
Then, we might back to the same state $S$, since we are repeating the value iteration over and over again, thus back to the original departuring point, under the case we are in the MDP model already known; or we are just evaluating over the sampling data, trying to complete the contour of this MDP model, eventhough, we still have the chance to re-visit the state we have ever arrived, say the initial state $S$.
This time, intuitively, we take $B_{2}$ following up $\pi_{2}$, this greedy policy would turn our value function $Q_{1}$ no worse, possibly better, that is $Q_{1}\leq B_{2}Q_{1}$.
[2]
The policy iteration moves in the right direction
We have put all the things together to prove policy iteration moves in the right direction:
➀the Bellman operator monotonicity
➁the value improvement property
➂the definition of $\pi_{1}$,$\pi_{2}$,$B_{1}$,$B_{2}$,$Q_{1}$,$Q_{2}$
[3]
The policy iteration in a summary
➀$B_{2}Q_{1}\geq Q_{1}$…value improvement
➁$k\geq 0, B_{2}^{k+1}Q_{1}\geq B_{2}^{k}Q_{1}$…monotonicity
➂$lim_{k\rightarrow\infty}B_{2}^{k}Q_{1}\geq Q_{1}$…transitinity
➃$Q_{2}\geq Q_{1}$…fixed point
Policy Iteration Won't Get Stuck In Local Optimal
[1]
The important thing
If there is any way to impriove, it will actually improve, it won't get stuck in local optimal. This is really the very important thing.
[2]
Value non deprovement or value improvement
If it’s the case that $\pi_{1}$ is optimal, then the greedy policy $\pi_{2}$ would just lead the value function to the the same fixed point. We are just stuck at the same fixed point. Because we have already reached the fixed point, that’s the whole thing.
If it’s the case that $\pi_{1}$ is not optimal, there has some space that makes value non deprovement equivalent to value improvement and it holds for this inequality:
$Q_{1}(S,A)$
=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S, \pi_{1}(S’))\cdot Q_{1}(S’,\pi_{1}(S’))$
$\;\;\leq R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S, \pi_{2}(S’))\cdot Q_{1}(S’,\pi_{2}(S’))$
The important thing is that it might like strict value improvement for some states, replacing $\geq$ by $>$.
Illustration: More On Value Non-deprovement And Value Improvement
[Question]
Suppose I have 2 states, and keep on swapping back and forth in between $S_{1}$ and $S_{2}$ per iteration, to evaluate which one is betterthan the other. The question is that after swapping, do you still have domination in both cases? The MDP model is exhibitted below:
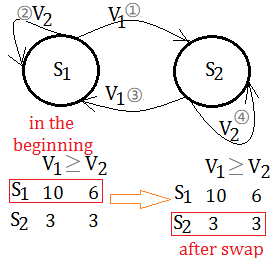Trivially, in $S_{1}$, $V_{1}$ is more value than $S_{1}$, $V_{2}$.
[Answer]
No, because domination is point wise, state wise.
If you don’t consider value non-deprovement, you can swap in between $S_{1}$ and $S_{2}$. Suppose you are looping over and over again in this MDP, time to converge, at this moment in $S_{1}$, with $V_{1}> V_{2}$, after you transite to $S_{2}$, you have value functions $V_{1}\geq V_{2}$, which is a violation. Value non-deprovement and value Improvement don't allow value function go down, it should at least keep the same!!!
The point is that the statement is for all the states, for their value functions, once $V_{1}$ is strictly dominating $V_{2}$ in $S_{1}$, after transiting to $S_{2}$, should keep it that way.
So, local stuck doesn't happen if we are already in the unique fixed point with strict domination, in this example $S_{1}$; however, if we are beginning from $S_{2}$, if should transite to $S_{1}$ for no worse, even better.
[Notes::mjtsai1974]
By policy iteration, we'll always get a better policy.
Since if we are starting from $S_{1}$ by $\pi_{1}$, the initial policy of something, by picking up $A_{1}$ to transite to $S_{2}$. We are at least one step toward the final optimal in $S_{2}$ at this moment, or it is not worse, might be the same, even better than it is in $S_{1}$.
Addendum
➀Advanced, algorithmic, analysis, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
10 May 2019
Prologue To Linear Programming In Value Iteration
Prior post reveals that value iteration doesn't give us a polynomial time algorithm for solving MDPs. The linear programming is the current only way to solve MDPs in polynomial time.
$\frac {1}{1-\gamma}$ Isn't Polynomial $\approx$ Isn't Proportional
The value iteration identifies an optimal policy and polinomial time in $\frac {1}{1-\gamma}$, where $\lim_{\gamma\rightarrow 1}\frac {1}{1-\gamma}$=$\infty$, just explodes. That’s why we need the linear programming to solve MDPs in a reasonable amount of time.
What’s Linear Programming?
[1]
Encode MDP solution as a linear program
In my prior post Lagrange Multiplier, you can find some similarity. In this post, we’d like to dive into deep level to solve MDPs by means of linear programming:
➀it’s an optimization framework, in which you can give linear constraint in a linear objective function.
➁as long as the number of variables and costraints are polynomial, we can get a solution in polynomial time.
➂we need to encode MDP solution as a linear program, we thus can have linear constraint(s) and a linear objective function.
[2]
How to solve a MDP?
For the time being, in this series of RL posts, we just need to solve the Bellman equation:
$\forall S, V(S)$=$max_{A}(R(S,A)+\gamma\sum_{S’}P(S’\vert S,A)\cdot V(S’))$…[A]
➀for each state $S$, we have a variable $V(S)$ and relate each distinct $V(S)$ to its next $V(S’)$.
➁we thus have ➀ to be a set of constraints. If we could solve this set of constraints, it is suggested to be a good departure point.
[3]
Do we have a way to solve [A]?
Unlessthe $max_{A}$ has become linear, the answer is no.
The max over action is not linear, it isn't translatable directly to a set of linear equations and a linear objective function. In the very beginning, we are given a set of non-linear equations.
We should express the max over action in terms of a set of linear constraints and a linear objective function.
[4]
Example of $max(-3,7,2,5)=X$
Given this example of max, below is a set of inequality constraints:
➀$X\geq -3$
➁$X\geq 7$
➂$X\geq 2$
➃$X\geq 5$
Here we ponder if the solution $7$ to this set of inequality constraints is exactly the max? The answer is no, and why? Because $9$, $10$, these numbers are also greater than or equal to all of these things(the set of constraints).
What we want is to pick up the smallest one within those number greater than and equal to above set of inequalities, in this example, you can’t get any number that is smaller than $7$, thta is $min X$=$7$.
Is $min X$ a linear operator? No, it is just a linear objective function!!! Next, we are going to use this idea to generalize a linear objective function of the Bellman equation in a very similar way.
The Linear Programming: Primal
[1]
Refine the Bellman equation
Succeeding to above idea that we’d like to pick up the smallest one from within all possible value functions of maximum, we should refine our Bellman equation in [A] as below:
$\forall S,A\;V(S)\geq R(S,A)+\gamma\sum_{S’}P(S’\vert S,A)\cdot V(S’)$…[B]
➀for all states and actions, the value of a state is greater than or equal to the right part of the original expression, and we say the new expression of inequality [B].
➁the whole right part of [B] is just the Q-value.
[2]
What and how do we minimize here?
Caution must be made that we are given a set of sampling data of a MDP model:
➀since inequality [B] is refined for all states and actions, what we want to minimize is not a single state.
➁inequality [B] aims at all states, what we should minimize is a vector.
➂a single $V(S)$ is unbounded, we should as a whole evaluate all states in one minimize operation.
Due to above concerns in ➀,➁,➂, it turns out to minimize the sum of all states to make it work:
$min\;\sum_{S}V(S)$…[C]
So, $min\;\sum_{S}V(S)$ is going to operate on all the individual $V(S)$ and make each of them to be as small as they can be, so that it actually equals the $max\;V(S)$ for all $S$.
Besides, $min\;\sum_{S}V(S)$ isn't an upper bound on the max, if any distinct $V(S)$ is an upper bound, then you won't have the minimum sum. You can always move it down a little bit.
[3]
The primal
This is atually a linear program by putting [B] and [C] together, some textbook name it the primal:
$\;\;\forall S,A\;V(S)\geq R(S,A)+\gamma\sum_{S’}P(S’\vert S,A)\cdot V(S’)$
$\;\;\;\;min\;\sum_{S}V(S)$
You can regard [C] as the linear objective function. To be believed that it is the solution equivalent to the solution to the MDP. We can just write down this linear program and give it to a linear program solver that runs in polynomial time and finally gets $V(S)$ for all state $S$.
How do we get our policy from that? We just choose the action that always returns the best(maximum) value, choose this greedy policy with respect to that optimal value function, and we are doing it in the unit of each distinct state.
Linear Programming Duality
[1]
A mechanical process
One more thing about linear programming is by switching from the primal to what’s called the dual. It has such nice property that by:
➀changing constraints into variables
➁changing variables into constraints
You can get a new linear programming that is equivalent to the original old one, this is called the linear programming duality. Sometimes, it would be useful to solve a MDP by putting bounds and constraints on the solutions.
We treat the process of producing the dual of linear programming to be just a mechanical process.
[2]
The dual
$max_{q_{S,A}}\sum_{S}\sum_{A}q_{S,A}\cdot R(S,A)$…[D]
$\;\;$such that $1$+$\gamma\cdot\sum_{S}\sum_{A}q_{S,A}\cdot P(S’\vert S,A)$=$\sum_{A’}q_{S’,A’}$…[E]
$\;\;\;\forall S,A\;q_{S,A}\geq 0$…[F]
➀[D] is the linear objective function.
➁[E] and [F] are the constraints.
We perform a series of steps to turn each constraint from the primal becomes variable in the dual, each variable in the primal becomes constraint in the dual, and maximum becomes minimum, bound becomes objective function.
In more detail, the $V(S)$ and $R(S,A)$ term in [B], the constraint of primal, has been turned into the variables in the linear objective function expressed by [D] in dual, with $V(S)$ be replaced with $q_{S,A}$, which is the next new introduced concept, the aganet flow.
[3]
New introduced policy flow
In this dual, the optimization is to maximize the sum over all state-action pairs of the reward for that state-action pair times the value of $q_{S,A}$, which is the new introduced policy flow; it’s not the same Q-value.
The policy flow, $q_{S,A}$ could be regarded as how much agentness is flowing through each state-action pair. If it follows the policy, it is going to spend some time running in that environment of MDP, passing through each state-action pair. When it is transiting from current state-action pair to its next state-action pair, it is discounted by $\gamma$.
Here is the concept that each time the policy flow passes through a state-action pair, we’re going to get the reward associated with that state-action pair. What we’d like to do is to maximize the reward according to this concept by means of $max_{q_{S,A}}\sum_{S}\sum_{A}q_{S,A}\cdot R(S,A)$.
[4]
Min in primal vs max in dual
It’s more intuitive for we do the maximizing job in the dual, comparing with the minimum we do in the primal. What we don't want is to have an upper bound in the primal, that’s why we choose to minimize the sum of all states’ value.
We choose $max_{q_{S,A}}\sum_{S}\sum_{A}q_{S,A}\cdot R(S,A)$, [D] in the dual to maximize our reward each time the agent flow passing through each state-action pair, how to guarantee that we won't have an upper bound of each or some state-action pair? This is a good question.
It’s going to be subject to the following idea, or just the constraint.
[5]
$1$+$\gamma\cdot\sum_{S}\sum_{A}q_{S,A}\cdot P(S'\vert S,A)$=$\sum_{A'}q_{S',A'}, \forall A'$
The answer is that we are constrainting this maximum to [D], that’s a constraint, and for each state, in this case, would be better if we think oif them as next state.
For each possible next state $S'$, our design expects it to be true that the amount of policy flow through that next state $S'$, summed up over the actions $A'$ that are going out through it, should be equal to the number of times that the next state $S'$ is visited, which we can get by summing over all states(represented by $S$) we might have started out, and actions $A$ we might have taken from $S$.
➀the policy flow through that state-action pair times the transition probability that would send us from $S$ to $S’$ by action $A$.
➁we include $1$ in it, because we can also start any given state-action pair.
So, there is some policy flow we’re injecting into each state-action pair of the system. And we are going to add to this same state-action pair any other policy flow that would be coming through it, after that, in turns through other parts of the system.
[6]
It is discounted by $\gamma$
It’s like we are dumping policy flow over MDP, then let the MDP pump around what’s left.
It is discounted by $\gamma$. We ultimately get the maximum possible reward by $max_{q_{S,A}}\sum_{S}\sum_{A}q_{S,A}\cdot R(S,A)$, if we just follow the greedy policy at each state we have visited.
[7]
The additional constraint: $\forall S,A\;q_{S,A}\geq 0$
This additional constraint just to guarantee 2 things:
➀there is no negative policy flow.
➁the policy flow in one place wouldn't be overestimated, so that it wouldn't then be drained out in some other place to blance it.
It is a meaning flow of balance, so the amount of stuff going into $S'$ has to be equal to the amount of stuff coming out of it.
Subject to this constraint of $1$+$\gamma\cdot\sum_{S}\sum_{A}q_{S,A}\cdot P(S’\vert S,A)$=$\sum_{A’}q_{S’,A’}, \forall A’$, would we maximize the reward by $max_{q_{S,A}}\sum_{S}\sum_{A}q_{S,A}\cdot R(S,A)$.
Addendum
➀Advanced, algorithmic, analysis, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
21 Apr 2019
Prologue To More On Value Iteration
Prior post details the way contraction mapping makes value iteration converges. This post would dive a little bit on the horizontal length for convergence.
$\frac {1}{1-\gamma}$ Bits Of Precision
We’d like to dive a little bit to relate the horizontal length to the convergence, by below given:
➀denote the dimensionality of states and actions as $\vert S\vert$ and $\vert A \vert$.
➁also with $R_{max}$=$max_{S,A}\vert R(S,A)\vert$.
➂$\frac {1}{1-\gamma}$ as bits of precision.
➃for some $t^{\ast}$ polynomial in $\vert S\vert$ and $vert A \vert$.
[1]
There is some time before infinity
➀$\pi(S)$=$argmax_{A}Q_{t^{\ast}}(S,A)$ is optimal.
➁we treat the $Q^{\ast}$ to be the $Q$ function after we iterate over $t^{\ast}$ times, we know that it converges in the limit, $Q_{t}$ eventually goes to $Q^{\ast}$.
$\Rightarrow$Here is the hint that we found there is some $t^{\ast}$ of finite horizon, less than infinity, that’s polynomial in:
➀the number of states
➁the number of actions
➂the magnitude of the rewards in the reward function
➃the number of bits of precision that are used to specified the transition probability
➄number of bits of $\gamma$ in $\frac {1}{1-\gamma}$
$\Rightarrow$So, that, if we run value iteration for that many steps, the $Q$ function that we get out is $Q_{t^{\ast}}$ of $(S,A)$. If we define a policy $\pi(S,A)$, which is just the greedy policy with respect to that $Q$ function, then that policy is optimal.
$\Rightarrow$We know that in the limit, if we run value iteration for an infinite number of steps, then the $Q$ function that we get at that point, the greedy policy with respect to the $Q$ function, is just optimal.
$\Rightarrow$This leads to a finding that there is sometime before infinity where we get a $Q$ function that's close enough, so that if you do the greedy policy with respect to it(the $Q$ function), it really is optimal. Like all the way $100\%$ optimal.
$\Rightarrow$What that really means is that it's polynomial(all the way $100\%$ optimal) and you can actually solve this in a reasonable amount of time.
[2]
$\frac {1}{1-\gamma}$ is not so just polynomial
The whole convergence might not be so just polynomial, why? The $\gamma$ in $\frac {1}{1-\gamma}$ is the key factor, as $\gamma\rightarrow 1$, this blows up and that's not polynomial bounded, say the number of bits it takes to write down $\gamma$.
$\Rightarrow$So, it’s exponential in terms of the number of bits it takes to write down the whole problem.
$\Rightarrow$But even so, if you take $\gamma$ to be some fixed constant, the $\frac {1}{1-\gamma}$ might be really big, but, it’s some fixed constant and we are polynomial in all the rest of $\vert S\vert$,$\vert A\vert$, $R_{max}=max_{S,A}R(S,A)$.
$\Rightarrow$This leads to an idea that once you fix an MDP model and the number of bits of precision $\gamma$, there is going to be some optimal action and there might be other actions that are tied for optimal in any given state.
$\Rightarrow$One thing to be noted about the second best action is going to be some bounded amount away from optimal. It can't get any arbitrary close to optimal. It’s going to be some distance away. This says when we run value iteration enough, eventually, the final distance between the best action and the second best action gets bigger than this original gap.
➀once it’s bigger than this gap, then the greedy policy is going to be functioning work as optimal policy.
➁it's going to start to choose the best action by optimal policy in all states, maybe at this moment.
$\Rightarrow$The greedy policy with respect to value iteration converges in a reasonable amount of time.
The Largest Difference Between Optimal Policy And Greedy Policy: $max_{S}\vert V^{\pi_{V_{t}}}(S)-V^{\ast}(S)\vert$<$\frac {2\cdot\varepsilon\cdot\gamma}{1-\gamma}$
[1]
The background
if $\vert V_{t}(S)-V_{t+1}(S)\vert<\varepsilon$,
$\;\;\forall S$, then, $max_{S}\vert V^{\pi_{V_{t}}}(S)-V^{\ast}(S)\vert$<$\frac {2\cdot\varepsilon\cdot\gamma}{1-\gamma}$
Here is the assumption that
➀we run value iteration and get a series of value functions, say $V_{t}$.
➁the amount of changes of $V_{t}$, from $t$ to $t+1$, is less than $\varepsilon$ for all states $S$ in this MDP model.
Then, the largest difference between the optimal value function $V^{\ast}(S)$ and the value function we get by taking the greedy policy with respect to the value function at time $t$ is small, say $\frac {2\cdot\varepsilon\cdot\gamma}{1-\gamma}$.
[2]
Why end up being $\frac {2\cdot\varepsilon\cdot\gamma}{1-\gamma}$?
➀because this($\frac {1}{1-\gamma}$) little bit of $\varepsilon$ that we could be off, could be magnified, even every single step as we think about this into future. That’s why we get a $1-\gamma$ in the denominator.
➁there exists $2$ sides of $\varepsilon$, positive and negative for each, that’s why we have $2$ times $\varepsilon$.
➂suppose we are at $t$, such change doesn't take place right now at $t$, it takes one step further into $t+1$, then we need to times $\gamma$.
If you have a good enough approximation of the value function, then you can at least put a bound on ➀how far off you are in terms of following the resulting greedy policy value function $V^{\pi_{V_{t}}}(S)$ from ➁how far that is following the optimal policy value function $V^{\ast}(S)$.
[3]
Should we need to know how closed we are to $V^{\ast}$?
We don't even need to know how closed we are to $V^{\ast}$, all we need is $\vert V_{t}(S)-V_{t+1}(S)\vert$<$\varepsilon$ for all $S$, that is any two consecutive iteration of value iteration:
➀that just gives us a bound on what if we stops now and follow that policy $\pi_{V_{t}}$.
➁knowning that value iteration eventually converges in the limit of $\varepsilon$ is not so helpful, because you don't know when the converges takes place.
➂$max_{S}\vert V^{\pi_{V_{t}}}(S)-V^{\ast}(S)\vert$<$\frac {2\cdot\varepsilon\cdot\gamma}{1-\gamma}$ is telling us when is the decent time(right moment) to stop.
[4]
Pick up smaller $\gamma$
If $\gamma$ is tiny, then, $\frac {1}{1-\gamma}$ stays small, $\frac {2\cdot\varepsilon\cdot\gamma}{1-\gamma}$ also stays small. It’s all good.
➀the more closer $\gamma$ gets to $1$, the more problematic your learning convergence would be.
➁$\gamma$ tells you what your horizon is.
➂the smaller $\gamma$ puts small weight on the relation of next state to the current state, then the state convergence would not over too long a horizon.
➃as $\gamma$ gets closer to $1$, $\frac {1}{1-\gamma}$ would just explodes, it takes you to look ahead a lot further, it’s a harder problem, since it is over a longer horizon.
The smaller and larger $\gamma$ leads to a trade off between the horizon and the feasibility of solving a problem in a rreasonable amount of time.
$\vert\vert B^{k}Q_{1}-B^{k}Q_{2}\vert\vert_{\infty}\leq\gamma^{k}\vert\vert Q_{1}-Q_{2}\vert\vert_{\infty}$
if you start from with $Q_{1}$ and we run $k$ steps of value iteration, in other words, we apply the Bellman operator $k$ times, that is to say the $k$ step Bellman operator is a contraction mapping.
The index of contraction is just like $\gamma$ raised to the $k$, which is a much much smaller number.
So running $k$ steps of value iterations actually makes your value functions much closer together than one single step value iteration.
Cautions must be made that $\gamma$ raised to the $k$ is not linear, it’s like gamma squared, gamma cubed, gamma to the $k$, that’s the index of contraction. So, if we run $10$ steps of value iteration, that’s like running $1$ step in $10$ steps of value iteration, because the difference $<\frac {2\cdot\varepsilon\cdot\gamma}{1-\gamma}$ always holds.
$\vert\vert B^{k}Q_{1}-B^{k}Q_{2}\vert\vert_{\infty}\leq\gamma^{k}\vert\vert Q_{1}-Q_{2}\vert\vert_{\infty}$
gives us a way of quantifying how long we run value iteration and connecting it with how close you are to optimal after you run $k$ steps of value iteration.
Addendum
➀Advanced, algorithmic, analysis, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
17 Mar 2019
Prologue To The Bellman Operator And Convergence Properties
The Bellman operator of contraction mapping makes the statement of convergence concrete and come out the major properties.
The Statement of Convergence
[1]
The statement
➀let B be an operator of contraction mapping, and $Q^{\ast}$=$BQ^{\ast}$ be it’s fixed point.
➁let $Q_{0}$ be a $Q$ function, and define $Q_{t+1}$=$\lbrack B_{t}Q_{t}\rbrack Q_{t}$, then $Q_{t}\rightarrow Q^{\ast}$.
Suppose we have been given some sequence of $Q$ functions.
➀it starts off with $Q_{0}$ and the way we’re going to generate the next step from the previous step, is that we are going to have a new kind of operator, $B_{t}$.
➁$B_{t}$ is going to be applied to $Q_{t}$, producing an operator $\lbrack B_{t}Q_{t}\rbrack$ that we then apply to $Q_{t}$, and that’s what we assign $Q_{t+1}$ to be.
So, in the context of $Q$ learning, this is essential the $Q$ learning update, there exists 2 different $Q$ functions that are used in the $Q$ learning update:
➀one is the $Q_{t}$ function in $\lbrack B_{t}Q_{t}\rbrack$ that is used to average together, to take care of the fact there is noise in the probabilistic transitions of stochasticity.
➁the other one is the $Q_{t}$ that we are using in the one step look ahead as part of the Bellman operation.
[2]
Notes::mjtsai1974
➀we can treat the term $\lbrack B_{t}Q_{t}\rbrack$=$B_{t++}$, be noted that it is $t$ plus plus, not $t+1$.
➁$t$ plus plus means that we starts from $t$, with some effort of plus plus to gain some reward maybe. If we are from $t+1$, then we say $\lbrack B_{t+1}Q_{t+1}\rbrack$=$B_{(t+1)++}$.
➂in the final fixed point of $Q^{\ast}$=$BQ^{\ast}$, the $B$ term is actually $B_{\ast}$.
The Convergence Property 1
The cool thing is that this sequence of $Q$ functions, starting from any $Q_{0}$, by keeping applying $Q_{t+1}$=$\lbrack B_{t}Q_{t}\rbrack Q_{t}$, we’re going to approach $Q^{\ast}$, as long as we have certain properties holding on how we define this $B_{t}$.
For all $U_{1}$,$U_{2}$, $S$, $A$:
$\;\;\vert(\lbrack B_{t}U_{1}\rbrack Q^{\ast})(S,A)-(\lbrack B_{t}U_{2}\rbrack Q^{\ast})(S,A)\vert$
$\;\;\leq(1-\alpha_{t}(S,A))\cdot\vert U_{1}(S,A)-U_{2}(S,A)\vert$
, where the littlecase $t$ says that $B$ is applied onto the $t$-th state’s current transition to next $t+1$ state.
proof::mjtsai1974
$\Rightarrow$Recall that in Bellman Operator Makes Convergence:
$\;\;\lbrack BQ\rbrack(S,A)$=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q(S’,A’)$
➀if we take $Q^{\ast}$=$BQ^{\ast}$, this indicates that
$Q^{\ast}(S,A)$=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q_{any}(S’,A’)$
, we can transite from any $Q$, the $Q_{any}$ to $Q^{\ast}$
, where $Q_{any}$=$\{Q_{t},Q_{t+1},Q_{t+2},…Q^{\ast}\}$
➁therefore, we have it holds:
$Q_{t+1}(S,A)$=$R(S,A)$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q_{t}(S’,A’)$
$\Rightarrow\lbrack BQ\rbrack$ is a kind of operator, could be used to apply on $Q$. By $TD(0)$, we can establish it:
$(\lbrack BQ_{T-1}\rbrack Q_{T-1})(S,A)$
=$Q_{T}(S,A)$
=$Q_{T-1}(S,A)$+$\alpha_{T}\cdot(R(S,A)$
$\;\;$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q_{T-1}(S’,A’)-Q_{T-1}(S,A))$
, where uppercase $T$ stands for the $T$-th eposide from state $S$ to state $S'$.
$\Rightarrow$Take $(\lbrack BQ_{T-1}\rbrack Q_{T-1})(S,A)$’s first $Q_{T-1}$ term as $U_{1}$ and $U_{2}$, and have the second $Q_{T-1}$ term replaced by $Q^{\ast}$, then:
$\vert(\lbrack BU_{1}\rbrack Q^{\ast})(S,A)-(\lbrack BU_{2}\rbrack Q^{\ast})(S,A)\vert$
=$\vert\alpha_{U_{1}}\cdot(R(S,A)$
$\;\;$+$\gamma\cdot\sum_{S’}P_{U_{1}}(S’\vert S,A)\cdot max_{A’}Q^{\ast}(S’,A’)-Q^{\ast}(S,A))$
-$\alpha_{U_{2}}\cdot(R(S,A)$
$\;\;$+$\gamma\cdot\sum_{S’}P_{U_{2}}(S’\vert S,A)\cdot max_{A’}Q^{\ast}(S’,A’)-Q^{\ast}(S,A))\vert$
=$\vert\alpha_{U_{1}}\cdot D_{U_{1}}-\alpha_{U_{2}}\cdot D_{U_{2}}\vert$
, where the update term $D_{U_{i}}$, could be expressed as:
$R(S,A)$+$\gamma\cdot\sum_{S’}P_{U_{i}}(S’\vert S,A)\cdot max_{A’}Q^{\ast}(S’,A’)$-$Q^{\ast}(S,A))$
, and $i$=$1,2$ in this proof.
$\Rightarrow$Continue above deduction:
$\vert\alpha_{U_{1}}\cdot D_{U_{1}}-\alpha_{U_{2}}\cdot D_{U_{2}}\vert$
$\approx\vert(D_{U_{1}}-\frac {\alpha_{U_{2}}}{\alpha_{U_{1}}}\cdot D_{U_{2}})\vert\cdot\alpha_{U_{1}}$
$\leq\vert(1-\frac {\alpha_{U_{2}}}{\alpha_{U_{1}}})\cdot (D_{U_{1}}-D_{U_{2}})\vert\cdot\alpha_{U_{1}}$…[A]
$\Rightarrow$Why it holds?
Because $(D_{U_{1}}-\frac {\alpha_{U_{2}}}{\alpha_{U_{1}}}\cdot D_{U_{2}})\leq(1-\frac {\alpha_{U_{2}}}{\alpha_{U_{1}}})\cdot (D_{U_{1}}-D_{U_{2}})$…[B]
$\Leftrightarrow$
$maxarg(D_{U_{1}})$=$1$
$maxarg(D_{U_{2}})$=$\frac {\alpha_{U_{2}}}{\alpha_{U_{1}}}$
$maxarg(D_{U_{1}}-D_{U_{2}})$=$1-\frac {\alpha_{U_{2}}}{\alpha_{U_{1}}}$
, it is the maximum non-expansion.
$\Rightarrow$Multiplying both side of [B] with $\alpha_{U_{1}}$ would we get [A], then:
➀take $1-\alpha_{T}$=$(1-\frac {\alpha_{U_{2}}}{\alpha_{U_{1}}})\cdot\alpha_{U_{1}}$, we just get the inequality proved.
➁take $T$=$t$, for we are evaluating the $t$-th transition by $T$-th eposide, then we get
$(1-\alpha_{t})\cdot (D_{U_{1}}-D_{U_{2}})$…[C]
➂next, add the term $Q_{T-1}(S,A)$
$(1-\alpha_{t})\cdot (Q_{T-1}(S,A)+D_{U_{1}}-(Q_{T-1}(S,A)+D_{U_{2}}))$…[D]
, which is identical to [C].
$\Rightarrow$Finally, we establish this property:
$\;\;\vert(\lbrack B_{t}U_{1}\rbrack Q^{\ast})(S,A)-(\lbrack B_{t}U_{2}\rbrack Q^{\ast})(S,A)\vert$
$\;\;\leq(1-\alpha_{t}(S,A))\cdot\vert U_{1}(S,A)-U_{2}(S,A)\vert$
, in this proof we’re expressing the distinct $U_{1}$ and $U_{2}$ in terms of temporal difference form:
$Q_{T}(S,A)$
=$Q_{T-1}(S,A)$+$\alpha_{T}\cdot(R(S,A)$
$\;\;$+$\gamma\cdot\sum_{S’}P(S’\vert S,A)\cdot max_{A’}Q_{T-1}(S’,A’)-Q_{T-1}(S,A))$
➀$T$ means the $U_{1}$, $U_{2}$ is evaluating in the $T$-th eposide for their state transition.
➁take $T$=$\{T_{U_{1}}, T_{U_{2}}\}$, if $T_{U_{1}}$=$T_{U_{2}}$, the proof just makes it right; however, the difference won't become larger even if $T_{U_{1}}\neq T_{U_{2}}$, and we keep on applying this Bellman operator oevr and oevr again!!!
This proof says we do the Bellman update on $U_{1}$ and $U_{2}$, finally learned the $Q^{\ast}(S,A)$-value.
The Convergence Property 2
For all $Q$,$U$,$S$,$A$:
$\;\;\vert(\lbrack B_{t}U\rbrack Q^{\ast})(S,A)-(\lbrack B_{t}U\rbrack Q)(S,A)\vert$
$\;\;\leq(\gamma\cdot\alpha_{t}(S,A))\cdot\vert Q^{\ast}(S,A)-Q(S,A)\vert$
, if we hold $U$ fixed, then we get the contraction of $Q$ toward $Q^{\ast}$, by applying $\lbrack B_{t}U\rbrack$ onto $Q^{\ast}$ and $Q$.
proof::mjtsai1974
$\Rightarrow$By taking $U_{1}$=$U_{2}$=$U$, then:
$\vert(\lbrack B_{t}U\rbrack Q^{\ast})(S,A)-(\lbrack B_{t}U\rbrack Q)(S,A)\vert$
=$Q^{\ast}(S,A)$
$\;\;$+$\alpha_{t}\cdot(R(S,A)+\gamma\cdot\sum_{S’}P(S’\vert S,A)$
$\;\;\;\;\cdot max_{A’}Q^{\ast}(S’,A)-Q^{\ast}(S,A))$
-$\lbrack Q(S,A)$
$\;\;$+$\alpha_{t}\cdot(R(S,A)+\gamma\cdot\sum_{S’}P(S’\vert S,A)$
$\;\;\;\;\cdot max_{A’}Q(S’,A)-Q(S,A))\rbrack$
=$Q^{\ast}(S,A)-Q(S,A)$
+$\alpha_{t}\cdot\lbrack\gamma\cdot\sum_{S’}P(S’\vert S,A)$
$\;\;\cdot(max_{A’}Q^{\ast}(S’,A)-max_{A’}Q(S’,A))$
$\;\;\;\;$-$(Q^{\ast}(S,A)-Q(S,A))\rbrack$
=$(1-\alpha_{t})(Q^{\ast}(S,A)-Q(S,A))$
+$\alpha_{t}\cdot\lbrack\gamma\cdot\sum_{S’}P(S’\vert S,A)$
$\;\;\cdot(max_{A’}Q^{\ast}(S’,A)-max_{A’}Q(S’,A))\rbrack$…[C]
$\leq(1-\alpha_{t})(Q^{\ast}(S,A)-Q(S,A))$
$\;\;+\alpha_{t}\cdot\gamma\cdot(max_{A’}Q^{\ast}(S’,A)-max_{A’}Q(S’,A))$…[D]
$\Rightarrow$Suppose we are under the definition $Q^{\ast}$=$BQ^{\ast}$ and $Q_{t+1}$=$\lbrack B_{t}Q_{t}\rbrack Q_{t}$, after contiguous running over some horizon:
➀the $Q$-learning just converges to have $Q\rightarrow Q^{\ast}$. The 1st part in [D] could be safely tossed out,it is becoming $0$.
➁the second part in [D] is saved, since it focuses on the $Q^{\ast}(S’,A’)$ and $Q(S’,A’)$ with $A’$ that can maximize the $Q$ value, by tossinig out averaging probabilistic transition from $S$ to $S’$ in [C].
$\Rightarrow$We now have the inequality below:
$\leq\alpha_{t}\cdot\gamma\cdot(max_{A’}Q^{\ast}(S’,A’)-max_{A’}Q(S’,A’))$
=$\alpha_{t}\cdot\gamma\cdot max_{A’}(Q^{\ast}(S’,A’)-Q(S’,A’))$…[E]
$\leq\alpha_{t}\cdot\gamma\cdot\vert Q^{\ast}(S,A)-Q(S,A)\vert$…for $S’$ is next state of $S$, we have $Q(S’,A’)\subseteq Q(S,A)$, this inequality just holds.
The Convergence Property 3
This 3rd property guarantees it converges.
➀$\sum\alpha_{t}\rightarrow\infty$
➁$\sum\alpha_{t}^{2}<\infty$
Could be found in Temporal Difference Learning - Part 1.
Addendum
➀Convergence-1, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
➁Convergence-2, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
➂Convergence theorem explained-1, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)
➃Convergence theorem explained-2, Charles IsBell, Michael Littman, Reinforcement Learning By Georgia Tech(CS8803)